基于全支付拍卖模型的众包激励策略优化分析

卢新元，郑雅婷，卢 泉，黄梦梅

(华中师范大学 信息管理学院，湖北 武汉 430079)

0 引言及问题提出

众包(Crowdsourcing)[1]伴随着互联网的发展而兴起，作为一种通过重新整合社会资源而形成的解决问题的方式，利用外部群体的创造性帮助企业以更高的效率和创意应对不擅长的领域与问题。Le[2]根据受托方完成任务获取奖励的不同将众包分成两类：一是基于接包方合作的协作式众包。二是基于接包方相互竞争，择优录用的众包竞赛。两种模式没有优劣之分，发布任务的组织或个人会根据不同的需求进行选择：(1)众包竞赛常被用作获取关键性创新解决方案或发布创意类任务的方式，此类任务的接包方通常是具有较高能力水平的专业人员(2)协作式众包则更多被用于降低成本，解决数据采集、图像标注等较易做到的简单任务，因此接包方主要是以时间换报酬的非专业人员。采用协作式众包模式的发包方关注的是，如何最大化利用众包获取全部接包方的总贡献；而采用众包竞赛模式的发包方只关心是否能够通过众包竞赛产出最优产品、服务与方案等。针对不同的众包模式采取具有针对性的激励策略是众包任务成功的关键[3]。

全支付拍卖模型由于要求参与者在未获知自己是否中标前就支付一定的不可逆投入，因此常应用于研究竞赛性质的博弈问题[4～7]。该模型在众包模式中的应用体现在无论接包方是否中标，所有参与该众包任务的接包方都需提前投入时间、精力等不可逆成本去完成众包任务。全支付拍卖模型已被广泛应用于研究众包激励相关问题。Chawla等[8]讨论了如何将全支付拍卖模型应用于众包问题，以获取最优的解决方案。在参与者为风险中性且处于信息对称的条件下，Matros[9]证明了将唯一奖励给赢者对期望获得最优方案的发包方来说是最佳的奖励策略。Terwiesch等[10]的研究表明不同类型的开放式众包项目的奖励策略不同，具体说来，知识共享类别的众包任务中设置最终奖励个数不唯一(即多奖元组)的激励策略能很好地提高接包方接包的积极性，而创意型众包任务奖励中发包方获取最佳方案的奖励策略是仅奖励唯一胜出者(该策略还有利于激励高水平接包方参与接包)。鉴于宽松、温和的奖励制度会减缓创新型众包活动的创新竞赛过程，甚至使该过程停滞并最终浪费奖励资源，Denicolò[11]研究表明赢家通吃的奖励策略在高度创新的众包活动中激励效果更好。Moldovanu和Sela[12]认为在有奖励预算的控制且满足线性努力成本函数的情况下，无论是追求接包方贡献总收益最多还是追求接包方贡献最高质量收益最多，赢者通吃都作为最优的激励策略。但也有学者认为在众包竞赛过程中，多奖元组模式优于唯一赢者模式。Cason[13]等通过实验发现设置多个奖励对参与者更具吸引力，更能提高众包竞赛的创新绩效。Luo[14]考虑到未知类型的随机用户和具有厌恶风险存在的用户，从发包方利润最大化视角设计了基于多奖元组为奖励策略的优化模型，并且验证了众包活动中多奖元组的激励策略优于固定奖励的激励策略。Cavallo[15]等认为给所有事实上提交贡献了解决方案的参与者支付报酬是比只向最优方案提供者一人给予奖励更有效的方式。Duffy[16]认为基于总体奖励金额一定，且假定所有参与者付出努力均高于其获得报酬的情况下，采用图洛克拍卖模型(Tullock Lottery)会使得接包方贡献总收益高于采用全支付拍卖竞赛模型。他进一步提醒到，总体奖励的预算限制实质上要求发包方在奖励数量与单个奖励价值之间进行取舍。Liu等[17]研究发现在类似协作式众包模式中，当总体奖励固定时，按照参与者的实际努力效用函数高低进行奖励分配可使得接包方贡献总收益最高。国内学者夏晓华和王美金[18]基于全支付拍卖模型的研究表明，当非对称竞赛活动的参与者实际水平时高于其在竞赛中的努力水平时，线性奖励策略在非对称竞赛活动中的激励效果不如固定奖励策略；然而当所有参与者都付出全部努力时，固定奖励策略的激励效果不如线性奖励策略。

综上所述，已有众包激励策略的研究侧重在有奖励预算限制的条件下采用竞赛模型优化激励策略，较少从协作式众包以及众包竞赛两种不同众包模式下，考虑众包激励优化问题。因此，本研究从奖励数量最优设计的角度出发，基于拍卖理论，考虑众包场景中参与者多样化的背景和能力水平，分别对两种众包模式进行建模，研究了以接包方贡献总收益最大化和接包方贡献最高质量收益最大化为目的的众包奖励分配策略。最后通过比较静态均衡分析及数值算例验证，对不同目的下众包奖励分配策略优化模型进行论证。

1 问题描述及模型建立

本文参照郑雅婷学位论文中的相关设置[3]，采用全支付拍卖模型研究众包模式中奖励数量如何影响接包方收益。本文模型假设是单一发起方(发包方)，多个竞拍方(接包方)的单一阶段的全支付拍卖，接包方行为遵循理性人假设，且每个接包方的出价不受其他人影响。基于全支付拍卖模型的众包活动参与者对照如表1所示：

表1 众包过程与全支付拍卖过程中的术语对照

模型参数设定如下：

(1)接包方的风险偏好类型为风险中性，且对于任务报酬的感知只与自身努力程度相关，不受其他接包方影响。拍卖中，有n个(n≥1)接包方同时(单一阶段)竞争S个(S≤n)单个奖励价值为V的同质奖励。

(2)拍卖为不完全信息环境，接包方对竞争者的能力不完全了解。即接包方整体的能力分布函数F为公有信息，而具体每一个接包方个人的能力水平vi为私有信息，每个接包方只了解自己的能力信息。

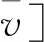
由此得，接包方的均衡策略为:

(1)

而排在第s位的接包方的能力概率分布函数为：

(2)

根据以上分析，考虑到两种不同众包模式中发包方所关心的期望收益不同，以下分别对协作式众包模式中接包方贡献总收益，以及众包竞赛中接包方贡献最高质量收益进行建模。

1.1 协作式众包模式中的接包方贡献总收益模型

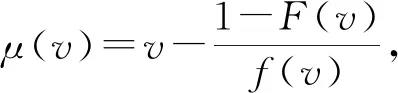
(3)

为了方便起见，使用v(s,n)来表示参与众包活动的接包方可以获得本次活动奖励的概率排序，F(s,n)为v(s,n)的累积分布函数，则接包方贡献总收益函数为：

(4)

1.2 众包竞赛中的接包方贡献最高质量收益模型

(5)

如何最大化获取接包方贡献总收益以及接包方贡献最高质量收益，是本文关注的主要问题。本文针对两种不同众包模式中的期望收益设计了不同的最优奖励分配策略。并讨论了接包方参与者数量及能力对最优奖励策略的影响。针对以上问题，本文在第三节及第四节展开了具体的研究，并对相关结果进行了数值算例验证分析。

2 众包激励策略优化分析

2.1 接包方接包策略分析

首先需要研究设置的奖励个数如何影响接包方的接包策略。假定能力系数k为1不变，接包方人数设置为100，奖励数量分别为30，50，80时的接包方参与策略如图1所示，我们可以发现接包方会随着奖励个数的增加而增加其参与。

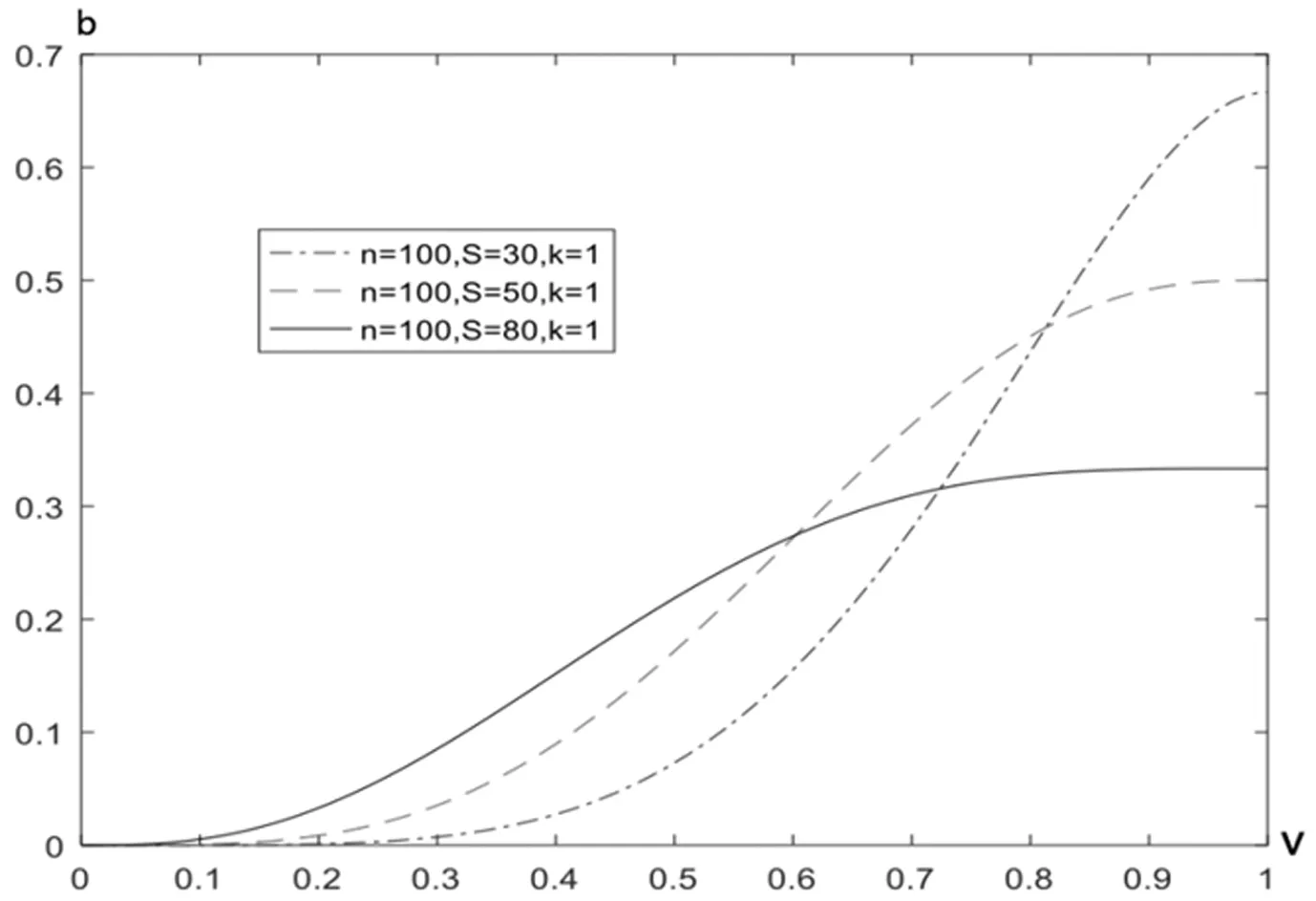
图1 奖励个数与接包方参与策略关系

接下来从数理模型对以上结论进行验证。

2.2 发包方激励策略优化分析

1)以接包方贡献总收益最大化为目标的最优奖励分配策略

高科技企业在机器学习、数据挖掘等方面存在大量数据收集和数据标注任务，发包方期望通过众包来获取更多的外部资源，即期望众包活动中总收益最大化[3]。本文接下来研究如何进行奖励分配以帮助发包方从众包中获取接包方贡献总收益最大化。

在公式(4)中，我们采用了μ(v(s,n)(v))指代奖励的边际效用。由于增加奖励个数对于接包方总收益的边际效用随着实际努力效用的不断增大而减小，且初始奖励的边际效用应为正数，则第n个奖励的边际效用需为负数。

①第s个奖励的边际效用函数严格单调递减。

②第一个奖励的边际效用为正。

③第n个奖励的边际效用为负。

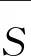
2)以接包方贡献最高质量收益最大化为目标的最优激励策略

企业采用众包模式寻求外部创新时，仅关注是否能够获取最优的创新方案，而并不关心整体方案提交数量及质量。本文接下来研究如何进行奖励分配以帮助发包方从众包竞赛中获取接包方贡献最高质量收益。

①第s个奖励的边际效用函数严格单调递减。

②第一个奖励的边际效用为正。

③第n个奖励的边际效用为负。

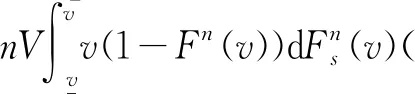
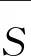
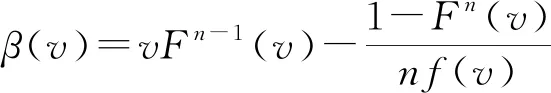
3 众包激励策略的比较静态均衡分析

从上文分析可知，在发包方无奖励预算约束时，可以通过多奖励分配策略满足两种收益最大化：发包方获得接包方贡献总收益最大化、接包方贡献最高质量收益最大化。接下来则是分析接包方的参与数量及能力水平如何影响最优奖励分配策略的选择。

3.1 接包方能力对最优奖励策略的影响

从(3)分析可知，当F(v)=vk，k>0，v∈[0,1]，且k取k1时，SP1是此时的最优奖励分配策略，且接包方贡献总收益P1的函数表达为:

当k取k2时，且k2>k1，若保持奖励分配策略继续为SP1，其接包方贡献总收益P2表达函数为:

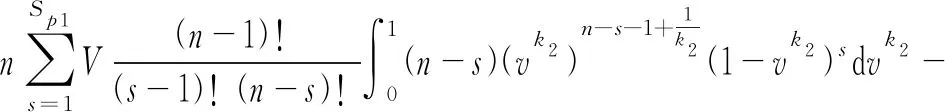
由于存在：

(6)

可知，当接包方能力提高到K2时，最优的奖励策略至少应为SP1不变，不能减少。

结论5在协作式众包模式中不设置奖励预算约束时，使得接包方贡献总收益取得最大值的最优奖励个数并不会随着接包方能力提高而减少。

同理可知，当F(v)=vk，k>0，v∈[0,1]，且k取k1时，此时的最优奖励分配策略为SH1，最高的期望努力为H1；当k取k2，且k2>k1时，若SH1不变，此时接包方的贡献总收益为p2。换言之，当k值从k1提升至k2时，最优奖励数量至少为SH1。

结论6在众包竞赛模式中不设置奖励预算约束时，使得接包方最高质量取得最大值的最优奖励个数也不会随着接包方能力水平的提高而减小。

图2 不同能力水平接包方参与下接包策略关系图

当众包活动中奖励个数S与接包方人数n固定不变时，能力值分别设置为1、1.3、1.6，此时的接包方参与策略如图2所示。由此可知，当接包方能力水平提高时，能力高的接包方参与积极性得到提升，在众包活动中付出比之前更多的努力。反之，对低水平接包方来说，其他竞争者的能力提高意味着自身获得报酬的几率减小，因此他们会减少自身的努力程度。

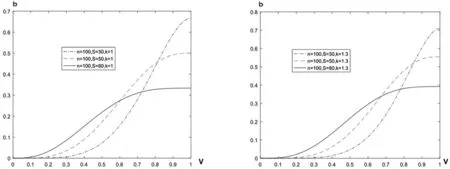
图3 接包方能力水平提高后其接包策略变化

分析图3可进一步得知，当接包方能力水平提高时，奖励数量增加带来的奖励边际效用也随之增加。当接包方能力由1提升为1.3时，能力水平较低的接包方会减少其努力程度。从公式(6)可知，第s个奖励的边际效用随着k的增加严格单调递增，即当接包方能力提高后，发包方为获取接包方贡献最大总收益，在设计奖励分配策略时应适当增加奖励的数量。

3.2 接包方数量对最优奖励策略的影响

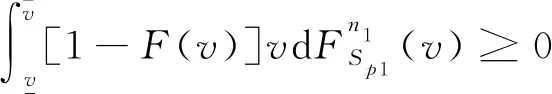
(1-F(v))Sp1-1F(v)n1-Sp1Fn2-n1(v)dF(v)≥0

(7)

结论7在不设置奖励预算约束时，使得接包方贡献总收益取得最大值的最优奖励个数不会随着接包方数量增大而降低。

结论8在不设置奖励预算约束时，使得接包方期望努力程度取得最大值的最优奖励个数不会随着接包方数量增大而降低。

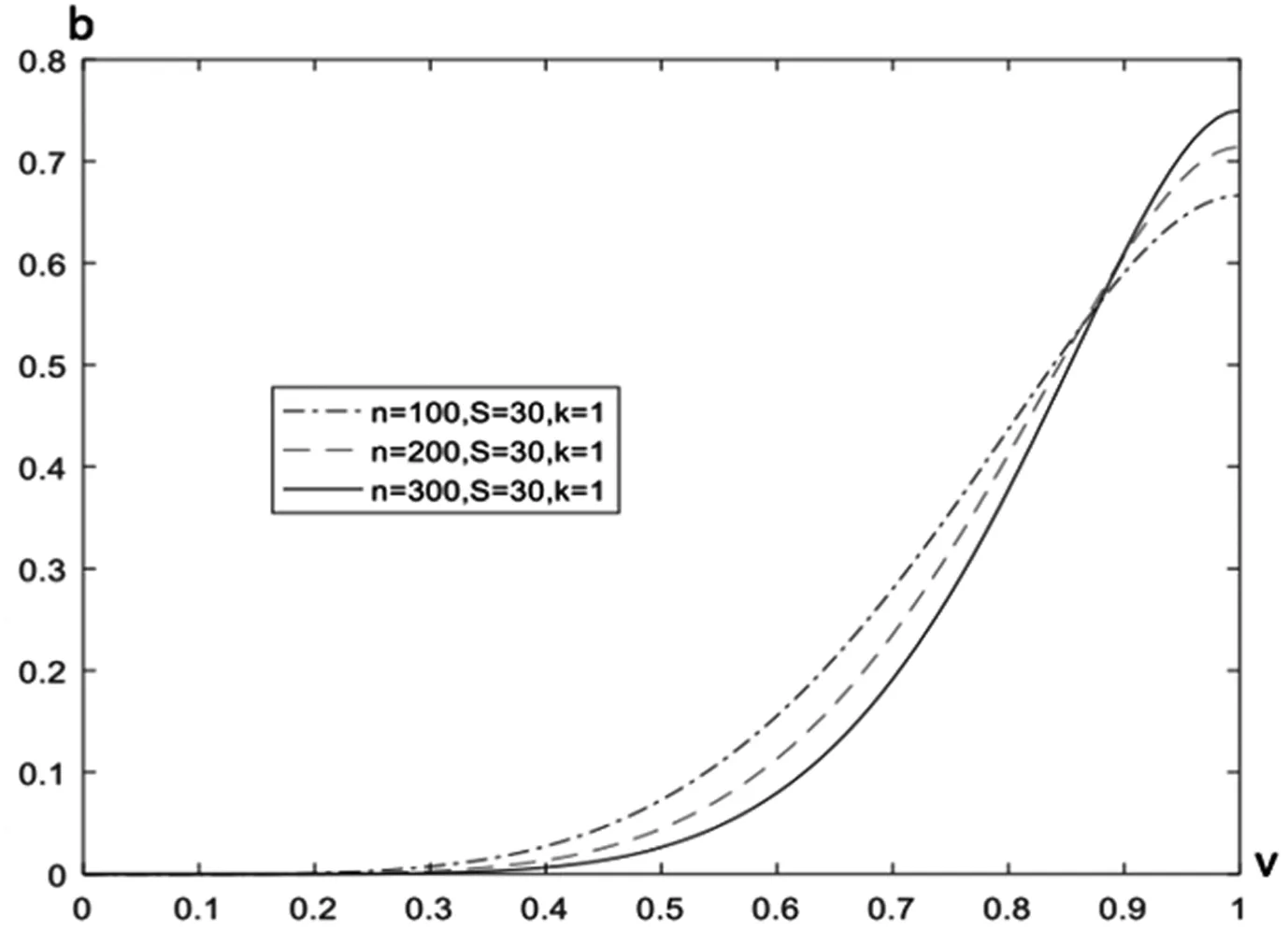
图4 接包方参与数量变化时接包策略关系图

当奖励分配个数与接包方能力值固定时，接包方数量n分别为100，200和300时的接包策略如图4所示。能力水平较低的接包方参与众包的意愿随着接包方参与数量的增大而降低。形成鲜明对比的是，水平较高的接包方参与意愿随着n的增大而显著增强。

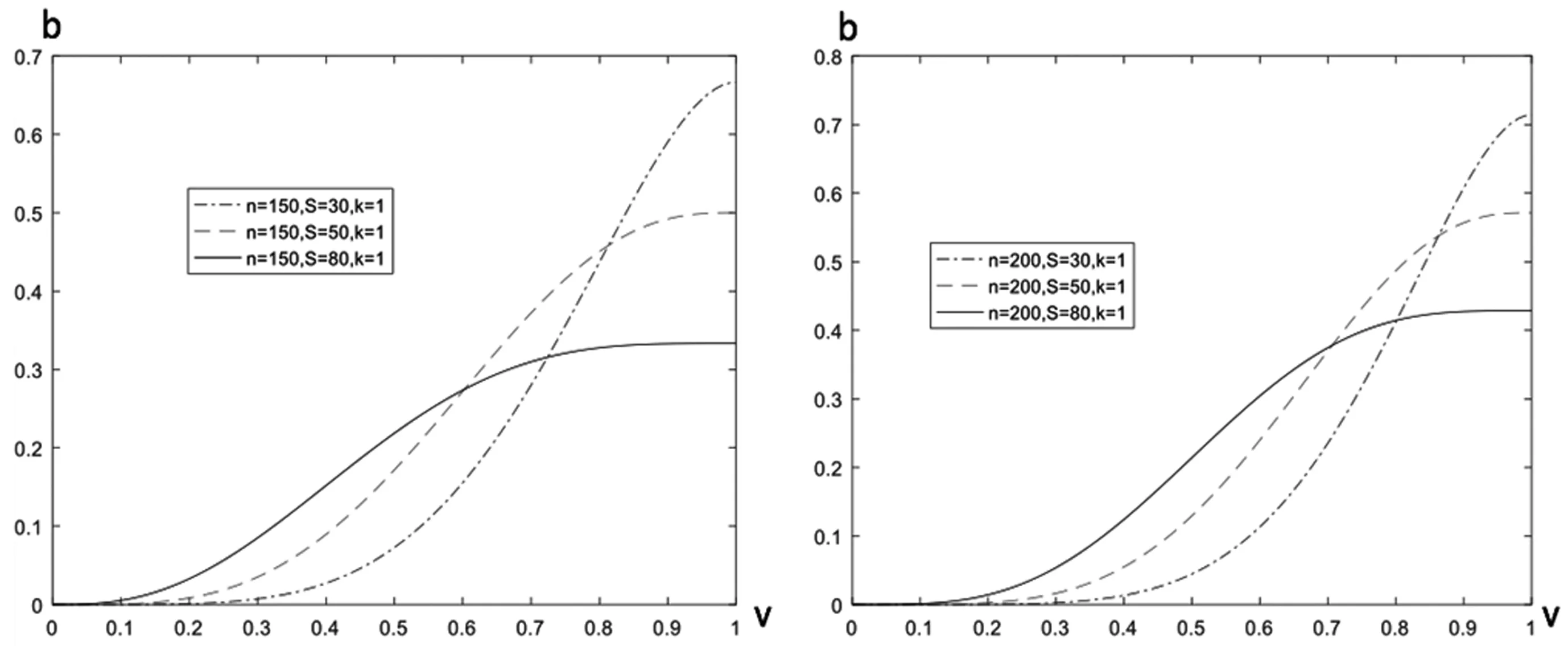
图5 接包方参与数量增加后其接包策略横向对比图

而如图5所示，保持奖励分配策略与发包方整体能力水平固定时，设定n由150增至200时，接包方均会随着参与数量的增加而提高其努力供给，与接包方能力水平无关。

4 研究结论与管理启示

4.1 研究结论

首先，本文将全支付拍卖模型引入到众包激励问题的研究中，考虑发包方不设置奖励预算限制的情形下，接包方与发包方的不完全信息博弈，分别对协作式众包与众包竞赛下的期望最高努力建立数学模型，接包方接包均衡策略的分析结果如下：

1)当奖励均质、无限制时，增加奖励分配数量可以作为提高能力水平较低的接包方参与意愿的激励方式。

2)与上述结论相反的是，奖励数量从S增加到S+1的过程中，增加奖励分配数量对高水平接包方的参与意愿具有负向作用。

其次，本文从协作式众包中接包方贡献总收益最大化和众包竞赛中期望最高努力最大化两个角度对最优奖励分配策略进行了分析。研究发现：

1)最大接包方贡献总收益函数与最大接包方贡献最高质量收益函数均为单峰函数。

2)在不设置奖励预算约束时，协作式众包中，使得接包方贡献总收益最大化的最优奖励分配策略为SP；而众包竞赛中，使得接包方贡献最高质量收益最大化的最优奖励分配策略为SH。

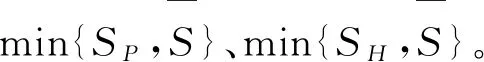
最后，采用比较静态均衡法分析了接包方数量和能力在两种众包模式中对激励策略的不同影响，结果显示：当接包方参与数量及能力水平提高时，发包方应增加奖励分配个数，以获取接包方贡献总收益与接包方贡献最高质量收益的最大。

4.2 管理启示

以往研究表明，在有奖励限制的条件下，众包竞赛模式中奖励分配策略固定时，发包方获取的接包方贡献最高质量收益为最优。本文建立了无奖励限制条件的情况下，在协作式众包及众包竞赛模式中，有助于了解发包方与接包方能力水平、参与数量、接包方贡献总收益与接包方贡献最高质量收益与奖励分配策略之间关系的模型。模型的结论给相关众包激励研究和实践带来一些启示：

1)结论1～4表明，奖励均质的情况下，多奖励分配策略能够使发包方获得最优接包方贡献最高质量收益和最优接包方贡献总收益。那么对于均质奖励的众包激励而言，需要设置多个奖励而并非采用赢者通吃的方式来激励众包的参与者。这个结论启示我们，在设置众包声誉激励奖励时(例如在众包平台授予的奖章、名誉、徽章等)，为了获取更多的参与者参与，或者激励优秀参与者参与，设置名誉奖励时，奖励个数不能唯一，需采用多奖励策略对参与者进行激励。

2)鉴于当奖励均质、无限制时，增加奖励分配数量可以作为提高能力水平较低的接包方参与意愿的激励方式。然而，增加奖励个数在正向激励低水平接包方的同时会负向激励高水平接包方；总体看来，对低能力接包者的正向激励作用大于对高能力接包者的负向作用。因此，发包方应当根据其选择的不同众包模式和预估接包方对于众包项目支持能力确定奖励分配比率，避免设置过多奖励限制了高能力接包方参与或奖励太少难以激励低能力接包方参与，以保证接包方贡献最高质量收益及接包方贡献总收益的优化。

3)发包方应当根据自身选择的众包模式特点选择能力相匹配的接包群体，即根据众包项目需要选择合适的第三方众包平台或选择自有平台以寻求更丰厚的期望收益。结论5～6启示我们，在无奖励预算约束的情况下，当明确了解到参与接包方整体能力水平提高时，设置更多的激励意味着更高的期望收益。不过，在真实的众包竞赛中，尽管在无奖励限制的情况下，更多的奖励分配意味着更高的接包方贡献最高质量收益，但由于众包竞赛的目的是为了获取少量而优质的方案，发包方在激励策略的选择上需要更注意奖励质量是否足够吸引高技术水平接包方参与。而结论7～8启示我们，为了使发包方获取最优的收益，当参与接包的人数增加时，奖励的个数也应当随之增加。