关于“评测指标权重确定的结构熵权法”的注记
肖枝洪,王一超
(重庆理工大学 理学院,重庆 400054)
0 引言
在系统测评指标体系时,由于每个测评指标与同类其他指标相比,其地位、作用和影响力不会完全相同,甚至差异很大,因此其重要程度就会不一样。因而在同时使用这些指标时,必须根据每个指标的重要程度赋予不同的权重,用指标的权重来刻画此指标对系统的贡献度。为此,确定指标的权重就成为关键问题。目前关于指标权重的确定方法很多,一般根据计算权重时原始数据的来源不同,可以将这些方法分为三类:主观赋权法、客观赋权法、组合赋权法。众所周知,由于主观赋权法和客观赋权法各有优缺点,所以很多学者致力于创新各种组合赋权法来改进上述二者,其中程启月[1]提出了结构熵权法来改进主观赋权法和客观赋权法。该方法首先将德尔斐专家调查法与模糊分析法相结合,形成“典型排序”,这是主观赋权法;然后运用信息论中的熵值法[2],对前述方法的无序程度或者不确定性进行度量;再以此为依据进行“盲度”分析并扫盲,从而达到改进指标权重的目的,使指标权重趋于合理真实。这个方法不仅具有较强的理论依据,还具有很强的可操作性,因而很多文献利用该方法来解决实际问题。例如,卢锦玲等[3]运用结构熵权法确定双重电压稳定指标的权重系数,从而评估大规模风电场接入电网后系统静态电压的稳定性。Fang Liu等[4]运用结构熵权法建立了针对大型商业建筑火险的评估系统,得到相应的火灾风险等级得分。Shengzhi Huang等[5]应用结构熵权法对植被指数各个指标的权重系数计算,提出了一个组合的NDVI预测模型,指导区域生态修复和环境管理。曾瑛[6]根据专家库的专家对电力ICT通信网各个环节单元的评价,利用结构熵权法对这些评价结果进行权重计算,综合所得各个环节单元的权重结果得出ICT电力通信网可靠性的综合评估指数。Zhao Xu[7]等根据专家意见的Delphi调查和模糊分析,然后根据给定的公式计算典型排序的熵值,分析盲目性,处理数据潜在的差异,为教学管理部门提供了客观有效的评估指标。上述文献都是直接运用结构熵权法解决实际问题。
对于分层指标问题,有些学者将德尔斐专家调查法与层次分析法进行结合得到主观赋权,再用结构熵权法对该主观赋权进行改进。例如,苏旭东[8]首先运用层次分析得到供应商柔性和资源整合柔性的德尔斐专家调查法的主观赋权,然后将结构熵权法与模糊综合评价法结合改进指标赋权,构建供应链柔性综合评价指标体系。魏道江[9]利用层次分析法从知识存量、知识价值、知识共享3个维度拟定一个包括3个一级指标、9 个二级指标的专家评选指标体系,并得到各指标的德尔斐专家调查法的主观赋权;再运用结构熵权法改进各指标的权重,提出一套在建筑企业内部评选知识专家的方法。邓红雷[10]也是首先运用层次分析法,将指标进行分层处理,得到气象灾害对架空输电线路的德尔斐专家调查法的主观赋权,然后再运用结构熵权法改进评估各气象灾害对架空输电线路的影响程度。盖奇文[11]运用层次分析法将公共图书馆展览绩效评价指标分为三级,得到各指标的德尔斐专家调查法的主观赋权,然后再运用结构熵权法改进其权重,建立了公共图书馆展览绩效评价指标体系。肖枝洪等[12]通过结构熵权法确定出每个房地产风险指标的风险水平,构建了房地产风险预警系统。孙雅茹[13]首先运用层次分析法对水资源、社会、经济和生态环境几个方面进行指标分级,并得到各指标的德尔斐专家调查法的主观赋权,然后运用结构熵权法改进指标权重,建立了长江下游水资源承载力评价指标体系。
也有学者根据实际问题,对结构熵权法进行了一定改进。例如,李仕峰[14]基于证据理论“可信度”和“确定性”,结合德尔斐专家调查法,构造了模糊评价矩阵,得到指标权重,改进了结构熵权法,并用于对NPD项目的复杂性进行模糊评价。董仲慧等[15]也运用证据理论对德尔斐专家调查法进行修正,修正专家的评判可信度,得到改进的结构熵权法并将之用于确定评估指标的权重,形成产品质量控制决策。徐浩[16]针对防空反导目标威胁评估指标权重很难确定、威胁评估信息存在不确定性的问题,通过重新定义“平均认识度”和“认识盲度”,并采用区间数灰色聚类方法得到区间型指标值矩阵用于计算指标权重,得出了一种改进的结构熵权法。上述文献尽管采用了不同方法对结构熵权法进行了改进,但都增加了较为复杂的计算步骤,使模型复杂化,相对文献[1]来说,可操作性要差一些。
上述文献不管是直接运用结构熵权法,还是对之进行了适当改进,但都没有注意到结构熵权法在对“典型排序”进行盲度分析时将隶属函数χ(I)转化为u(I)时所存在的问题(在下一节将进行详细分析)。而这个问题是结构熵权法用于改进主观赋权法的关键所在。因此,本文将仍然依照文献[1]的思想,修正隶属函数χ(I)的转化形式,对其方法进行改进,构造科学合理的评测指标权重确定的结构熵权法,并用文献[1]的数据进行实证分析。
1 改进确定指标权重的“结构熵权法”
为了叙述方便,本文沿用文献[1]的记号。文献[1]中u(I)的解析式存在以下四个问题:
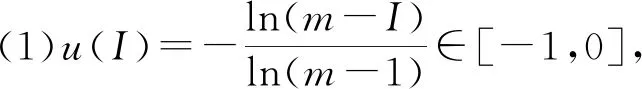
(2)专家zi对指标uj的认识盲度
Qj=|{[max(b1j,b2j,…,bkj)-bj]+
[min(b1j,b2j,…,bkj)-bj]}/2|
与j无关,也就是说,所有专家对指标u_j的认识盲度相同。如果是这样就没有必要用熵值法对主观法进行修正。
(3)隶属函数χ(I)与u(I)具有不同的函数特性。u(I)关于变量I为单调增函数,而χ(I)关于变量I为凸函数,如图1所示。按照文献[1]中取I=aij,对应的bij=u(aij)与aij的顺序实质上一样,没有起到任何调整作用。也就是说客观赋权法并没有对主观赋权法进行任何本质上的改进。

图1 隶属函数χ(I)与u(I)略图(m=15)
注:图1中取u(I)=ln(m-I)/ln(m-1)。与文献[1]中符号相反,所以图1中u(I)关于变量为单调下降函数。
(4)文献[1]所提及的Pn(I)意义不清晰,不知道是指概率函数还是其他什么函数有待商榷,同时它对由专家排序值aij推断定量转化值bij这一关键问题无任何作用。
由于上述问题,本文对确定指标权重的结构熵权法进行如下改进。
第一步,采集专家排序表,形成主观上的“典型排序”。
(1)根据“德尔斐专家调查法”原理,设计好《指标体系权重专家调查表》 。假设有n个指标uj,j=1,2,…,n,如表1所示,对此n个指标进行主观排序。

表1 测评指标排序表
注意:在表1中,专家认为最重要的指标排序为1,次重要的指标排序为2,依次类推。另外,如果专家认为某个指标与另一指标同等重要,可以排相同的序。
(2)根据“德尔斐专家调查法”的要求选取对测评指标熟悉、具有专业权威性、评价公正的k名专家,并让专家独立地对各个测评指标进行排序,其值记为aij,aij∈{1,2,…,n},i=1,2,…,k,j=1,2,…,n。
(3)将各个专家的排序表绘制成一张总表,在此,将最终形成的专家排序意见称为“典型排序”,见表2。
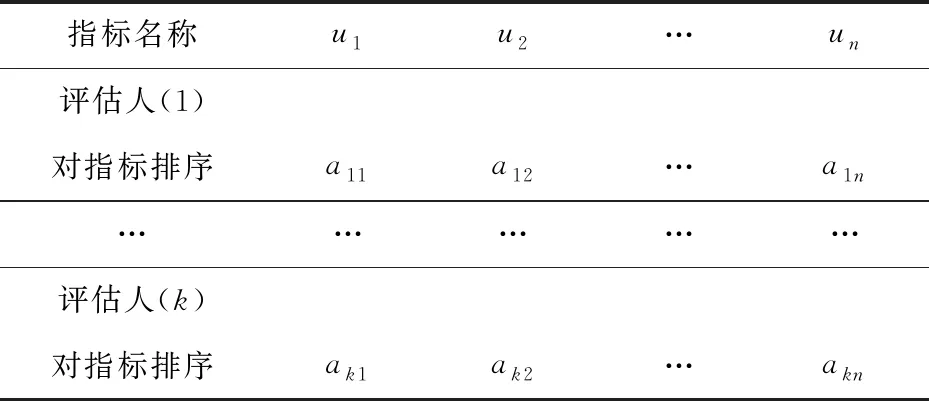
表2 典型排序表
第二步,对第一步获得的“典型排序表”进行盲度分析。
由于参加调查的专家可能存在个性差异,对指标的重要性理解存在偏差,其对指标的重要性排序可能会与真实的重要性顺序有偏差,从而产生数据上的噪声和不确定性,因此需要对典型排序表的结果进行修正处理,在此运用信息论中的熵权法来计算每个指标的熵值,减少专家排序的不确定性,使专家判断得出的各个指标的重要性趋于真实。
记指标集U={u1,u2,…,un},第i个专家给出的典型排序数组为{ai1,ai2,…,ain},根据信息论原理[2],对典型排序确定排序转化的隶属函数如下:
(1)
其中,I=1,2,…,n。
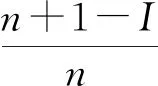



在式(1)中令I=aij,就可以得到bij=χ(aij),见表3。bij即为排序数I对应的隶属函数值,也就是不确定性。数组{1-b1j,…,1-bkj}视作k个专家对指标uj的话语权,对数组{b1j,…,bkj}取算术平均值,记作bj,称1-bj为k个专家对指标uj的一致看法,也叫作平均认识度。

表3 隶属度数据表
根据信息论中熵的定义,记k个专家对指标uj认知的不确定性为Qj,也称作认识盲度。其定义为:
Qj=max(b1j,b2j,…,bkj)
(2)
记k个专家对指标uj认知的整体认识度为,其定义为:
xj=(1-bj)(1-Qj)
(3)
其中,Qj如式(2)所定义。从而得到指标集U={u1,u2,…,un}改进后的结构熵权值X={x1,…,xn}。
注记4此处的Qj就是图1中xj曲线的下面部分,它刻画了专家对指标认识的盲度。而1-Qj就是曲线的上面部分,它刻画了专家对指标认识的一致性。bj是k个专家的平均认识盲度,1-bj就是k个专家的平均认识度。这一点与文献[1]中对bj的解释恰好相反,此处xj的定义也与文献[1]中xj的定义不同。
第三步,归一化处理。
记指标集U={u1,u2,…,un}中第j个指标uj的权重为αj,其定义如下:
(4)

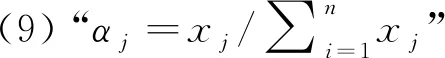
2 实证分析
本节针对文献[1]的环保项目测评数据进行分析。
首先,按照德尔斐调查法原理,计算指标的得分公式如下:
score=(100k1+75k2+50k3+35k4)/k
(5)
其中,k为专家总数,ki为将指标排序为i的专家数,i=1,2,3,4,k=k1+k2+k3+k4。如果认为该指标第一重要就打95分,第二重要就打75分,依次为55分和35分。由此也可以看出,这个打分也是具有很强的主观性。
根据式(5)计算出指标集U={u1,u2,u3,u4}各指标的得分为:
Score1=(95*2+75*1+55*0+35*0)/3=88.33
Score2=(95*1+75*2+55*0+35*0)/3=81.67
Score3=(95*0+75*0+55*2+35*1)/3=48.33
Score4=(95*0+75*0+55*1+35*2)/3=41.67
将上述各指标的得分进行归一化得到权重系数向量为:α=(0.3397,0.3141,0.1859,0.1603)。
其次,运用第二节的步骤确定指标集U={u1,u2,u3,u4}的权重。根据上述具体过程处理文献[1]的环保项目测评数据所得结果见表4。
从表4也看出,改进的结构熵权法将由典型排序法确定的指标权重进行了合理调整。对第一个指标的权重做了5.2%的调整,对第二个指标的权重做了5.4%的调整,对第三个指标的权重做了1.9%的调整,对第四个指标的权重做了13.51%的调整。

表4 环保测评指标典型排序的结构熵权计算一览表
注记6表4中指标u3与u4的权重相等,表面上看不合理,其本质是合理的。众所周知,在日常生活中或实际问题中,不太重要的指标人们往往不再注意区分,而对重要指标人们会集中注意力进行分析。

1-Q=(0.9769,0.9769,0.958,0.958)
X=(0.932,0.887,0.573,0.493)
α=(0.3223,0.307,0.199,0.171)
与文献[1]中表2对应的结果不同。
从此实例分析易知,“典型排序”是通过采用“德尔斐法”完成“专家意见形成—统计反馈—意见调整”,这样一个多次与专家交互的循环互动过程,充分发挥了信息反馈和信息控制的作用,给出的专家个体定性判断结果具有 “德尔斐法”意义的收敛性;而“改进的结构熵权法”采用熵理论建立模糊集的隶属函数,并进行认知“盲度”分析,又进一步剔除了专家在“典型排序”阶段对于因素认知上隐含的不确定性,能使专家意见趋于集中,这样就摒弃了“典型排序”定性分析中专家意见隐含“噪声”数据的弊端,更加使意见具有“一致性”收敛。
3 结论与讨论
3.1 讨论
虽然文献[1]的方法具有很好的创新性与可操作性,但其构建结构熵权法的隶属函数u(I)不具有信息论中熵的特性,也不是由熵的结论推导而来,这是其论文所提出新方法的关键点,所以本文基于文献[1]的思路,对其构建结构熵权法的隶属函数真正采用了熵的解析式,从而使专家的典型排序法确实得到了合理改进。
(1)本文在第二节所定义的隶属函数χ(I)在[0,1]上取值,其图形如图2所示。
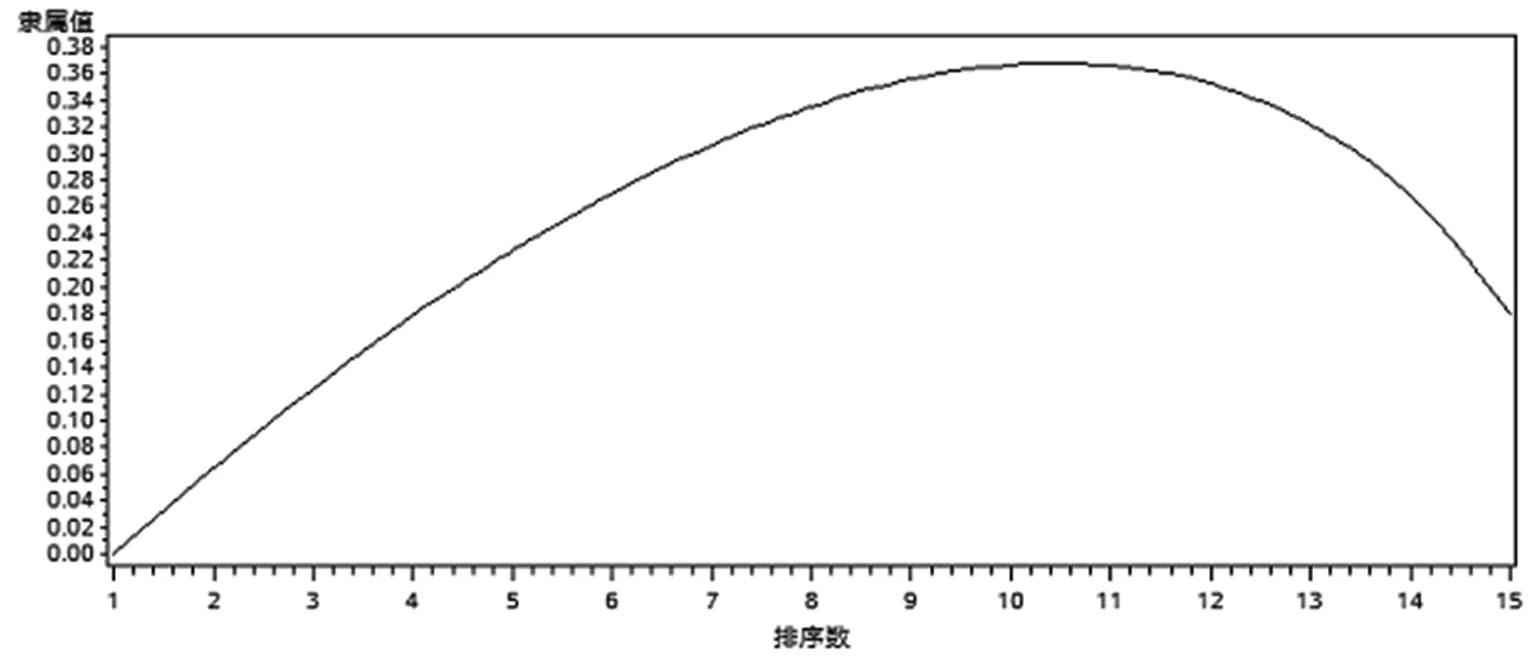
图2 隶属函数χ(I)示意图
图2的曲线为凸型,体现了熵的特点。位于图2中曲线下面部分为不确定性,也就是对指标认识的盲度;上面部分为对指标的认识度。这也说明了本文所定义的bj和Qj的合理性。
本文将经典的德尔斐调查法得到的指标权重向量与本文得到的权重向量进行了对比,并做出了合理解释。同时也指出了文献[1]中表2的Qj的计算并没有按照其给出的公式(7)进行计算。
(3)本文通过熵理论,借助德尔斐调查法得到的典型排序表,给出了专家对每个指标的盲度值和认识度,剔除了专家对指标的不确定性,并通过扫盲过程使专家对指标的重要性认识趋于一致。
3.2 结论
本文基于熵理论对专家集形成的“典型排序”、认知“意见”所产生的不确定性测量,通过建立模糊集上熵函数(隶属函数),并进行“认识盲度”分析,摒弃了专家在“典型排序”阶段认识上隐含的不确定性,并采用德尔斐专家调查法的多轮往复,能使专家意见趋于集中,完善群决策的一致性。此方法也为确定测评指标体系的权重提供了一种新的方法,通过计算公式的论证过程,可以看到这种方法的有效性和科学性。

