基于正交实验的轴承润滑参数确定

徐 鹏

（上海交通大学机械与动力工程学院，上海200240）

0 引言

现代实验方法（Modern Design of Experi-ment，MDOE）基于随机实验法和正交实验系统模型等方法。Ronald Fisher 基于传统实验方法发现采用随机实验法（即不按原有实验顺序）可以有助于发现系统误差来提高实验精度。这一发现被认为是传统实验方法与现代实验方法的分水岭［1］。而当实验次数太多时，可以从全部实验中挑选出一部分有代表性的水平组合进行实验，并对结果进行分析找出最优组合，这就是正交实验法的核心思想。与传统实验方法相比，现代实验方法通过随机实验识别系统误差，提高实验精度。采用正交系统模型的思想能避免资源浪费，提高实验效率，目前广泛应用于生物、数学和物理等领域。

现代实验设计一般包括以下5 种类型：（1）筛选设计，当研究因子个数在6～15个时，需要用筛选设计来确定对响应影响最大的2～5 个关键因子。这往往在对当前过程知识掌握程度较低时发生，一般通过筛选设计及实验后，还需进行过全因子或者半因子实验来确定关键因子。（2）因子设计，为了考察因素的主效应和感兴趣的交互作用，用各因素的全部或者部分处理进行实验，使得需要考虑的效应不被混杂的实验设计。因子设计包括单因子设计、全因子设计和部分因子设计。一般因子设计的因子为2～5 个。而部分因子设计中往往采用正交实验设计，通过挑选出部分有代表性的组合进行实验，这些有代表的点具有均匀性和整齐性。（3）响应曲面设计，利用多元二次回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优工艺参数，解决多变量问题的方法。一般响应曲面设计的因子为2～7个。（4）混料设计，调查的产品由多组分组成。例如，开发混合4 种化学成分的杀虫剂。在最简单的混料实验中，响应取决于这些成分的相对比例。相比较而言，因子设计中的响应则随每个因子的数量而变化。（5）田口设计，其宗旨是从产品的设计到制造过程中，通过控制源头的质量来抵御下游生产工艺波动或其他不可控因素的干扰，例如温湿度、材料老化及制造误差等。其设计重点在于最小化过程变异，或者使产品或过程对环境变化最不敏感［2］。

1 实际案例

1.1 主因筛选及水平确定

某线材公司生产用校直器轴承经常发生提前失效，导致产品缺陷率居高不下。针对该现象公司头脑风暴讨论列出以下8种潜在影响轴承失效的因素：轴承材料、润滑脂初始填充量、补充润滑周期、补充润滑脂填充量、润滑脂类型、载荷、轴承转速及轴承密封性。最终通过评估这些因素是否可以量化控制、控制难易度和控制方法筛选出主要因素为：润滑脂初始填充量（A）、补充润滑周期（B）、补充润滑填充量（C）和润滑脂类型（D）。主要因素的水平取值范围选择过程如下。

润滑脂初始填充量（A）：本例中润滑脂填充为在轴承侧填充，按经验公式在正常清洁状况下，润滑脂初始填充量为轴承座自由空间体积的40%。而在轴承工作转速低，且需要对污染进行有效防护时，需要填充100%轴承内自由空间体积的润滑脂。轴承内的自由空间体积计算公式如下。

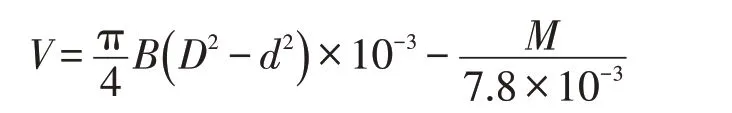
其中V为轴承内自由空间体积，B为轴承宽度，D为外径，d为内径，M为轴承质量。将轴承参数代入计算得出本例润滑脂初始填充量水平取值范围为2.7～3.0 g。

补充润滑周期（B）：SKF 为清洁工况下补充润滑周期提供经验查询表，在较严重的外界污染物下，SKF还给出对加脂周期tf的修正建议。计算方法为根据n·dm·bf及载荷比C/P值在经验图表中查询。其中，tf为补充润滑周期，n为轴承转速，dm为平均直径，bf取决于轴承类型和载荷条件的轴承系数，C/P 为载荷比。另外，SKF还建议了n·dm的限制值来提供最短的加脂周期建议。将本例轴承参数代入公式计算得出补充润滑周期的水平取值范围为2～7周。

补充润滑填充量（C）：补充润滑填充量公式如下。

其中Gp为补充润滑脂量，D 为轴承外径，B 为轴承宽度。将轴承参数代入计算得出补充润滑填充量为Gp=0.6 g。结合本例中加油枪的最小加脂量为0.2 g，补充润滑填充量的水平取值范围定为：0.2～1.0 g。

润滑脂类型（D）：润滑脂的选用需要考虑与轴承的实际运行速度相适应。从润滑脂选用建议手册中查询得知：通用型润滑脂D2 是符合要求的。而从公司实际出发，当前使用的润滑脂D1 为轴承的专用润滑脂，其价格比润滑脂D2 低近25%，如果D1 能够满足轴承润滑要求，为了便于润滑脂管理及减少维修成本，公司无须新增D2 型润滑脂。所以润滑脂类型水平为D1型和D2型。

1.2 选择正交表及正交表表头设计

常见的正交表有L4（23），L8（27），L16（215），L9（34），L27（313），L16（45）等。以L8（27）为例：L代表正交表，L下角的数字8表示有8横行，即需要做8次实验，括号内的数字2 表示因素有两个水平，括号内的数字7 表示有7 纵列，即最多允许安排的因素为7 个。本例中除了考察因素A、B、C、D 的影响外，还需考虑A 与B、A与C 的交互作用A×B，A×C。每个因素有两个水平，共4 个因素，每个因素的自由度为1。实验考虑两个交互作用，每个交互作用的自由度为1，所以总自由度为6，而根据正交表自由度大于等于各因素自由度和交互作用自由度之和，及选用最小号正交表的原则［3］，最终选择L8（27）正交表进行实验。可以看出正交表有以下两个特点：（1）每一列中，每一个因素的每个水平在实验总次数中出现的次数相等。（2）任意两个因子列的不同水平搭配出现的有序数列，每种数对出现的次数相等。所以正交表中的各因素水平组合在所有水平组合中的分布是均衡分散和整齐可比的。正交表表头设计中，对交互作用的分配需要按交互作用表进行分配，具体分配方式在论文中详细提及［3］。将各因素水平代码替换成具体的水平设定开始实验，实验安排及顺序如表1所示，实验结束将轴承失效个数填入表1中的结果列。

1.3 结果分析

对于实验结果的处理分析通常有两种方法，一是直观分析法，又叫极差分析法；另一种是方差分析法。下面用两种方法对比分析正交实验结果。

1.3.1 极差分析法

极差分析法的分析步骤如下：首先对每次实验各因素的水平一的实验结果计算出和的平均值k1。然后对每次实验各因素的水平二结果计算出和的平均值k2。再求出两水平和的平均值k1 与k2 的极差R，最后将R 由大到小排序以判断因素影响程度。极差分析结果如表1 所示。极差分析的判断原则为：极差越大，所对应的因素影响越重要。所以由上述极差排序可知各因素影响程度为B>C>A>D。另外，根据各因素水平所对应结果的平均值大小可以确定各因素的最优水平取值。如果指标期望越大越好，则取平均值越大的水平；如果期望指标越小越好，则取平均值越小的水平。由此可知，本例中的要求指标为越小越好，所以按极差分析法得出的最优水平为A2B1C2D2。

1.3.2 方差分析法

方差分析是用于区分所考察因子由于水平不同对应实验结果的差异是由于水平改变引起的还是由于实验误差引起的，以便进一步检验哪些因子对结果有影响，哪些没有影响，并区分哪些是主要因素，哪些是次要因素。方差分析法的分析步骤如下：首先列出各因子的自由度、交互作用的自由度、误差自由度和总自由度。然后求出上述各项对应的偏差平方和再通过偏差平方和除以自由度，求出各项对应的平均偏差平方和。然后根据平均偏差平方和除以误差的平均偏差平方和，求出各项对应的F值。最后通过F分布临界值表F（αf1，f2）查询得出对应各项的P值。其中，F分布临界值表中的横行f1代表各项因子的自由度fA，竖行f2代表误差的自由度f误。查到的临界值记作Fα，这里的α是预先给定的显著性水平，若因子的F值≥Fα，那么就有（1-α）的把握说明因子的水平改变对结果有显著性影响。一般常用的α值有α=0.01，α=0.05，α=0.10。当FA大于F0.01（f1，f2）时，说明该因子水平的改变对实验结果有高度显著影响，记作“***”；当FA值介于F0.01（f1，f2）与F0.05（f1，f2）之间时，说明该因子水平的改变对实验结果有显著影响，记作“**”；当FA值介于F0.10（f1，f2）与F0.05（f1，f2）之间时，说明该因子水平的改变对实验结果有一定影响，记作“*”。另外，对于影响不显著的交互作用，需要依次去掉（F值最小的）并入误差计算，然后再次进行方差分析，得出最终分析结果。正交实验的方差分析结果如表2所示。

表1 L8（27）正交实验表及实验结果

表2 正交实验的方差分析

根据方差分析法的结果可知，因素B的水平改变对实验结果有显著影响，因素C的水平改变对实验结果有显著影响，因素A的水平改变对实验结果有一定影响，因素D 的水平改变对实验结果没有影响，各因素影响程度为B>C>A>D。这样，直观分析法和极差分析法基本统一一致。

2 结语

在实际工作中会遇到很多参数优化的项目，如果用传统实验方法必将导致资源浪费，效率低下。而通过现代实验设计并且结合极差分析法与方差分析法来优化分析，能有效提高实验效率，节约成本。实验设计与数据分析是现代科学研究、产品质量优化中必不可少的一部分，所以掌握实验设计与相关分析方法至关重要。