初中几何教学“三步走”的教学模式

李林艳

摘 要：從新课改的思想来审视现在的初中数学教学，会发现其中存在着多方面的问题，本文试从教师及学生方面分析问题，结合笔者自身多年的教学经验，在教学中尝试了“分析思路——口述证明过程——书写证明过程”的几何教学模式，以如何提高数学课堂效率来谈谈自己的一些认识和思考。

关键词：几何教学 证明过程 课堂效率

数学教学活动中，特别是课堂教学应激发学生兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯，使学生掌握恰当的数学学习方法。 可见，如何使数学教学活动成为有效的教学已成为当前新课改下人们共同关注的一个话题。下面是笔者结合自己的教学实践谈谈具体的认识。

一、分析思路—引导学生学会思考

在几何教学中要特别关注学生分析问题的思路，教师要创设多种渠道，让学生的思想互相碰撞，从而归纳形成属于自己的思考模式。在这一环节中，教师只要精心地做一些引导，把更多的时间放手于学生，给予他们更广的空间进行思考。可采取小组交流合作的方式进行讨论，然后派一名代表上台讲解，若有不同意见或方法可自由发表，最后在方法上达成共识。这样不仅培养了学生的几何思维能力，同时也可鼓励学生对证明的问题进行大胆地质疑、猜想，甚至有一定的创新。

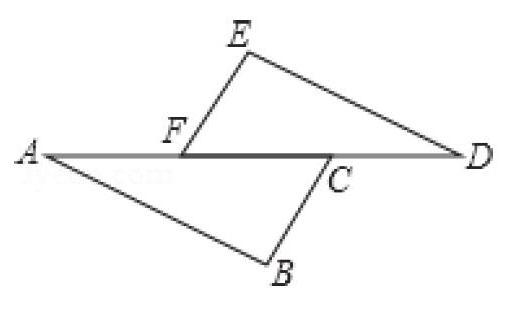
案例： （2012  衡阳）如图1，AF=DC，BC∥EF，请只补充一个条件，使得△ABC≌△DEF，并说明理由.

考点：全等三角形的判定。属于开放性题型，难度中等。

题目出示后，学生先是独立思考，而后迅速展开讨论。

学生1：这道题有很多种方法。

教师：能说出具体多到几种吗？

学生2：共有3种证明方法。分别可用SAS、ASA、AAS这三种判定方法来证明。（大部分同学赞同，只有少部分同学疑惑）

学生3：不对，应该有4种，除了SAS、ASA、AAS，还有SSS呢？

这时顿然引起了公愤：“错，题目中只知道一条边，而只能补充一个条件！”学生3恍然大悟，低声道：“噢，我知道错了！”

教师：很好，我们要提醒同学3认真审题哦！现在请各小组请一个代表上台来讲解一下吧。

学生4：我们添加的条件是EF=BC，利用SAS来判定△ABC≌△DEF。

学生5：我们补充∠A=∠D这个条件，用ASA判定△ABC≌△DEF。

学生6：添加∠B=∠E也可证明△ABC≌△DEF，判定方法是AAS。

教师：很不错，各组代表的讲解思路都很清晰，大家还要什么疑惑吗？

这时班上一个成绩基础较差的同学举手并站了起来：“老师，我们漏了一种方法，还有HL呢？”

很多同学嘲笑他：HL是用来证明直角三角形全等的！（不少同学还带有鄙视）

此时，这个同学的脸唰一下红了，显得有些胆怯。

教师：我们应该给他鼓掌，他能提出问题说明他是进步的，至少他在跟着我们大家的思路走。

… …

在教师的引导下，同学们顺利地完成了案例1的分析思路，不仅分享了他人的成果，同时也见证了平时解题过程中容易犯的错误。

二、口述证明过程—培养学生的说理能力

“说”一字在字典中意思解为用话来表达意思。本义为“释”，即为解释之意。《墨子·经上》解为：“说，所以明也”。《小取》中也有“以说出故”之说。认为“说”可以用来弄清一种事物形成的原因或一种主张所持的理由。语言是思维的工具，也是思维的结果。没有语言，思维很难实现。另一方面，语言的磨炼，也将促进思维更加清晰。俗话说，想得清才能说得明白。

笔者在这一环节中，重点解决以下三个问题。

1.树立每个学生敢于表达的信心

《课标》（2011年版）强调：“数学课程应致力于实现义务教育阶段的培养目标，要面向全体学生，适应学生个性发展的需要，使得：人人都能获得良好的数学教育，不同的人在数学上得到不同的发展。”在第一步的基础上，很多同学信心十足，让他们来说证明过程基本没问题，而恰好这样的机会会被程度好的学生“抢光” ，剩下的一部分学困生只能“干瞪眼”。于是，为了保证让每个同学都开口说话，笔者由传统的“单独提问”变成“大合唱”，来掩盖他们内心的自卑，很大程度上提高了每个同学的自信心，同时也给予了他们在课堂上应得到的尊重。

2.统一证明方法，达成共识

在几何教学中，一个命题的证明或是一道题的解法上往往会有很多种解法，

若不统一方法，学生各说各的，很难保证课堂的有效性。为此，我们在“大合唱”之前，要先做两个统一：一是方法;二是理清先后顺序，使思路更加清晰。对初学几何的学生来说，刚开始会有些不适应，甚至跟不上节奏，但只要教师多给予鼓励和肯定，他们很快就能进入状态。然后再由教师或一个“小指挥（学生）”通过图形来引导他们口述证明的过程。

3.教师点评，限时完成以保证课堂效率

教师应当及时点评，对出现的错误或不足要及时加予订正。除此以外，还要对他们的口述进行计时，一遍不行就两遍或三遍，直到完成目标为止。这样做不仅没有让他们觉得反感，反而让他们感到很刺激，高度集中了每个人的注意力，同时也培养了他们的团结合作精神。

三、书写证明过程——使问题落到实处

它是整个课堂教学中的一个重要环节，教师应该留给学生一定的时间来完成证明过程。学生可以采取自主书写或上台板书的形式，教师巡视时做些适当的辅导;而教师则可以通过投影设备来呈现学生易错点的共性或个性，以使课堂效率更具有效性。同时教师还需强调以下几点要求：

第一，要规范作图，必须用尺子、三角板、圆规、量角器等;

第二，对引用的数学公式、定理、概念、几何符号必须准确无误，如：∵（因为）、∴（所以）、对顶角相等、等量代换、SSS、SAS、ASA、AAS、HL 等;

第三，书写格式要规范，∵（因为）、∴（所以）各占一行，不能连着写，需注明的理由要加（……）

第四，在证明过程中表达的元素（边、角、顶点）必须要和图中的一致，如：图中标注的∠1、∠2、∠3……和证明过程中的表达要吻合。

参考文献：

[1]吴麦科.浅谈初中几何教学的问题与对策——以“全等三角形”为例[J].中学数学教学参考，2020（15）：9-11.

[2]杨红芳.失之东偶收之桑榆—谈模拟试卷讲评的做法和体会[J].中学数学教学参考：中旬，2013（5）：41.