基于改进颗粒模型的筒仓卸粮宏细观力学响应模拟研究

冯 永 潘 樊 刘 杰

(河南工业大学土木工程学院，郑州 450001)

筒仓在贮存散体物料方面具有容量大、占地面积小等优点而被广泛应用，其结构设计的关键在于对仓储工况荷载的正确把握[1, 2]。而相对于静态工况，粮食等散体物料在筒仓内的动态运动规律则更为复杂[3-8]，较多学者对此展开研究。

图1 颗粒接触模型

陈长冰等[9]用PFC2D中的等圆形单元模拟颗粒，研究了筒仓卸料过程中储料的流动状态、颗粒间接触力以及侧壁压力的变化。丁盛威等[10]运用PFC3D中的球形单元，分别对静态工况及动态工况的筒仓仓壁侧压力进行模拟分析，得出颗粒流动状态影响仓壁压力变化。有研究通过离散元模拟和室内实验分析了仓壁内部附着物对侧压力分布的影响，以及动态侧压力分布规律与物料流动状态，但其模拟所采用的颗粒接触仍是单一球单元的线性接触[11-14]。随着对侧压力研究的不断深入，不少学者提出筒仓成拱效应，有研究通过结拱时候的拱线分析,得出粮食速度骤降而产生惯性力进一步增大了仓壁侧压,并通过实验及数值模拟进行了验证分析，但所采用的的模拟单元依然是传统ball单元[4, 15-17]。已有报道虽然一定程度上推动了筒仓内颗粒流动模拟的研究，但其采用的模拟单元模型并不十分严谨，实际中在粮食周围存在的杂质及粉尘对颗粒流动及侧压力均有很大影响。现有研究采用的单一ball单元模型，简图如图1所示，由于颗粒粒径相同，颗粒在排列时空隙较大、挤压不充分，不能客观反映颗粒间及颗粒与仓壁间接触的实际情况，特别是颗粒-仓壁接触面积变小[18]，常导致数值模拟结果和实验结果不吻合。

本研究在单一ball单元离散元程序基础上，添加黏度系数较大的微型颗粒来模拟粉尘，旨在建立一种改进颗粒组构力学模型，并将该模型应用于筒仓卸粮模拟研究中。基于新旧模型的对比，对卸粮过程中散体动力学参数进行深入探究和分析，以期为改进模型、筒仓结构优化提供参考。

1 模型本构关系

1.1 传统ball单元模型与改进颗粒模型比较分析

根据离散元法[19]，传统ball单元模型采用单一圆形颗粒模拟粮食颗粒，颗粒单元用i表示，颗粒组构见图2a。基于目前传统ball单元颗粒模型的局限性，本研究的改进颗粒模型将传统ball单元颗粒改成2种大小不同的颗粒，新加入的颗粒单元模拟杂质用k表示，改进颗粒模型包括2种基本单元大球颗粒i和小球颗粒k，改进颗粒组构如图2b所示。

注：Kn为颗粒正向刚度/N/m；Ks为颗粒切向刚度/N/m；Tn为正向强度/N/m2；Ts为切向强度/N/m2；u为摩擦系数；i为大型颗粒单元体，k为小型颗粒单元体。图2 传统ball单元模型与改进颗粒模型

图2中的弹簧单元表示颗粒间接触前的线弹性行为，阻尼器单元用来产生能量耗散。颗粒间未接触时无作用力，用分离器单元来表示。颗粒切向接触的滑片单元遵循摩尔-库伦摩擦定律，切应力大小应由颗粒间的黏度系数与摩擦系数共同确定。

1.2 改进颗粒模型基本单元间接触关系

改进颗粒模型单元间的接触，包括颗粒-颗粒间的接触与颗粒-仓壁间的接触，2种接触情况计算可选用Lin等[20]提出的几何平均法，解出颗粒间或颗粒与仓壁间的接触点坐标，并将其转化成剪切力与位移关系曲线，颗粒与仓壁间接触关系如图3所示。

注：xci，yci；xck，yck为圆心坐标/mm；xc，yc为接触点坐标/mm；xcj，ycj为仓壁j起始坐标/mm；ri，rk为接触半径的向量/mm；θi，θk为角速度/rad/s；vxi、vyi，vxk、vyk为线速度为交点向量，αi、αk为与X轴夹角/rad，rw为接触半径的向量。图3 颗粒与仓壁接触示意图

假设坐标系中半径为ri的圆形颗粒i的圆心坐标为(xci，yci)，仓壁j的起始坐标为(xcj,ycj)，横轴与x轴的正向夹角为θi。圆形颗粒i的方程为：

(1)

若式(1)无解，则颗粒与仓壁间无接触；若有解，则证明颗粒与仓壁有接触，此解即为接触点坐标(xc，yc)。

基本的单元间力与位移的关系在已有工作中已经证明[21]，本研究不再赘述。

2 物理模型实验及离散元模型的建立

2.1 实验装置

为了观察筒仓内粮食颗粒的流动状态，采用亚克力材料制作模型筒仓仓壁，筒仓根据实际常用筒仓尺寸1/20的缩尺比例建立，仓壁高1 000 mm,直径为500 mm，仓壁厚度约为8 mm,漏斗半顶角为60°。按照等间距的原则在仓壁左右两侧布置监测点来检测筒仓卸粮过程中的侧压力。筒仓模型的具体尺寸和监测点布置如图4所示。

将实验模型仓内装满粒径为5～6 mm的小麦，通过室内实验测得实验小麦的具体参数，见表1，待装料稳定后获取筒仓静态侧压力，之后撤掉料斗底板进行卸粮实验获取动态侧压力，多次实验取其平均值。

表1 实验小麦参数

2.2 实验结果

筒仓卸粮实验进行中，由于颗粒初始流动速度较快，最上部监测点的数据差异性较大，故在数据提取处理时选取2、4、6、8，这4个监测点位的数据，通过采集的仓壁应力数据，整理得出仓壁侧压力随时间变化图，如图4所示。

图4 实验装置

由图5可以看出，随着卸料的进行，4个点位的侧压力曲线走向基本保持一致，仓壁压力随实践步长的增加逐渐趋向于零。仓壁的侧压力呈现不规律性的振荡，且越接近筒仓底部，仓壁侧压力振荡幅度越大。

图5 仓壁侧压力随时间变化图

2.3 离散元模型及参数的建立

为了深入探究改进模型在筒仓模拟研究中的应用优势，参照室内实验筒仓，建立同尺寸筒仓模型。

改进颗粒模型中加入体积更小但黏度更大的颗粒k，使i、k颗粒数量比为10∶1，用来模拟筒仓中粮食颗粒间的粉尘杂质。模拟的颗粒及模型时步参数如表2、表3所示。

表2 传统ball单元颗粒及改进后颗粒参数

表3 计算时步参数

2.4 验证模拟模型的合理性

筒仓静态侧压力的计算采用目前普遍应用的Janssen理论，计算公式为：

Ph=γρ(1-e-μks/ρ)/μ

(2)

k=1.1(1-sinφ)

(3)

式中：γ为储料的重力密度/kN/m3；ρ为筒仓水平净截面的水力半径/m；μ为储料与仓壁的摩擦系数；k为侧压力系数；s为储料顶面至所计算截面的距离/m；φ为储料的内摩擦角/°。

选取改进前、后模型仓壁右侧的静态储粮侧压力数据、物理实验的静态储粮侧压力数据、式(2)～式(3)计算的静态侧压力值绘成曲线图(图6)。结果显示，Janssen公式计算所得的静态侧压力曲线与实验状态下曲线基本吻合，图6b为两者的误差线，其中最大相对误差出现在1号点位处，为14.6%，7号点位的相对误差为10.1%，其余点位误差都低于9%。

采用Z-Score标准化对实验数据和2次模拟数据进行了无量纲处理，如图6c，模拟值与实验值整体契合度较好，其中3号点位处的偏差最大，传统模拟和改进模拟分别相对实验值偏离0.20、0.39个标准差，其余点位的偏离值均在0.18以内，与实验契合度高，可以验证模拟的合理性。

图6 仓壁静态侧压力对比图

3 仓壁压力数据分析

3.1 压力曲线趋势对比分析

筒仓在自由卸粮过程中，位于上部的10号监测点测得的动态侧压力曲线波动幅度较小，随着粮食的下卸迅速进入零压力阶段，故选取2、4、6、8这4个监测点的卸粮动态侧压力来进行数据分析。

图7为筒仓各监测点的动态侧压力模拟对比图，在卸粮过程中，仓壁各个监测点的动态侧压力均大于静止状态下的侧压力；随着颗粒的不断流出，各监测点的动态侧压力上下波动，且随着时步的增加，侧压力逐渐减小至零。

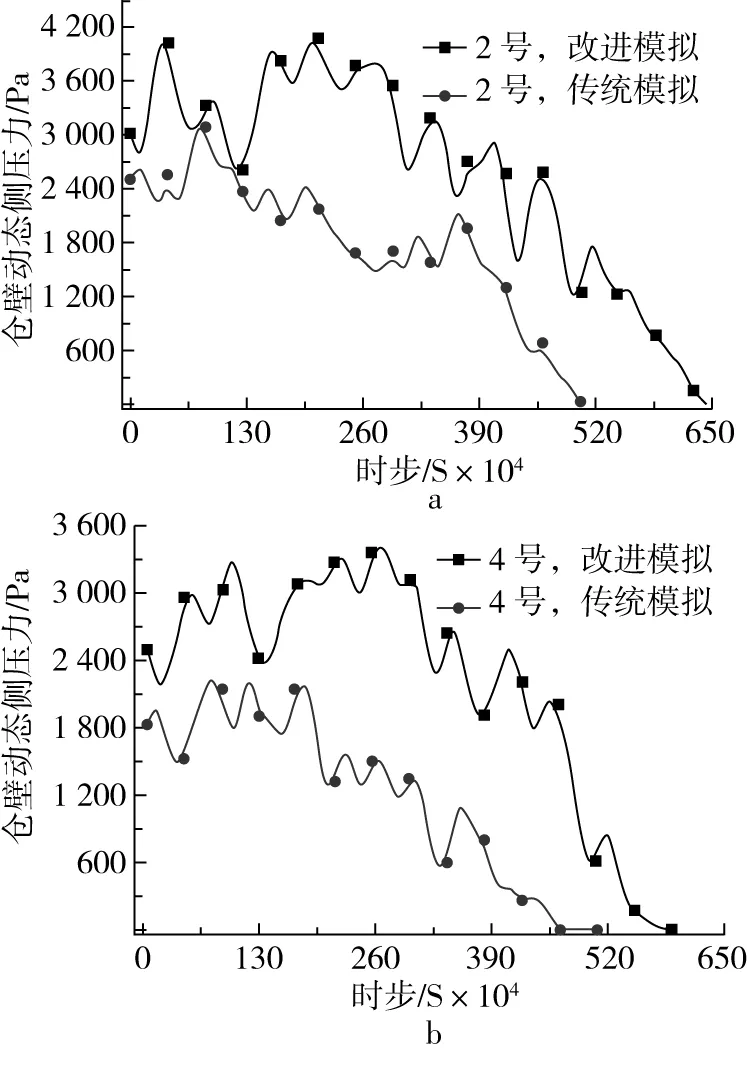
图7 各点位动态侧压力模拟对比图

对比图8中2种模拟结果可以发现，颗粒单元改进后卸料所需时步远远大于改进前。颗粒单元改进前的仓壁动态侧压力曲线波动幅度较小，各监测点处的压力曲线交叉较少；而改进后的模拟曲线波动幅度较大，各监测点处的侧压力曲线交叉较多。

图8 改进模型与传统模型仓壁动态侧压力整体对比图

其中，改进前，2号和8号监测点侧压力降为零的时步分别为252、17.5万步；2号监测点的最大侧压力在第105万步时为3 177 Pa，8号监测点的最大侧压力在第63万步时为1 415 Pa。改进后，2号和8号监测点处的侧压力减小为零的时步增加至644、420万步；2号监测点最大侧压力在第15.4万步时为4 364 Pa ；8号监测点处最大侧压力在第84万步时为2 292 Pa。相比改进前模型，2号和8号监测点时步数分别增加了155%和140%，终止时步数明显增大；最大侧压力分别增大了37.4%和62%，振荡的数值范围也变大。

主要原因是改进前的颗粒单元是单一球形颗粒，颗粒间空隙较大，接触挤压不充分又缺少黏结力，所以卸料过程比较顺畅，没有出现明显的压力成拱现象，即仓壁动态压力波动较小，各监测点压力曲线交叉较少且基本呈现出整体流动状态，直到颗粒完全流出，这一过程卸粮时间较短；改进后的模型添加了黏度大、直径小的圆形颗粒模拟粉尘，筒仓内颗粒分布更紧密，颗粒间的黏结、摩擦力使得颗粒下卸时出现压力拱，在仓壁处压力急速增大，随着颗粒的不断流动，压力拱被破坏，仓壁压力又迅速变小，周而复始的成拱-破拱使得仓壁侧压力上下波动且幅度较大。又因为压力拱在卸粮过程位置不断的变化，所以各个监测点处压力的数值都会很大，各点位的压力曲线交叉较多。同样基于此，仓壁两侧的颗粒流动受到阻塞，颗粒完全卸出用时较长。

3.2 数据准确性对比分析

粮食对仓壁的动态侧压力，可根据GB 50077—2017《钢筋混凝土筒仓设计标准》[22]进行计算。

Ph=Chγρ(1-e-μks/ρ/μ)

(4)

k=tan2(45°-φ/2)

(5)

式中：Ch为深仓贮料水平压力修正系数，根据GB 50077—2017《钢筋混凝土筒仓设计标准》计算:监测点距仓壁底部的深度h为0～0.66 m时，Ch=2；h=0.72时，Ch=1.82；h=0.81时，Ch=1.56；h=0.9，Ch=1.29。

图9 不同方法下测得的动态侧压力

图9为运用不同方法下的仓壁动态侧压力对比图。由规范计算公式得到的各测点动态侧压力随距仓底高度的增加呈现出平稳减小的趋势，且在下降过程中无波动。但实验数据和改进后的模拟曲线显示，在2号和4号点位处动态侧压力有向上波动的趋势，分别超出规范计算数值6.6%和4.1%，表明筒仓在卸粮过程中，在靠近筒仓底部1/3处有成拱效应，粮食在此处堆积导致仓壁动态侧压力较周围测点有明显的升高，这与张大英等[23]的研究结果相符。而其他监测点处的动态侧压力显然比规范计算值更大，这符合规范取值保守的原则，故改进后的模拟数据与实验数据更相符。

用改进前、后的动态侧压力和实验数据做对比，改进前的仓壁动态侧压力模拟值与实验值的相对误差较大，其绝对值在7.93%～30.06%之间；而改进后的仓壁动态侧压力模拟值与实验值吻合较好，相对误差绝对值在1.64%～10.93%之间。改进后各测点模拟曲线与计算曲线相对误差绝对值均小于11%，在合理范围，可以参考相近研究的误差范围[24]。以图8的数据曲线为标准值，利用式(6)求出改进前模型曲线的标准差为606.66 Pa，改进后颗粒模型曲线的标准差为137.50 Pa，比改进前模型减小了77.3%，与实验数据曲线更接近，拟合效果更好。

(6)

图10 模拟与实验过程中监测点切应力与位移关系曲线图

4 仓壁压力细观力学机理分析

在细观角度上，通过卸粮过程颗粒的力与位移的变化关系以及力链的构成，深入探究仓壁动态侧压力变化的机理。取改进前、后颗粒模型的2、4、6这3个监测点，做切应力与位移曲线对比图，如图10所示。传统ball单元模型在卸粮的过程中，切应力的增长相对缓慢，说明颗粒间黏结强度较低。而改进颗粒模型各监测点切应力迅速提高，并很快达到最大值，说明颗粒间黏结强度较高。取实验与模拟的6号监测点剪切力-位移曲线，以实验模型曲线为标准值，根据式(6)，得出传统ball单元模型曲线的标准差为100.1 kPa，改进颗粒模型曲线的标准差为87.5 kPa，比传统ball单元曲线标准差减小12.5%。改进颗粒模型所得数据与实验数据更接近。

传统ball单元模型与改进颗粒模型卸粮试样的接触力链图如图11所示，其中右侧放大部分较粗的线条为颗粒力的传递。

图11 接触力链图

由图11a可以看出，颗粒接触力方向多为竖直向下,很少出现水平力链，这是由于单一颗粒在筒仓卸料过程中颗粒与颗粒的摩擦，以及颗粒与仓壁的摩擦都不充分，无法形成拱效应，因此颗粒对仓壁的挤压程度轻，水平力链较少。在筒仓卸料过程中(图11b)，颗粒力的传递方向包括水平方向和竖直方向，且力链分叉现象明显,这是由于加入的小颗粒k使得大小颗粒受压后孔隙减小，颗粒排列更为密实，在卸料过程中，颗粒-颗粒、颗粒-仓壁间摩擦充分，在仓壁处出现拱效应，水平力大幅增加。

从细观角度来看，传统ball单元模型由于切应力提高较慢，颗粒内部结构应力在不断地调整，颗粒间摩擦力、黏聚力较小，卸粮过程比较顺畅，无法形成拱效应。而改进颗粒模型由于切应力迅速提高，颗粒之间的裂隙被压实，剪切带完全贯通，导致颗粒之间的黏聚力增加，摩擦更为充分，卸粮过程中出现拱效应，更符合实验过程。

5 结论

针对传统ball单元颗粒模型对筒仓卸粮模拟研究的局限性，本研究提出了改进颗粒本构模型的思想，并运用物理数学方法推导了模型的可行性。本研究基于改进模型思想，依托室内实验，通过离散元软件进行筒仓卸粮模拟，从宏细观角度分别对比验证了改进模拟相较于传统ball单元模型在模拟中的优势。结果表明，仓壁侧压力随着时步的进行逐渐减小至零；2号和10号监测点处相比于传统ball单元模型，改进颗粒模型的仓壁压力变至为零的时步增加了155%和140%，完全卸粮时间大幅增加，最大侧压力增大了37.4%和62%，振荡的数值范围更大。

以实验仓壁侧压力曲线为标准值，传统ball单元模型的侧压力曲线的标准差为606.66 Pa，改进颗粒模型曲线的标准差为137.50 Pa，相比减小77.3%，改进颗粒模型数据与实验数据更接近。

以实验剪切力-位移曲线为标准值，传统ball单元模型剪切力与位移曲线的标准差为100 kPa，改进颗粒模型的标准差为87.5 kPa，相比减小12.5%，拟合的效果更好。