基于主要海洋灾害因子的浙江北部海域三疣梭子蟹补充量预测分析

王迎宾，高 丽，孙 洁

（浙江海洋大学水产学院，浙江舟山 316022）

三疣梭子蟹Portunus trituberculatus，隶属甲壳动物亚门Crustecea、软甲纲Malacostraca、十足目Decapoda、梭子蟹科Portunidae，梭子蟹属，分布于印度以及西太平洋海域[1]。其对温度适应范围较广[2]，广泛分布于中国、朝鲜、日本等海域，有较高的经济价值。2010 年以前，浙江省三疣梭子蟹产量增减有所波动，然而2010 年以后，浙江海域三疣梭子蟹的产量逐年走高，年均增长达到近30%[3-4]。然而影响三疣梭子蟹的潜在因素有很多，并且随着捕捞努力的加大，其丰度自然也会发生变化[5-7]。近年来，产量增加应该与补充量有关，而除了增殖放流以外，气候和环境因子对补充量的影响也较大。尤其是海洋环境因子对资源补充量产生巨大影响。较好的预测补充量的变化是提高资源评估结果准确性的前提之一[8-9]。因此，开展三疣梭子蟹资源补充量和海洋灾害事件之间关系的分析，将有助于深入研究三疣梭子蟹产量变化的原因与机制。

目前，国外学者对于资源补充量与海洋灾害因子之间的关系开展了较多的研究。如2005 年，SAKURAMOTO[10]根据西北太平洋二月的北极涛动影响和海表温度作为环境因素，基于亲体补充量新概念建立了补充量资源预报模型。准确再现了虚拟种群分析估计中的补充量、产卵种群生物量、年生物量的值且较好地再现了亲体补充量关系中的变异模式。2007 年，FUNAMOTO[11]在海洋表面温度与日本北部海岸渔业资源亲体量与补充量关系时，利用Ricker 模型研究渔业资源的亲体量与补充量对模型是否具有强烈的密度依赖效应。HIROYUKI[12]曾在2010 年对日本大阪湾的三疣梭子蟹资源补充量与台风数量和溶解氧的关系进行研究。2014 年，SHIH Chia-Lung，et al[13]基于GAM 模型建立了北太平洋长鳍金枪鱼Thunnus alalunga补充量模型。在国内，邓景耀等学者开展了补充量模型的动态研究，其采用了Ricker 和Beverton-Holt 繁殖模型来描述渤海虾亲体-补充量之间的相关关系。2007 年，张利永[14]根据东海现状，研究了大规模赤潮对微型浮游动物群落结构产生的影响。2013 年，刘尊雷等[15]根据1992-2012 每年5-8 月长江径流量、海水表面温度、径向风强和海平面气压等水温环境因子，建立模型研究亲体-补充量预报模型。2014 年，汪金涛等[16]学者基于海表温度、海平面高度等海洋环境因子对东南太平洋茎柔鱼Dosidicus gigas 资源补充量的影响展开研究，从而建立起预报模型，而中国针对梭子蟹资源补充量变动与环境因子关系的研究探讨鲜有报道。

海洋灾害事件，主要包括台风、赤潮、风暴潮、厄尔尼诺、海平面上升、海洋污染等事件[17]。浙江沿海是中国赤潮发生最严重的海域，同时浙江省每年都会遭受不同程度的台风，可以引起海洋营养盐跨温跃层运输，增加初级生产力和新生产力，并且每隔3～5 a 就会遭受一次特大风暴潮灾害[18]。在研究Alice 台风对东海鲐鱼补充量影响认为，台风过境时使流场的混合和湍流加剧，使仔鱼的垂向随机游走加大，最终导致鱼卵仔鱼普遍向深水区移动[19]。厄尔尼诺是太平洋海域一种反常的自然现象，海水温度异常升高，近年来其对西北太平洋渔业资源的影响也越来越受到专家的关注[20]。同时，厄尔尼诺事件的强度越大对浙江省风水年的影响也越大[21]。海面高度距平也在一定程度上影响着海洋资源与环境，对海洋生物资源变动有着重要作用，也会影响某些定期溯河洄游习性生物的正常洄游[22-24]。浙江沿海是我国赤潮发生最严重的海域，同时长江径流为该海域带来了大量的营养盐，水质较清、透明度好、光照条件充足，随着4-5 月水温的升高，水质满足了各种浮游植物的生长需求[25]。因此，该研究选取了对浙江北部海域影响较大的几个因子（赤潮、台风、海面高度距平、风速）开展其对三疣梭子蟹补充资源量的预测模型研究，希望通过模型的建立找到能够较好预测三疣梭子蟹补充量的方法，从而为渔业捕捞提供合理指导。

1 材料与方法

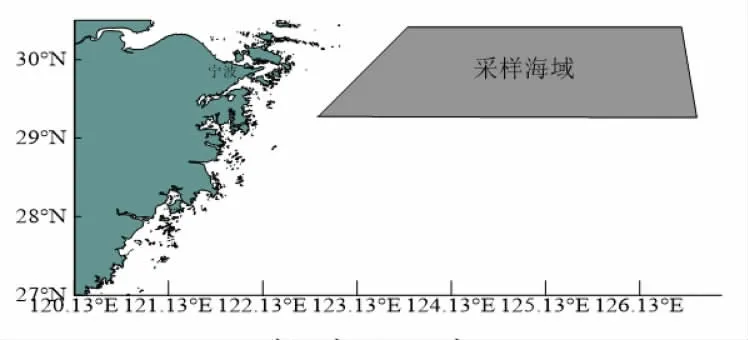
图1 三疣梭子蟹主要采样海域图Fig.1 Map of sampling area of P.trituberculatus

1.1 研究数据

1.1.1 生物学数据

2015 年5 月至2016 年5 月，在29.30°-30.50°N，122.48°-126.75° E 海域进行梭子蟹采样，采用渔具包括蟹笼、流刺网和单拖网。每月采集两次，一年内共获得三疣梭子蟹样品769 尾。研究所需生物学在实验室测定获得，包括甲宽、甲长、体质量和性别等，并根据甲宽对三疣梭子蟹进行分组。将3 种渔具采样获得的样品对其甲宽和体质量进行差异性显著检验，结果显示3 种渔具得到样品的甲宽和体质量差异均不显著（P＞0.05）。因此，该研究将不同渔具得到的三疣梭子蟹合并进行研究。

2001 年至2014 年浙江北部海域三疣梭子蟹渔获量从渔业管理部门获得。每年的资源量根据产量计算得到，所使用方程如下：

式中：N 表示资源量；Z 为总死亡系数；C 代表渔获量尾数；F 为捕捞死亡系数；M 为自然死亡系数；S表示选择率；L 代表甲宽组；a 为年份。

根据詹秉义[26]定义，补充群体为能够首次被渔具大量捕获的个体。前期调查发现，拖网渔船捕获的最小三疣梭子蟹甲宽约为60 mm。生物学观测实验显示，一般三疣梭子蟹在第8～9 次蜕壳后，甲宽范围在60～80 mm。因此，该研究将三疣梭子蟹补充群体定为甲宽在60～80 mm 的雌性群体。使用公式（1）得到每年资源量后，基于实验数据对资源量进行分组，可得到补充量的大小。总补充资源量根据历年产量和样品测定的甲宽频率结果推算得出。

根据相关渔业部门获取到了2011-2014 年的三疣梭子蟹放流量数据。近几年，中国三疣梭子蟹增殖放流量不断增加[27]，放流群体所也占到补充资源量的比例，为了剔除增殖放流三疣梭子蟹所产生的补充量的影响，使用公式（1）计算放流群体达到补充尺寸时的剩余的资源量作为放流三疣梭子蟹的补充量。由于2010 年以前浙江北部海域三疣梭子蟹放流量相对较小，管理部门缺乏详细的记载，因此相关数据无从获取。以2011 年放流量为基数向前逆算，假设后一年比前一年（即2010 年）的放流量增加10%，依次计算得到2001 年至2010 年浙江北部海域三疣梭子蟹放流量的估计值，计算得出的梭子蟹放流量的值可能会有些误差，但放流产生的补充量与野生相比数量很小，因此对结果影响不大（图2）。将估算得到的总补充量减去放流量产生的补充量，即为该研究最终计算使用的补充量。

1.1.2 海洋灾害数据

海面高度距平取自网站http：//www.cpc.ncep.noaa.gov；台风数据来自于http：//www.zs121.com.cn；赤潮面积数据来自于中国海洋年鉴。各因子的时间跨度均为2000-2014 年。赤潮指标选用每年浙江北部海域赤潮发生的面积；台风强度是每年发生在研究海域台风等级的总和；海面高度距平取平均值代表其指标强度。

1.2 研究方法

1.2.1 回归模型

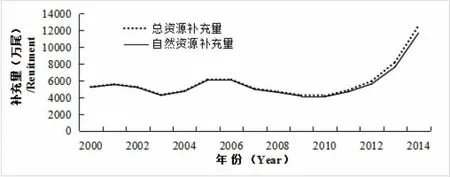
图2 浙江北部海域三疣梭子蟹总补充量与自然补充量Fig.2 The total recruitment and the natural recruitment of P.tuituberculators in the northern Zhejiang sea area

在建立预测模型的数据时，剔除了2002、2005、2007、2008、2010 和2012 的年度数据，这6 年的数据用于验证所建模型预测的准确度。剔除的数据包括所有年份数据前、中、后时间段，这样能够查看模型在不同时间段精度的变化，提高模型的可信度。

Matlab 在进行线性回归分析的过程中使用了遵循最小二乘法的数据拟合方式，该方式常见于曲线拟合中。由图2 可以看出，三疣梭子蟹补充量是曲线递增的。因此，此种回归分析方法适用于当前的拟合。

最小二乘法拟合的基本原理是对给定数据（xi，yi）（i=0，1，……，m）在取定的函数φ 中，求p（x）∈φ，使误差r=p（x）-yi（i=0，1，……，m）的距离平方和最小。即：

式中xi，yi为已知矩阵，p（x）为拟合函数或最小二乘解。在使用该方式前需要先求取有关数据之间关系的经验公式，即：推测得到的变量与结果之间的关系式。然后使用最小二乘法依次求取拟合函数与观测值之间的平方和直至结果最小。

Matlab 工具箱中提供了regress 函数，它可以实现变量与结果直接的多元线性回归，该函数调用格式如下：

函数中X 为自变量矩阵，此矩阵中包含了赤潮面积（AORT）、台风级数（TTWS）、海面高度距平（SSHA）的数据；Y 是由梭子蟹自然补充资源量组成的因变量矩阵；C 为拟合方程中各变量的回归系数，是个列向量；Bint 为回归系数估计值及其置信区间；R 和Rint 分别为残差向量及其置信区间；Stats 为用于检验回归模型的统计量，有4 个数值，判定系数R2，F 统计观测值，检验的P 的值，误差方差的估计。

Matlab 中最小二乘法非线性拟合所用到的拟合命令是nlinfit 函数。该函数在寻求最优非线性拟合参数时遵循了高斯-牛顿（Gauss-Newton）迭代规则，使用泰勒公式对非线性方程逐次进行迭代，确定最佳的回归模型（即：确定回归模型中各参数的回归系数）。该函数调用格式如下：

式中X 为自变量矩阵，此矩阵中包含了赤潮面积（AORT）、台风级数（TTWS）、海面高度距平（SSHA）的数据；Y 是由梭子蟹自然补充资源量组成的因变量矩阵；fun 是要拟合的非线性函数原型；beta0 为非线性函数原型各系数的猜测初始值；beta 为beta0 对应的计算值。在使用该函数对数据进行拟合时需要事先选择拟合模型的非线性函数原型。该研究中选择了三元二次方程作为数据回归分析的非线性函数原型。模型形式如下：

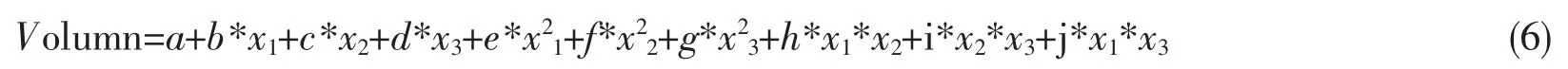
1.2.2 回归模型的检验

该研究中对Matlab 回归模型拟合结果的检验用到了5 项指标。第一项指标是梭子蟹补充资源量的相对误差（δ）；第二项指标是梭子蟹补充资源量与实际补充量的误差平方和（SSE）；第三项指标是梭子蟹补充资源量与实际补充量的方差（MSE）；第四项指标是梭子蟹补充资源量与实际补充量的标准差（RMSE）；第五项指标是梭子蟹补充资源量与实际补充量之间的确定系数（R2）。

在对回归模型进行检验的过程中，为了验证回归模型对未知年份的梭子蟹自然补充资源量预测误差。该研究使用剔除年份的梭子蟹自然补充资源量与预测值的相对误差进行了计算。比较（2002、2005、2007、2008、2010 和2012 年）梭子蟹补充资源量观测值与模型预测值的相对误差检验模型精度，表达式为：

式中，δ 为相对误差，x 为模型预测值，u 为梭子蟹自然补充资源量值。

误差平方和（SSE）是指将每个拟合数据与对应的实际数据相互做差，取平方，然后再求和得到的值。在对拟合数据和实际数据进行分析时SSE 的值越小表明，模型的选择和拟合效果越好，数据的预测结果也更为成功。SSE 的数学公式如下：

方差（MSE）的计算需要对求得的误差平方和（SSE）与参与拟合的数据个数相除。该值的大小也能够反映出模型的拟合效果，即MSE 值越小，模型的拟合效果越好。MSE 计算公式如下：

标准差（RMSE）是对方差的开方。与方差、误差平方和一样都是从拟合值与原始值的大小关系出发解释模型的拟合效果。RMSE 数学表达式如下：

与SSE、MSE、MSE 不同，确定系数（R2）表示了原始数据的平均值与模型各拟合值之间的关系。使用确定系数分析拟合效果时，其值越接近1 表示远程变量对原始值得解释性越强。

2 研究结果

2.1 显著性筛选结果

表（1）为使用GAM 对主要海洋灾害因子进行筛选，得到的与三疣梭子蟹补充量相关性达到显著水平（P＜0.05）的3 个因子。剔除掉不显著的因子包括风暴潮和厄尔尼诺等。

表1 显著影响浙江北部海域三疣梭子蟹补充量的海洋灾害因子筛选结果Tab.1 Screening results marine disaster factors that significantly impact the recruitment of P.trituberculatus in the northern Zhejiang sea area

2.2 三疣梭子蟹自然补充资源量线性回归模型结果

使用Matlab 中的regress 函数，对以上筛选出的3 个因子对梭子蟹补充资源量建立多元线性预测模型。构建的预测模型为：

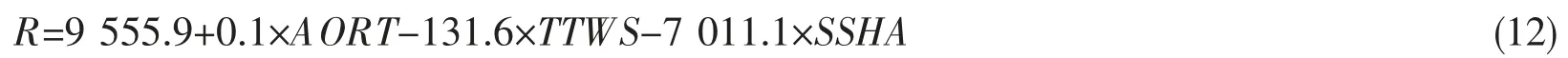
式中，R 为三疣梭子蟹自然补充资源量的预测值，AORT 为赤潮面积，TTWS 为台风级数，SSHA 为海面高度距平。三疣梭子蟹补充资源量线性预测模型拟合结果（表2）显示，均方根误差为1 403.5，确定系数为0.479.

将剔除随机年份的各海洋环境因子数据代入多元线性回归模型，便可得到预测值与梭子蟹自然补充资源量的对比结果。2002、2005、2008、2010、2012 年份梭子蟹自然补充资源量的预测值与估计值的相对误差分别为16.7%、15.9%、12.5%、41%、3.5%，平均误差值为17.92%（图3）。

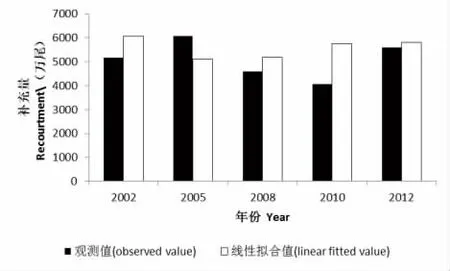
图3 浙江北部海域三疣梭子蟹补充资源量线性模型估计值及其观测值Fig.3 The observed value and the linear fitting value of recruitment of P.tuituberculators in northern Zhejiang sea area

表2 浙江北部海域三疣梭子蟹补充资源量线性预测模型拟合结果Tab.2 The fitting results of the linear prediction model for the P.tuituberculators in northern Zhejiang sea area

2.3 三疣梭子蟹自然补充资源量非线性回归模型结果

同样选择台风级数、赤潮面积、海面高度距平3 个因子作为影响三疣梭子蟹补充资源量的因子进行建模，使用matlab 的nlinfit 函数建立多元非线性预测模型：

式中补充资源量参数含义与式（12）一致。三疣梭子蟹补充资源量非线性预测模型拟合结果（表3）显示，均方根误差为680.4，确定系数为0.971 5.

将随机剔除年份的海洋环境因子数据代入多元非线性回归模型，得到预测值与梭子蟹自然补充资源量的对比结果。2002、2005、2008、2010、2012 年份梭子蟹自然补充资源量的预测值与估计值的相对误差分别为-9.8%、-23.7%、29.3%、10.7%、-7.5%，平均误差值为16.2%（图4）。

图4 浙江北部海域三疣梭子蟹自然补充量非线性模型估计值及其观测值Fig.4 The observed value and the nolinear fittedvalue of the recruitment of P.tuituberculators in the northern Zhejiang sea area

表3 浙江北部海域三疣梭子蟹自然补充资源量非线性预测模型拟合结果Tab.3 The fitting results of the nonlinear prediction model for the P.tuituberculators in northern Zhejiang sea area

3 讨论

从拟合结果可以看出，三疣梭子蟹自然补充资源量非线性预测模型要优于线性模型。三疣梭子蟹补充资源量线性回归模型、非线性回归模型之间是存在差异的，不同预测模型对梭子蟹补充资源量数据拟合是不同的，具体表现如下：

首先，线性回归模型基于现代统计学的理论，且应用广泛。其中模型的参数估计理论在建模过程中占据重要位置，因此得到统计学家的重视。他们既要研究模型参数估计理论及方法还需要利用结果对未来观察值进行预测。而在实际应用中，因被控对象的非线性、时变性和不确定性，因此非线性回归模型需要在掌握大量观察数据的基础上，利用数理统计方法建立因变量与自变量之间的回归关系函数表达式。

其次，不同类型的回归模型对三疣梭子蟹补充资源量预测模型的反映层面是不同的。该研究所用到的线性、非线性拟合模型分别是从不同层面描述了梭子蟹补充资源量的变化状况。其中三疣梭子蟹的线性回归模型的结构属性在分析中具有恒定性，即其输入变量与输出变量都满足叠加原理。因此在梭子蟹补充资源量与环境因子年际数据变化较小时，能很好地反映出梭子蟹补充资源量的变动与环境因子的关系；非线性拟回归模型在描述输入变量与输出变量不成正比，它描述的三疣梭子蟹自然自然补充量预测模型曲线具有动态性，非线性回归模型在描述梭子蟹补充资源量变动与年际动态变化更加精确，这与梁颖等（2015）在研究身体姿势控制的线性和非线性评价中的结论一致，其认为非线性模型分析下的自变量能够更加全面地解释因变量，能够得到有效的生理学参数，发现更多因变量层面的信息[28-29]。管纯凤等[30]对辽宁省渔业经济总产值的预测与研究中，利用多元线性回归模型对辽宁省渔业经济总产值预测。预测结果表明，多元线性回归模型的预测结果误差较大。

再次，不同类型的梭子蟹补充资源量预测模型对梭子蟹补充资源量的拟合可能具有显著性差异。在建立三疣梭子蟹补充资源量线性模型与非线性模型的基础上，该研究对这两个不同类型的回归模型进行了差异性比较，发现这两个方程之间都存在显著性差异（P＜0.05）。在线性拟合方程完整地描述三疣梭子蟹补充资源量的生长情况上某些方面是非线性拟合方程替代不了，比如，线性拟合方程对每一组变量的初值不敏感，而非线性拟合方程对初值较敏感，依赖性较大。这就证明了三疣梭子蟹补充资源量预测模型仅仅通过线性模型和非线性模型来描述梭子蟹补充资源量补充资源量的变动时可能存在偏差，是不完整的，不能完全反映出三疣梭子蟹补充资源量变动的实际情况。线性模型与非线性模型在拟合梭子蟹补充资源量的过程中都存在误差，片面性。因此，张日东利用神经网络来综合非线性系统的预测控制，降低了系统结构的复杂性、减轻了运算负担。同时它将非线性预测方程转化为一系列简单直观的线性预测方程并利用线性解析方法求取控制律。这种方法不仅整合了非线性模型和线性模型的优点，还降低了计算难度[31]。

最后，不同类型的梭子蟹补充资源量回归模型所描绘的梭子蟹补充资源量预测曲线的起始点可能存在一些差异。通过对三疣梭子蟹补充资源量线性模型估计值及其观测值和三疣梭子蟹自然补充量非线性模型估计值及观测值的比较中，可以发现线性拟合模型的起始点要明显高于实际三疣梭子蟹补充资源量的起始点，而非线性拟合模型的起始点与实际三疣梭子蟹补充资源量的起始点相重合。原因正是上面提到的非线性回归模型对初始值的依赖性较大。

该研究旨在探究更为准确的基于环境因子的三疣梭子蟹补充资源量预测模型，结果基本达到了三疣梭子蟹资源补充量预测要求。但是研究还存不足，需进一步完善：首先，该研究考虑灾害因子有限，渔业资源数量的变动是环境因子以及人类活动等多方面因素相互干扰的综合结果。其次，浙江省大规模增殖放流始于2001 年，而对梭子蟹增殖放流的详细记录始于2011 年，之前数据确实无法获得，采用模拟计算，在计算过程中，对估算得到的参数难免会产生一定的误差，最终计算出梭子蟹补充资源量只是一个粗略值，理想的补充资源量的计算还需根据营养关系、敌害关系、群落、生态结构等实际情况加以调整。因此，在今后的研究中，将选择不同区域，并搜集更多的捕捞、放流、气候、环境及灾害因子数据，综合多方面的因素来研究三疣梭子蟹补充资源量的变动，进一步完善三疣梭子蟹补充资源量的预测模型。