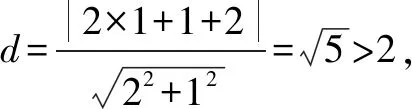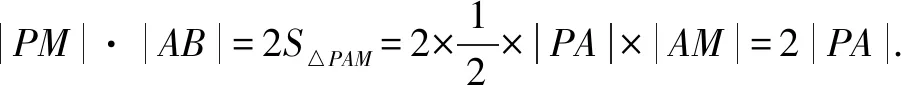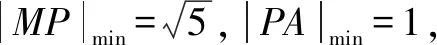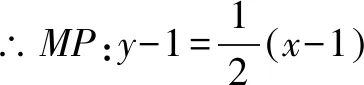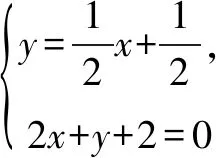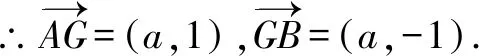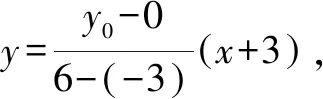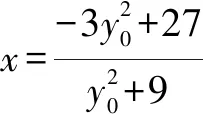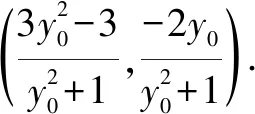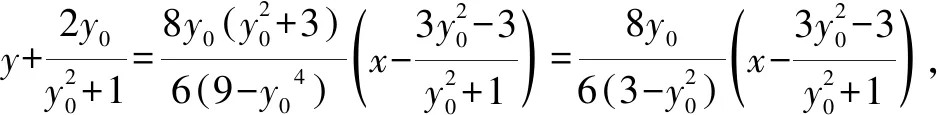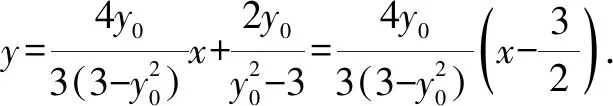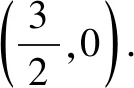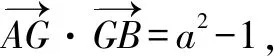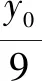以高考卷谈高三备考的几点建议
何正文
(广东省肇庆市百花中学 526020)
笔者参与2020年Ⅰ卷的数学评卷工作,对部分学生在一些题目上犯了一些可以避免的错误感到可惜,对部分学生在一些题目上由于没有养成良好数学思维而缺乏灵便方法感到惋惜,因此在对试卷进行分析和评阅后,笔者归类为核心概念,数据分析,空间想象,数学思维五个方面的原因.
一、 核心概念模糊
例1 (2020年全国Ⅰ卷理选择题第1题)若z=1+i,则|z2-2z|=( ).
解析由题意可得:z2=(1+i)2=2i,则z2-2z=2i-2(1+i)=-2.故|z2-2z|=|-2|=2.故选:D.
此题为试卷第一题,考点为考查复数的运算法则和复数的模的求解等知识,属于基础题.由题意首先求得z2-2z的值,然后计算其模即可,选错的学生大部分选择了C答案,错误地将复数的模与开方混为一谈,这是复数相关概念模糊的典型.
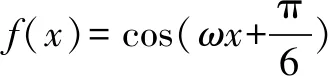
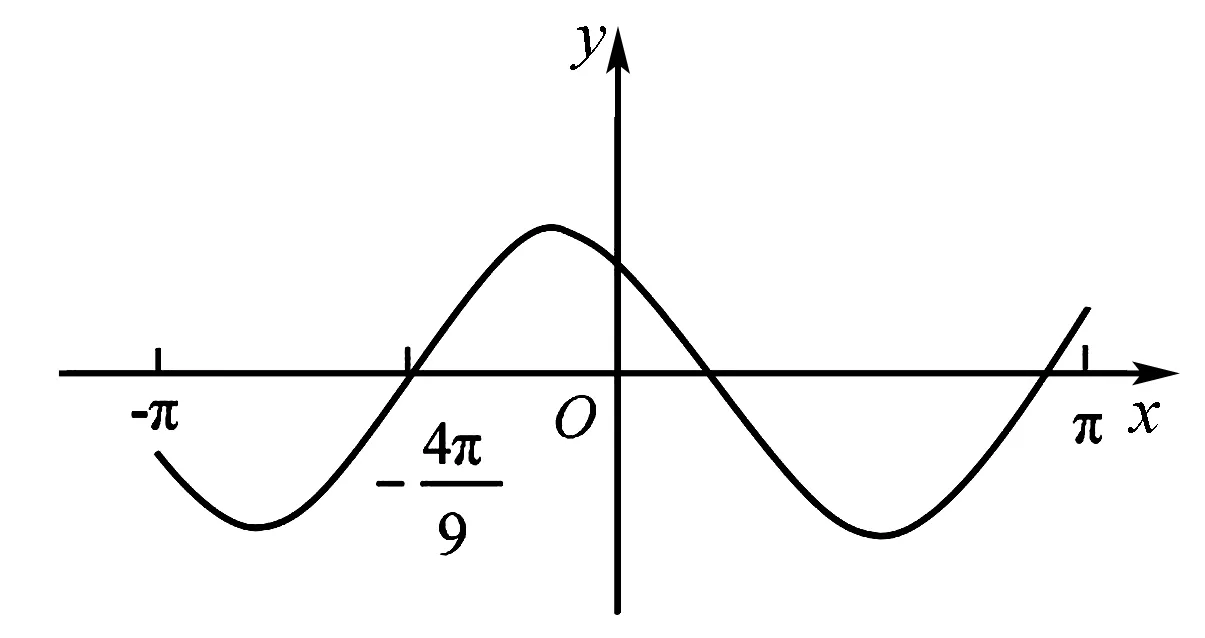
图1
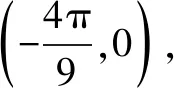
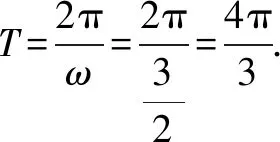
故选C.
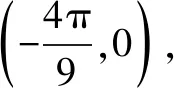
二、建模能力欠缺

图2
例3(2020年全国Ⅰ卷理选择题第3题)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
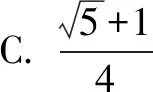

故选:C.
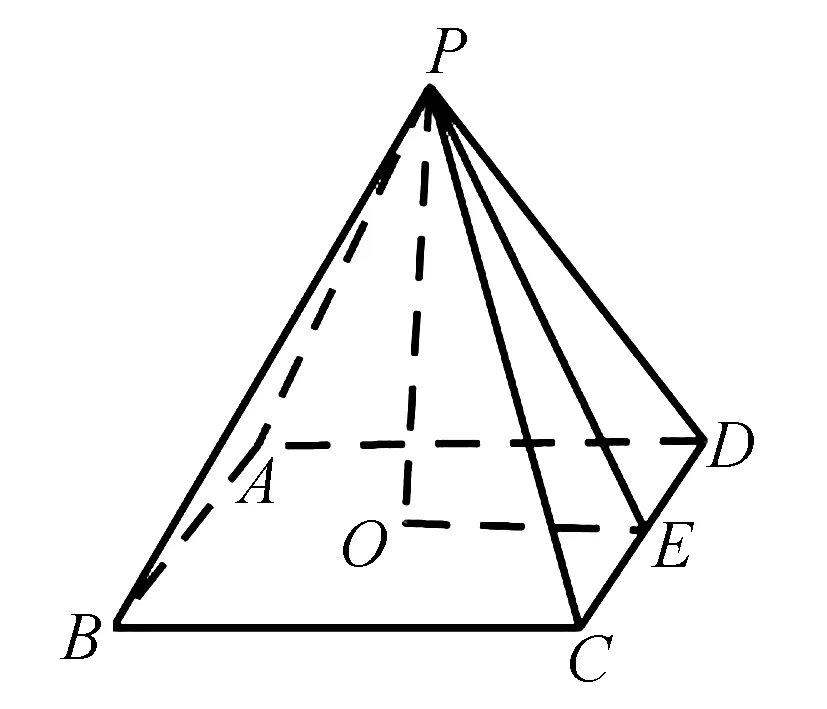
图3

例4(2020年全国Ⅰ卷理选择题第12题)若2a+log2a=4b+2log4b,则( ).
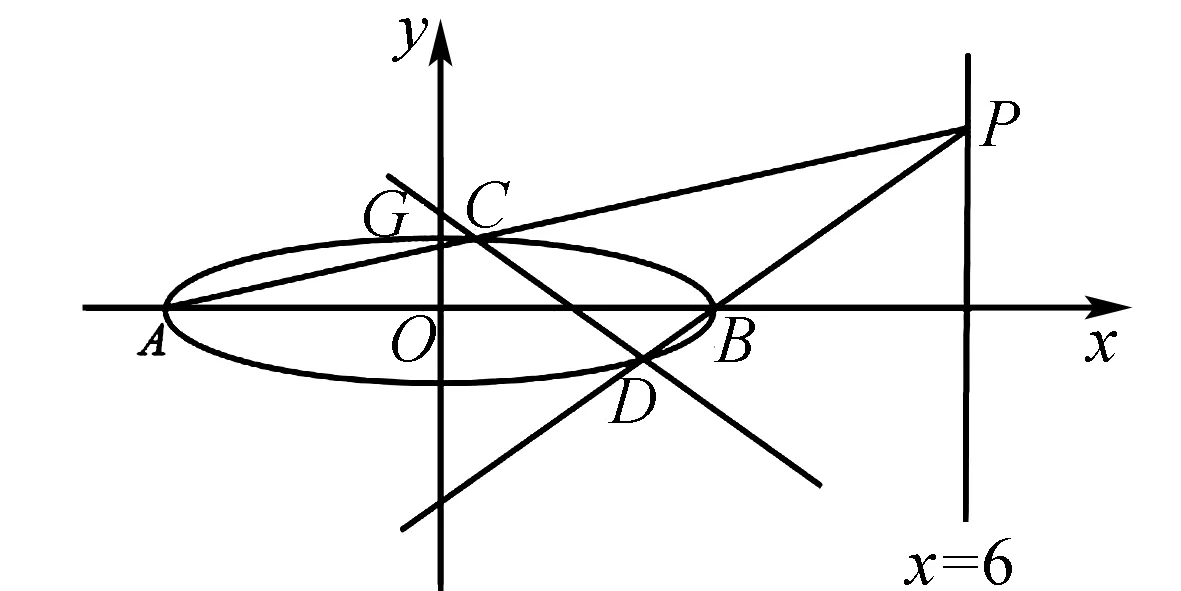
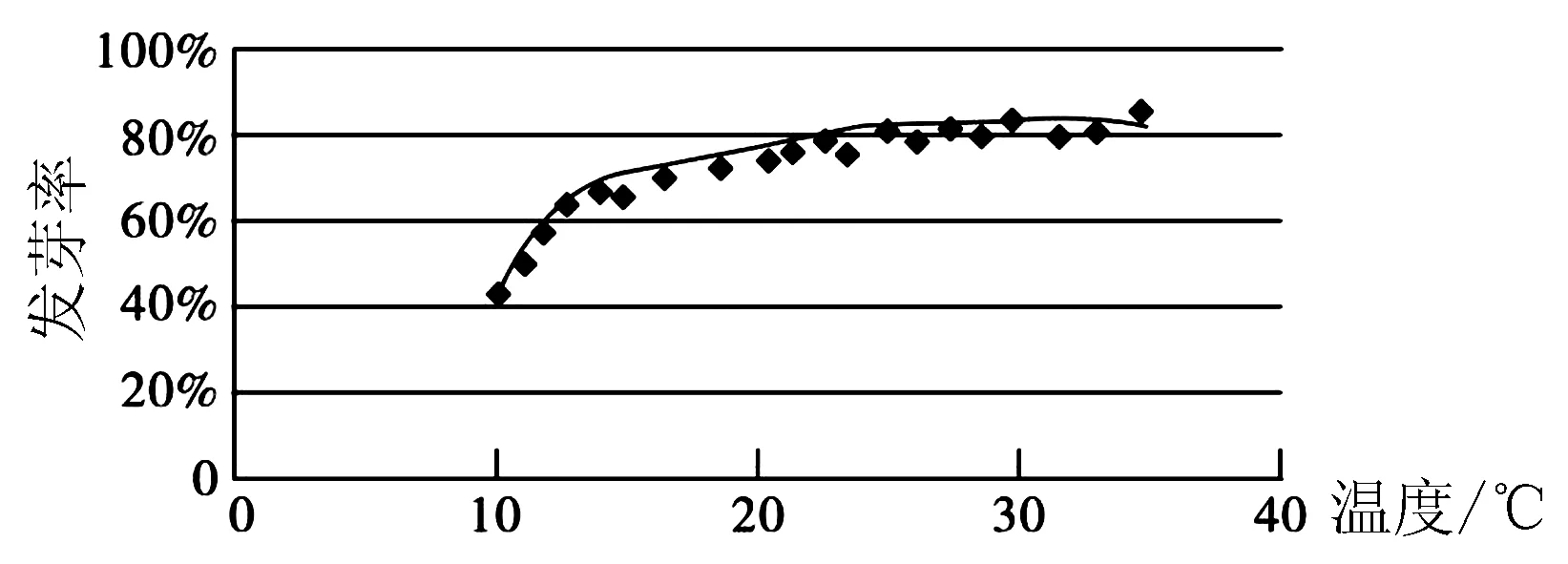
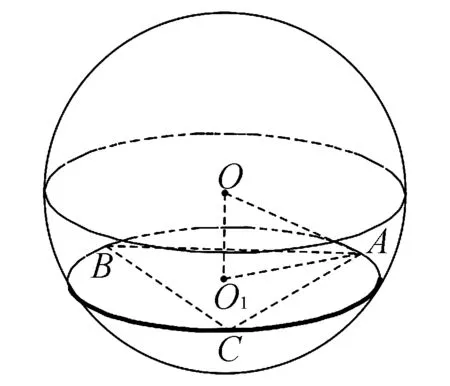
A.a>2bB.a<2bC.a>b2D.a 解析构建一条f(x)=2x+log2x函数模型,则f(x)为增函数,因为2a+log2a=4b+2log4b=22b+log2b, 所以f(a) f(a)-f(b2)=2a+log2a-(2b2+log2b2)=22b+log2b-(2b2+log2b2)=22b-2b2-log2b, 当b=1时,f(a)-f(b2)=2>0,此时f(a)>f(b2),有a>b2. 当b=2时,f(a)-f(b2)=-1<0,此时f(a) 故选:B. 此题为本题主要考查函数与方程的综合应用,涉及到构造函数,利用函数的单调性比较大小,是一道中档题.学生能不能构造f(x)=2x+log2x函数模型是解决这道题关键. 例5(2020年全国Ⅰ卷理选择题第5题)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图: 图4 由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( ). A.y=a+bxB.y=a+bx2 C.y=a+bexD.y=a+blnx 解析由散点图分布可知,散点图分布在一个对数函数的图象附近,因此,最适合作为发芽率y和温度x的回归方程类型的是y=a+blnx. 故选:D. 本题考查函数模型的选择,主要观察散点图的分布,应该属于基础题.考生却选不出正确答案,表面上这是一道根据散点图的分布可选择合适的函数模型.,其实更加是一道数据分析题,学生能从散点读出数据,与认识的函数图象对比数据分析,找出答案. (1)求甲连胜四场的概率; (2)求需要进行第五场比赛的概率; (3)求丙最终获胜的概率. 由对称性可知,乙赢的概率和甲赢的概率相等, 本题考查独立事件概率的计算,解答的关键就是列举出符合条件的基本事件,考查计算能力,属于中等题. (1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率; (2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率; (3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率. 学生往往看着今年的概率统计题目从字数比前两年少,但是数据分析却成为考察难点,18,19年概率统计字数多,但往往提供信息也多,而今年题目短,要分析的内容也多,缺乏数据分析能力的学生往往就无从下手. 例7(2020年全国Ⅰ卷理选择题第10题)已知A,B,C为球O的球面上的三个点,⊙O1为△ABC的外接圆,若⊙O1的面积为4π,AB=BC=AC=OO1,则球O的表面积为( ). A. 64π B. 48π C. 36π D. 32π 图4 根据圆截面性质OO1⊥平面ABC, ∴球O的表面积S=4πR2=64π. 故选:A 图1 本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.需要学生空间想象能力,由已知可得等边△ABC的外接圆半径,进而求出其边长,得出OO1的值,根据球截面性质,求出球的半径. ∴CF=CE=1, 本题考查利用余弦定理解三角形,考查计算能力,属于中等题.需要学生三维到二维的空间想象能力,在△ACE中,利用余弦定理可求得CE,可得出CF,利用勾股定理计算出BC、BD,可得出BF,这些都是从三棱锥空间中得到等量关系. 例9(2020年全国Ⅰ卷理选择题第11题)已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为( ). A. 2x-y-1=0 B. 2x+y-1=0 C. 2x-y+1=0 D. 2x+y+1=0 所以以MP为直径的圆的方程为(x-1)(x+1)+y(y-1)=0,即x2+y2-y-1=0,两圆的方程相减可得:2x+y+1=0,即为直线AB的方程. 故选:D 本题主要考查直线与圆,圆与圆的位置关系的应用,以及圆的几何性质的应用,意在考查学生的转化能力和数学运算能力,属于中档题.学生遇到一些P为l上的动点,感觉很迷茫,往往缺乏辩证分析数学思维,点到直线距离和半径比较推出直线与圆相离,挖掘出四点A,P,B,M共圆,且AB⊥MP,根据|PM|·|AB|=2S△PAM=2|PA|可知,当直线MP⊥l时,|PM|·|AB|最小,求出以MP为直径的圆的方程,根据圆系的知识即可求出直线AB的方程.步步为营,从条件引结果,从结果找条件.顺藤摸瓜的数学思维是解决这道题关键. (1)求E的方程; (2)证明:直线CD过定点. 解析(1)依据题意画出如下图形: 图1 ∴直线CD的方程为: 本题主要考查了椭圆的简单性质及方程思想,还考查了计算能力及转化思想、推理论证能力,属于难题. 从这次2020年全国Ⅰ卷理科数学卷试题,核心概念,数据分析,空间想象,数学思维五个方面作为着力点,帮助高三学生理清自身数学体系,要知己,还要知彼,在数学思维的高度理解题目,找到解题的突破口、解题规律,分析解题思路,平时教师鼓励学生谈他们自己的想法和困惑,加强对数据分析,空间想象方面的能力.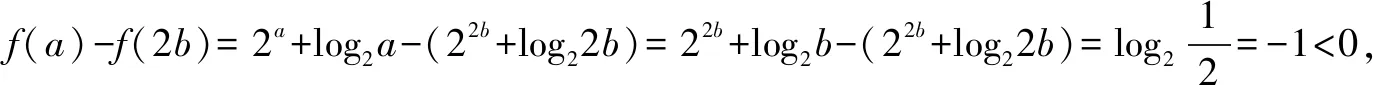
三、数据处理能力不足
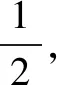

四、空间想象不足
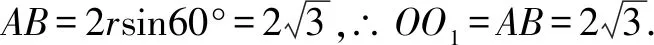

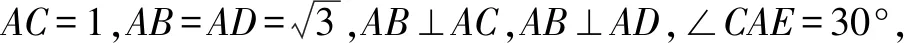


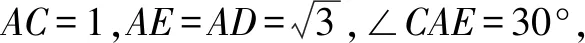
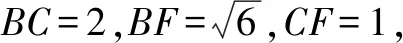
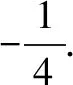
五、数学思维缺失