对一道经典竞赛题的商榷

邵 韬

(浙江省宁波市鄞州中学 315100)

一、对一道竞赛题的质疑

在高中物理磁场这一章，有这样一道竞赛题：

如图1所示，质量为m，带电量为q的正点电荷在水平面上运动，受到的阻力f=-kv.有一宽度为d的带状区域内存在方向垂直于水平面向里，大小为B的匀强磁场.问质点要穿过MN区域，初速度v0至少要多大，方向θ0如何？

当前的解析是由动力学方程出发，写出动量微分关系

在x方向上：-qvyB-kvx=max⟺-qΔyB-kΔx=mΔvx

在y方向上：qvxB-kvy=may⟺qΔxB-kΔy=mΔvy

考虑到刚好穿过MN区域时速度为零，对上式求和并代入始末条件

在x方向上： -qBd-kx=0-mv0cosθ0

在y方向上：qBx-kd=0-mv0sinθ0

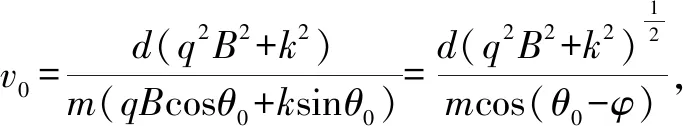
笔者认为解析中对穿出磁场时速度为零的假设存疑.恰好穿出磁场时速度的竖直分量为零，水平分量一定为零吗？

二、对粒子运动轨迹的研究

考虑到阻力始终与速度方向共线，洛伦兹力始终垂直于速度方向，建立自然坐标系.设t时刻粒子的速度为v，如图2.

角速度恒定，可设t时刻速度方向与x轴正方向的夹角为θ=ωt+θ0

粒子在xy方向上均做欠阻尼振动，速度不可能同时为零，仅在t→∞时，速度v→0，静止于某一点Q

由分部积分法可推导积分公式

得位移在直角坐标系中的分量

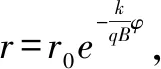
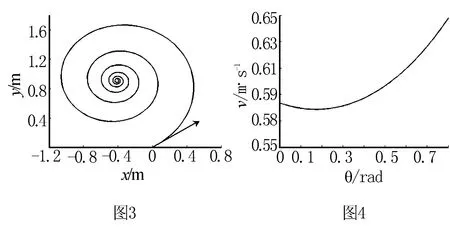
三、对习题的释疑

现在来解答本题，粒子刚好出磁场时vy=0，且第一次到达最高点，则ωt1+θ0=π

代入时刻t1，满足关系

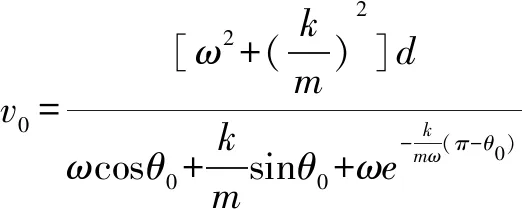
本式表明，粒子恰好能出磁场时，不同的入射方向θ0时所对于的初速度v0不同.仍然设定参数ω=1rad/s，k=0.1kg·s-1，m=1kg，并取d=1m，通过matlab软件绘制θ0-v0图，如图4.由图得当v0min=0.579m/s，此时θ0=0.180rad.题目的设计者本身是想考察物理学习者对临界思想在动量微分关系上应用技巧，但未考虑粒子运动的复杂性，因此本题只能从动力学方程入手求解.