解析数学建模在高中数学解题中的应用

曹彩霞

(江苏省海门市四甲中学 226100)

一、认真审题，构建函数模型

学生对函数模型并不陌生，在初中阶段已有所了解.高中数学涉及的函数模型更为深入，难度更大，授课中应注重该种模型的应用讲解.一方面，构建函数模型的关键在于找到自变量和因变量之间的关系；另一方面，为学生讲解常见函数模型解答方法.

例1有一片树林现有木材储蓄量为7100m3，要力争是木材储蓄量20年后翻两番，已达到28400m3.

(1)求平均每年木材储蓄量的增长率.

(2)如果平均每年增长率为8%，几年可以翻两番？

认真分析可知，解答该题目需要用到指数函数模型.对于(1)可设年增长率为x，根据题意可构建如下模型：7100(1+x)20=28400，即(1+x)20=4，由对数知识可知，20lg(1+x)=2lg2，即lg(1+x)≈0.0301，∴x+1≈1.072，所以x≈0.072=7.2%.(2)设y年可以翻两番，则构建模型为：7100(1+0.08)y=28400，解得y≈18.02，即十八年后可以翻两番.通过该题目的讲解使学生认识到，构建函数模型要认真审题，找到关键字构建对应数据模型.

二、把握特点，构建数列模型

数列模型是高中数学中较为常见的模型，包括等差数列和等比数列两种类型.应用该种模型解答数学问题时，判断是等比数列还是等差数列模型尤为关键.一方面，为学生总结等差数列和等比数列模型特点，使其认清两种模型之间的区别，结合题干找到首项、公差或公比.另一方面，解答数列模型时，应积极回顾所学的数列知识，包括前n项和、数列的单调性，尤其注意在求解等比数列前n项和时，应注重按照公比q=1和q≠1两种情况进行分类讨论.

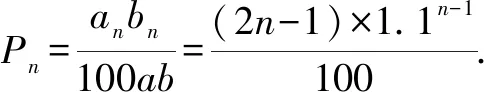
三、鼓励想象，构建空间模型

立体几何是高考的重要知识点，对学生空间想象能力要求较高.解答相关试题时构建合理的空间模型尤为重要.为使学生灵活应用空间模型解答立体几何试题，一方面，可运用多媒体技术，从不同角度向学生展示立体几何图形，加深其对立体几何点、线、面要素的认识，同时鼓励学生联想生活中的立体几何图形，合理想象，在头脑中形成清晰的空间对象.另一方面，要求学生具体问题具体分析，在求解的过程中，使用常规解法或向量解法，不断提高空间模型解答能力.

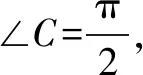
图1 图2

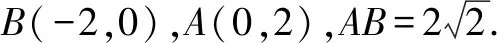
四、深思熟虑，构建概率模型

概率模型是高中数学的重要模型之一，相关试题难度并不大，但仍有一些学生在解题中出错，因此为提高学生的概率模型应用能力，一方面，为学生讲解常见概率模型，包括古典概型和几何概型，使其充分理解两种模型之间的区别，以及应用注意事项，如分析古典概型时，应注重当情况不确定时应注重分类讨论，保证考虑问题的全面性.另一方面，构建概率模型时，可围绕具体的问题情景，要求学生深思熟虑，认真分析，不断锻炼学生的模型分析以及构建能力.

例4某单位有3项业务要招标，共有5家公司前来投标，且每家公司对3项业务发出了投标申请，最终发现每项业务都有且只有一家公司中标.如果5家公司在各项业务中目标的概率均相等，问这3项业务由同一家公司中标的概率为多少？

综上所述，数学建模是一项重要的数学能力，根据题意构建正确的数学模型可明显提高解题效率，因此授课中应提高认识，结合高中数学所学的数学模型，为学生认真细致地讲解数学建模专业知识.同时创设相关的问题情景，对学生进行模型构建训练，积累数学建模经验与技巧，不断提高数学解题能力.