基于室内动静结合分割的射线跟踪加速方法

黄一航，江 虹，韩 宾

（西南科技大学信息工程学院，四川绵阳 621010）

（*通信作者电子邮箱491938847@qq.com）

0 引言

信息通信技术的快速发展，特别是5G时代带来了通信频率的提高、室内基站以及智能天线等技术的应用，使得对预测电磁波传播的精确性有了更高的要求。

射线跟踪（Ray Tracing，RT）算法是基于几何光学理论、几何绕射理论和电磁理论的确定性预测模型［1］，广泛应用于电磁传播仿真中。传统的射线跟踪算法在复杂的密闭三维环境模型下应用［2］能够提高算法精确性，但是成倍增加的无用求交次数会导致计算效率大幅度降低［3］。因此，业界一直在寻求如何大幅度降低无用交点的求解次数，以在保证射线跟踪算法精确性的同时能提高运算的效率。

1 射线跟踪算法工作机制

射线跟踪算法是通过模拟电磁波的传播路径，来确定多径信道在发射与接收机之间传播过程中所有可能存在的路径［4］。基本思想是将从源点辐射出的电磁波模拟为一条条射线，电磁在各自独立的射线管［5］内传播。依次沿着各条射线路径进行跟踪，判断射线是否碰到物体表面或者被接收点所接收。若射线遇到障碍物会发生反射、透射、绕射和散射现象，根据几何光学理论和一致性绕射原理［6］计算出各空间传播机制发生后的场强。跟踪射线直到场强衰减到预设阈值［7］，停止对本条射线跟踪。求得到达接收点的所有射线后，使用矢量叠加的方法计算出辐射源传递到目标位置的信号值。

在目标接收点处的总场强（单位：V/m）可表示为：

其中：接收点处矢量合并后的总辐射场强用Etotal表示；l为射线路径总条数；Ei为第i条射线路径末场的矢量场强。矢量场强Ei由式（2）［8］计算：

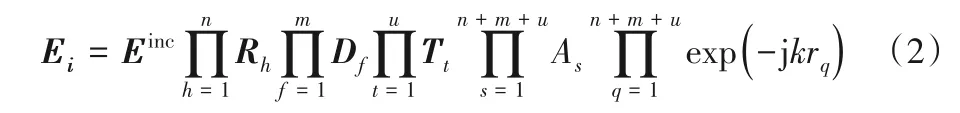
其中：Einc是射线在第一个反射、绕射或透射节点处的矢量辐射场；n为出现反射的总次数；Rh是在第h次反射时的并矢反射系数；m为出现绕射的总次数；Df是在第f次绕射时的并矢绕射系数；u为出现透射的总次数；Tt是在第t次透射时的并矢透射系数；As是经过反射透射或绕射后的扩散因子；rq是跟踪的射线的第q个传播节点到第q+1 个节点的距离，q为跟踪的信道总的空间传播机制节点数。

计算出终点场强Etotal后，接收点处的接收功率Pr可由式（3）［9］计算：

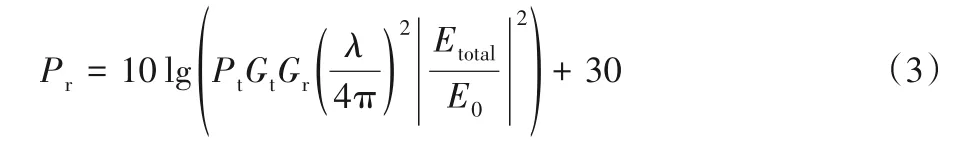
其中：Pt为发射天线辐射功率；Gt和Gr分别为发射天线和接收天线增益；λ为由电磁波频率计算出的发射天线工作波长；E0为发射点处初始电场强度。

由以上理论分析可知，影响射线跟踪算法预测精度和计算效率的因素主要有以下方面：

1）射线源发射的射线数量和射线之间的角度，决定了算法的预测精度。理论上发射间隔越小、跟踪的射线数量越多以及射线之间分布得越均匀，模拟电磁波传播的仿真算法就会越精确。本文使用相同大小正方形无缝覆盖单位球面的方式建立发射源［10］。

其中：（Vx，Vy，Vz）是需要跟踪的射线方向向量vt；Δθ是相邻射线间的角度，遍历n和m值即可得到所有射线的方向。因此间隔角度直接决定了射线源发射的射线数量。

因为跟踪一条完整的射线需要多次遍历所有的三维环境数据，所以当跟踪的射线数量越多，功率预测值虽然会更精确，但也将导致算法运行时长大幅增加。

2）空间内物体的数量与环境复杂程度决定了求交点运算次数的多寡。跟踪某一射线的基本步骤，是将该射线与检索范围内所有的物体表面进行求交点计算，找到交点坐标后再计算出相应的反射向量。因此跟踪的射线为了找到一个正确的碰撞点需要进行多次求交计算以预先找到多个交点坐标，而在这些交点中只有距起点Pstart最近的碰撞点是有效的碰撞点Pc和反射向量。即信号在传播过程中第一个碰撞到的障碍物交点是有效的，其余的求交点计算都是无用的运算。有效交点坐标Pc可以由式（5）计算得到：

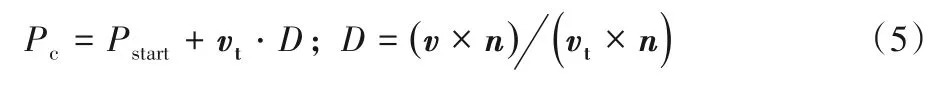
其中：D是根据相似三角原理计算得到的射线起点Pstart到交点之间的距离；v是射线起点与三维面内任意一点的向量；vt是跟踪射线的方向向量；n是三维面的法向量。

反射向量vRe由式（6）计算：

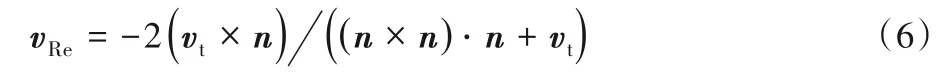
在整个射线跟踪算法运算中，只有能被接收点接收，且在射线传播路径中碰撞到正确三维表面的求交点计算才是有效计算，其余的交点计算都是无用运算。所以大量无用求交点运算导致了较低的计算效率。

在上述影响因素中，一般在达到精度要求后射线的间隔角大小是固定不变的，即发射源发射的射线数量通常不变。因此环境复杂程度（障碍物分布情况）主要决定了求交运算的次数。而随着环境复杂度的提高，无用求交运算次数所占的比例会大幅度增加。所以，减少算法中大量的无用求交运算是提高计算效率的主要途径。

2 基于三维空间分割的加速方法

在传统的射线跟踪算法中，正在跟踪的射线向量需要与环境模型内所有物体的三维表面进行求交点的运算［11］。随着环境复杂度的提高，绕射发生次数随之增加，使得算法需要跟踪更多的射线。并且环境复杂度和总射线数量的提高都会使得算法求交运算的次数大幅提升。

为此，文献［12］中提出了一种基于动态分区的射线跟踪加速方法。该方法根据环境模型内的障碍物分布情况动态划分区域，可减少射线与建筑物求交点次数；但是该方法只考虑了二维模型，不适合三维环境模型。因此，文献［13］中提出了使用正向发射与反向镜像混合的方法对原始射线跟踪算法进行改进；但该加速方法只是单纯改进了算法的计算方式，没有考虑到环境复杂度提高对算法计算效率的负增益。

因此，本文提出了基于静态空间分割与动态空间分割相结合的方法对三维环境模型进行空间分割，旨在大幅减少求交运算次数，有效提高算法的计算效率。

2.1 静态三维空间分割的加速方法

对三维环境模型进行静态空间分割，是将一个大区域平均划分为多个小分区以分摊区域中物体的数量，形成n级区域分割方式：一级分割将大区域平均划分为四部分；二级分割是将已经分割后的区域再次平均划分；后续的高级分割以此类推。射线跟踪每次只在射线当前所在分区Nold中检索碰撞点，若在该分区没有碰撞点，则射线离开当前分区Nold进入到下一个分区Nnew，并在Nnew内继续检索碰撞点，直到跟踪的射线到达接收位置或信号衰落权重超过预设阈值为止。如图1所示为空间分割方法流程。

对大区域进行空间分割后，检索碰撞点的算法将不需要和大区域内所有的物体表面进行求交点运算，只需在当前射线所在的小分区中进行碰撞检索，这样可以大幅度减少跟踪一条射线所需检索的碰撞点的次数。

因此，正确判断射线当前所在的分区，是静态空间分割方法的关键。如式（7）所示：

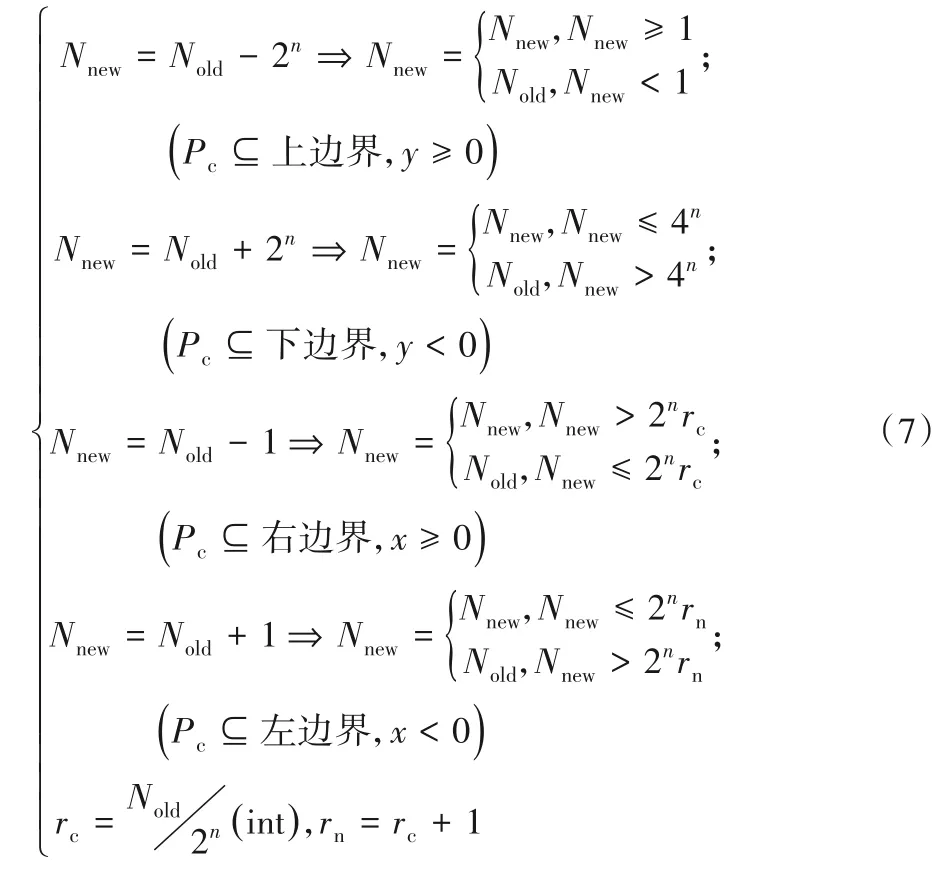
其中：Nold为射线当前所在的分区序号；Nnew为射线将要进入的分区序号；n为空间分割等级；Pc为射线碰撞点坐标；x和y是射线三维方向向量中的x值与y值。

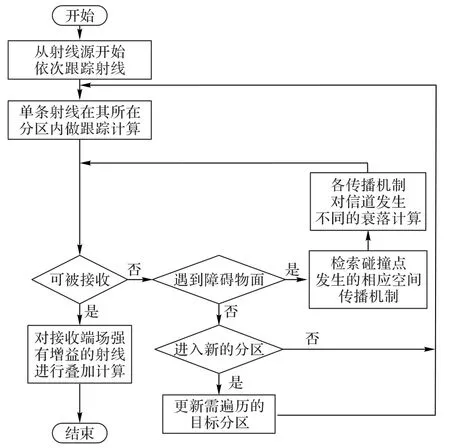
图1 空间分割方法流程Fig.1 Method flow of space segmentation algorithm

当射线的碰撞点Pc在分区的边界上时，可根据式（7）计算得出射线下一次范围检索的正确分区序号。

理论上对空间分割得越细，求交点运算计算量减少得越多，算法的效率也会越高。但是每细分一次区域不可避免会增加8 条分区的边界面，且一个三维物体通常为6 个表面，因此，当一个小分区中包含物体的表面数量少于等于6 条时就不能再细分区域。

图2（a）是没有进行空间分割加速的无线传播三维建模俯视图，使用的是原始射线跟踪算法对传播过程进行跟踪仿真。内部矩形部分是三维环境中各物体的三维模型俯视图，内部线条是跟踪算法跟踪到的能从信号发射端到接收端的无线三维信道模型，该模型可以作为后续对改进加速方法模型精确度的对比验证模型。图2（b）是静态一级空间分割的三维俯视效果图，使用一级射线跟踪加速方法对无线信道进行跟踪。在同一个三维环境模型下和图2（a）的原始跟踪算法作对比验证，可以看出两张俯视效果图中无线信道三维模型的数量和布局都一致，所以各级的静态加速方法没有降低算法的精确性。

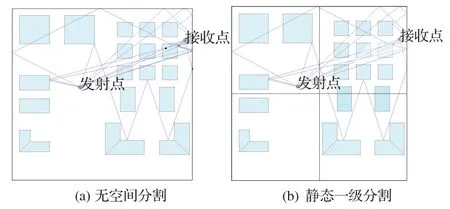
图2 环境空间分割俯视图Fig.2 Vertical views of environmental space division

2.2 动态结合静态的三维空间分割的加速方法

在三维环境下，虽然单独使用静态空间分割可以大幅提高计算效率。但在某些特殊情况下，静态分割方法提升算法效率的作用会失效。如图3 所示，当跟踪射线的相邻两个碰撞点间横跨了多个小分区时，由于算法会遍历横跨的各小分区中所有的物体面，所以无用求交运算的比例将逐渐接近传统的射线跟踪算法，使得在该情况下算法的计算效率并没有获得提高。

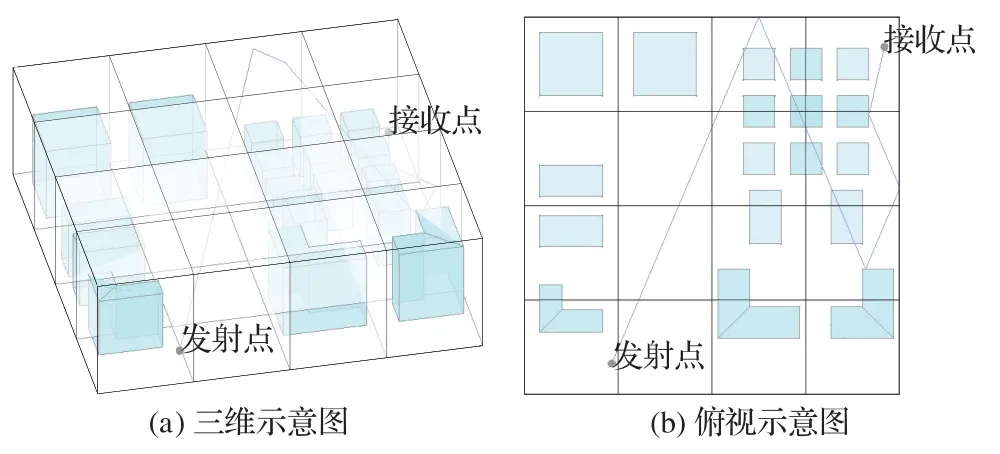
图3 射线一次性穿越多个小分区情况Fig.3 Ray traversing multiple small divisions at once

因为射线跟踪是在三维环境中进行，所以上述特殊情况发生的原因大概率是跟踪射线的该段传播高度过高，超越了其所在小分区物体的最高高度，不能在小分区内形成碰撞点。所以两个相邻碰撞点之间可能将跨越多个分区。

为了改善以上问题，本文在静态空间分割的基础上设计了一种基于高度划分的动静结合分割方法。实际密闭环境下的障碍物都会有一个最高高度，所以可以根据如下方式设计动静结合的空间分割，以进一步提高算法效率：

1）原始三维环境区域内所有物体高度的集合为h，则根据式（8）动态空间分割的阈值hd应是该区域内最高物体的高度值。

2）假设密闭空间高度为H，将整个三维环境模型根据分割阈值hd动态分割为上下两部分：上半部分空间合并划分为一整块空白区域；下半部分空间依旧使用静态空间分割的方式划分区域。

3）与静态空间分割类似，实现该方法需要正确识别跟踪的射线当前所在的分区序号。如式（9）所示：

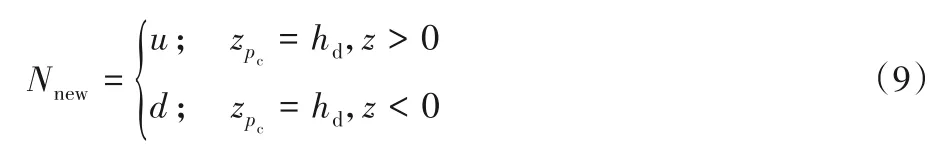
其中：Nnew为射线将要进入的分区序号；为射线碰撞点所在的高度；z为射线三维方向向量中高度值；u为上半部分分区序号；d为下半分区中某静态小分区序号，根据后续遍历法判断射线具体进入的小分区。

动静结合的分割方法可以最大限度地提高算法的计算效率。当只有静态空间分割时，跟踪某些角度的射线时，检索一个碰撞点可能一次会穿越多个小分区，如此造成的无用求交检索也会较多，导致计算效率大幅降低。因此本文使用对高度的动态分割方法结合静态的空间分割改进了算法的不足。如图4 所示，上升的射线进入动态分割的上半分区，只需检索一个上半分区便可替代原本静态方法需要检索的多个小分区，找到下一个碰撞点位置，大大减少了无用面与射线的求交运算次数。在图4 的三维环境模型下，此加速方法的算法效率在静态法已经提升的基础上还会有9.8%左右的提高。

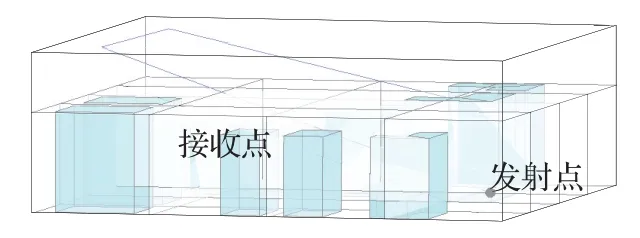
图4 静态与动态空间分割Fig.4 Static and dynamic space divisions

2.3 分区实现

本文的空间分割方法使用了四叉树的原理［14］。四叉树是一棵重力平衡树，通过对目标根节点空间进行平均四分，直至满足预测条件停止，最终形成一棵层次分明的树。空间分割步骤如下：

1）对真实环境建立模型后，获取环境模型的二维投影数据，通过坐标平移，使投影数据中最小位置点置于坐标原点，形成初始大区域。

2）检索环境模型中所有物体的高度确定最大值，该值作为动态分割的动态阈值。

3）对动态分割后的下半部分区域做静态空间分割。初始平均划分为2×2排列的4个子分区并排序（如图5所示），然后统计各分区中物体数量。

4）若子分区内的物体总数大于预设阈值，则该子分区返回步骤3）继续进行静态分割，直到所有分区内物体数量小于阈值。

5）动态与静态空间分割完成后，判断环境中每个物体分别所属的小分区序号，采用遍历法判断。

上述空间分割方法实现的重要一步，是确定空间内各物体所属小分区，一旦出现位置误判，最终计算所得的仿真结果将会和真实数据相去甚远。本文使用遍历法来精确判断物体所在的小分区：物体棱边的平面线段与分割边界做交点计算判断交点所在分区，若无交点则判断线段在分割边界的哪一侧，进而确定物体所在小分区。

以图5 所示的一级静态分割为例，使用式（10）判断物体的棱边线段所属的小分区，进而判断物体所在的分区序号。N为线段所在的分区序号，X为指向坐标x轴正方向的分割边界单位向量，Y为指向坐标y轴正方向的分割边界单位向量，L为两分割线交点指向棱边线段上任意一点的方向向量。

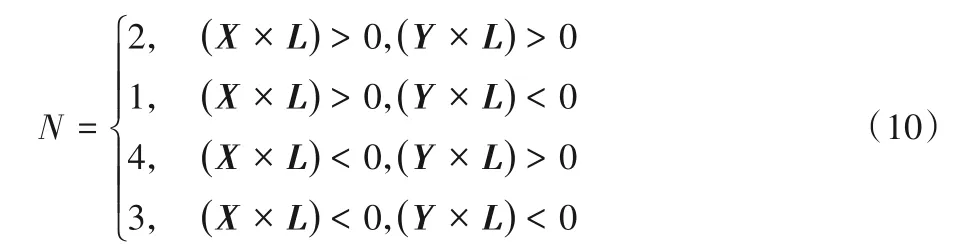
更高级分区的相关判断以及式（9）中d序号的确立沿用上述公式的衍生公式。

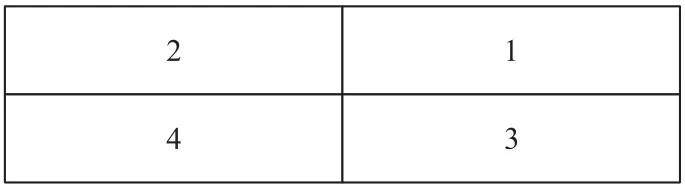
图5 静态空间分割排序示意图Fig.5 Schematic diagram of sorting for static space division

2.4 方法分析

2.4.1 时间复杂度

根据上述加速方法实现流程，分析得到加速方法跟踪一条射线的计算时长T由以下几个部分构成：1）时间T1，根据大环境中物体的分布情况动态分割区域，且将各物体的表面分配到各自所在小分区中的耗时；2）时间T2，信道射线跟踪过程中与物体表面进行的求交点运算以及进一步计算射线入射、出射向量性质的耗时；3）时间T3，跟踪的射线穿越边界时判断进入的下个分区的耗时；4）时间T4，判断跟踪的射线是否能被接收区域接收的耗时；5）时间T5，计算接收区域信道传播特性的耗时。则可知：

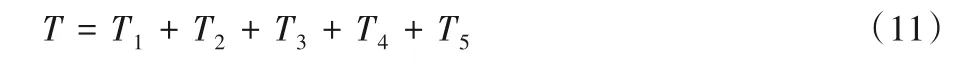
然而，由于需要跟踪的射线数量庞大，加速方法是一个多层循环运算，且T1和T5只需一次计算即可得到结果，所以T1和T5在时间复杂度中所占的比例极小，可以忽略不计。

假设大环境中总的物体表面个数为n、动态分割出了g个小分区，即可知各个小分区中平均拥有的物体表面个数为n/g。因为T2中主要的运算是射线遍历所在小分区中所有物体表面进行求交点等相关计算，若跟踪一条射线与一个物体表面做相关计算耗时为k1，那么分区中一次求交点计算的耗时为(n/g) ×k1。假设检索到一个射线碰撞点平均需要遍历v个小分区，且一条射线从开始到停止跟踪平均需要检索m个碰撞点，则时间T2为：

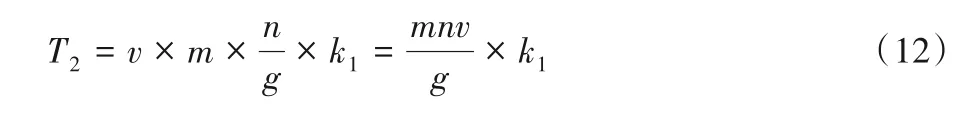
T3中的主要运算是当射线与分区中物体都没有交点时，根据射线方向向量一次判断进入的下一个分区。假设相关的操作耗时为k2，则时间T3为：

T4中的主要运算是每次检索到碰撞点后，判断射线是否能被接收区域所接收。假设相关的操作耗时为k3，则时间T4为：

相对于T3和T4，T2的耗时占了绝大部分时间，这首先是因为求交点等相关运算的计算过程复杂，而其他耗时部分的主要运算过程相对比较简单，因此使得k1远大于k2和k3；其次，则因为T2同时与大环境中总的物体表面个数n、发生一次空间传播机制平均需要遍历的分区个数v以及重复检索空间传播机制的次数m都相关，且物体表面个数n不与T3和T4相关，且其数值远大于v和m的值。因此，可以忽略T3和T4，则加速方法的时间复杂度T可表示为：

2.4.2 空间复杂度

从加速方法的实现流程可知，加速方法的空间复杂度可以类似于时间复杂度，运算时的内存占用绝大部分是跟踪的射线与分区中的物体表面进行的求交点计算，且循环多个分区。因此，整个加速方法的空间复杂度S可表示为：

3 仿真与结果分析

3.1 验证改进算法精确度

首先验证改进算法相对于原始算法结果的精确性。改进算法可应用在任意三维空间环境模型，且复杂度越高改进算法提升效率比越高。对如图6 所示的AB路径进行功率预测值的对比仿真，各射线跟踪算法运行时原始数据都相同。本次验证的环境模型为12 m×12 m×4 m 的立方体结构，内部有18 个障碍物模型：9 个高度为2 m 的障碍物模型与9 个高度为2.5 m 的障碍物模型，共有105个需要遍历的物体表面。射线发射源发射频率60 MHz，发射源与接收点均为全向天线［15］，发射源间隔角为1.8°可向四周不同方向均匀发射2 万条射线，物体墙面介电常数为4.5［16］。起点A坐标为（-5.5，3，1），止点B坐标为（3.5，-3，1），总长约为10.8 m。在该路径上有55 个预测仿真点，间隔为0.2 m。仿真使用Intel i7 处理器，8 GB内存，Matlab仿真平台。

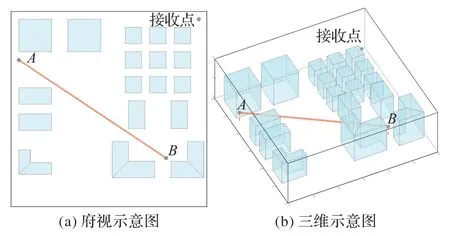
图6 用于验证算法改进前后功率预测值的仿真路径Fig.6 Simulation path for verifying power prediction values before and after algorithm improvement

图6所示AB路径上55个射线发射点，分别使用原始的射线跟踪算法和改进算法之间做预测对比分析。从图7 两种算法的功率折线图可以看出，原始跟踪算法与改进跟踪算法的折线图几乎重合。在同一个三维环境模型下，跟踪路径AB上各发射点发射出的模拟射线，使用改进算法的预测折线与使用原算法的预测折线差距非常小，仅在仿真位置39 位置处改进后的算法功率比原始算法高了0.03 dBm，偏差很小，误差在合理范围内，可视为精确仿真。

由图7 的折线图可以验证，改进后的跟踪算法几乎没有降低原始算法的预测精确度。

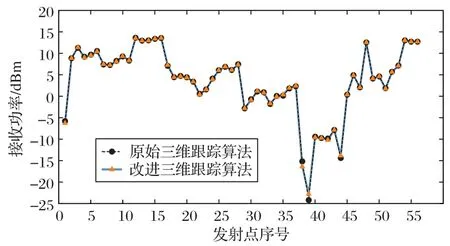
图7 在路径AB上使用原算法和改进算法的功率预测值对比Fig.7 Comparison of power prediction values using original algorithm and improved algorithm on path AB

3.2 验证改进算法高效性

在同一个三维环境模型下验证射线跟踪加速方法的高效性。选取图8 中的A、B、C三个位置点作为发射基站位置，依次使用无空间分割的原始算法、静态多级分割方法以及动静结合分割的改进方法运行仿真。

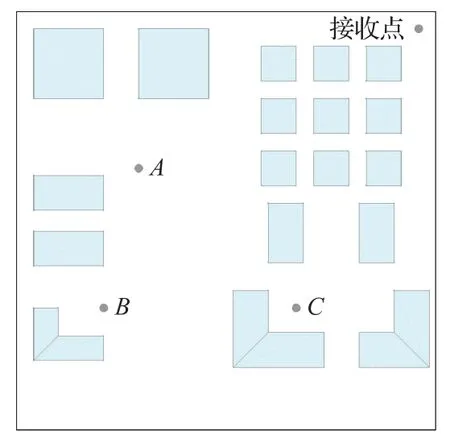
图8 改进算法高效性验证的基站天线分布Fig.8 Distribution diagram of base station antennas for improved algorithm efficiency verification

在验证对比中除了各空间分割方法不同以外，其余的所有初始数据、方法都相同。多次运行记录不同跟踪算法的总运行时间与总求交次数的数据，结果如表1所示。

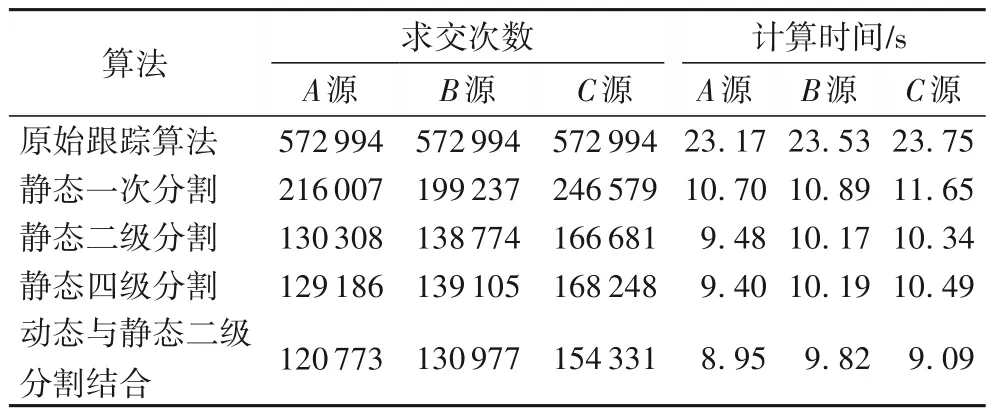
表1 高效性对比验证结果Tab.1 Efficiency comparison and verification results

因为射线跟踪算法以及本文的加速方法都是电磁仿真中的确定性仿真模型，所以多次重复运行同一个加速方法，总求交次数固定不变，而总运算时间会因为电脑CPU 占用等一些客观因素的影响发生波动。因此需要对总运算时间做多次仿真，计算均值。图9 为多次运行原始算法与本文的加速方法对图8 环境模型中A基站做信道仿真的总运算时间波动折线图。

根据图9 所示的时间折线图计算可知，使用原始算法多次重复仿真后其算法运算时间均值时间为23.172 2 s、标准差为0.056 4 s；使用本文的加速方法的运算时间均值为8.953 8 s、标准差为0.055 5 s。对于不同射线跟踪加速方法的标准差相差很小，因此客观因素对仿真时长的影响程度都相同，后续验证可使用多次仿真的时间均值来表示各射线跟踪方法运算的总时间。

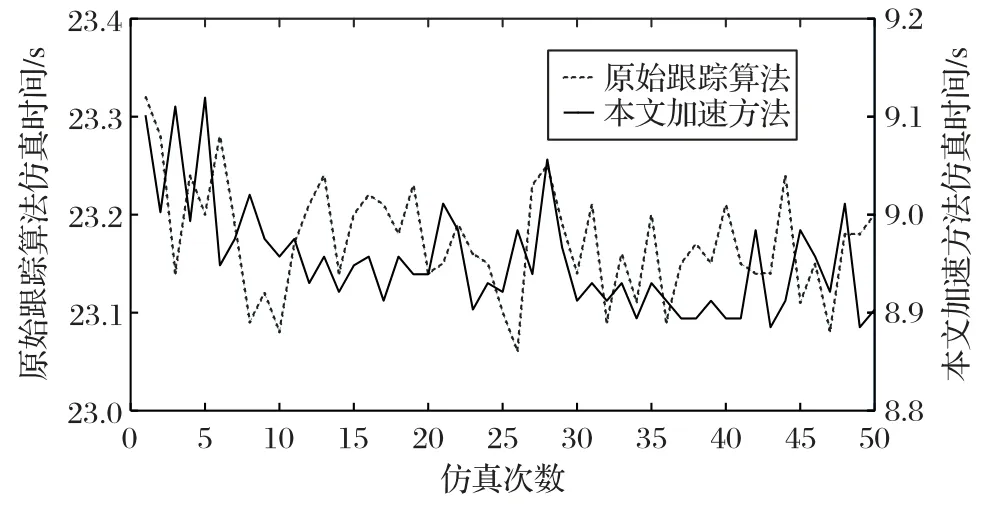
图9 仿真时间波动图Fig.9 Fluctuation graph of simulation time

比较分析得出以下结论：

1）动态与静态结合的空间分割加速效果最优，静态空间分割次之，传统的射线跟踪算法计算效率最差。

2）无分割的传统射线跟踪算法因为需要跟踪的射线数量确定，且每次对碰撞点的检索都是检索全区域，所以在该情况下A、B、C三个基站点的求交次数相同。但由于三个基站所处的位置不同，所以经过的路径不会相同，算法运行的总时间会有一定差异。

3）静态空间分割若没有依照环境密集度情况合理划分，比如分割等级分的过高，算法的加速效果将变得不明显，且反而有可能增加运算时间。而恰当的静态分割加速方法对比传统算法，在当前环境模型下的计算效率可以有61.4%以上的提高。

4）使用静态与动态空间分割相结合的加速方法对比只使用静态空间分割的算法，在当前环境模型下的计算效率在已经提升的基础上还会有9.8%左右的提高。

当然，在减少算法计算时间的同时也需要保证计算的精度。对本文的三维射线跟踪加速方法，因为射线与物体的相交点并不会发生改变，所以算法的精确度不会受到影响。

3.3 实验分析

使用本文中动态结合静态空间分割的射线跟踪加速方法与文献［12］中提出的改进算法作性能对比分析，都使用图8所示的三维环境模型以及A、B、C三个坐标源点作为发射基站位置，且其余仿真参数都相同。对比结果如表2所示。

表2 本文的射线跟踪加速方法与文献［12］算法对比Tab.2 Comparison between the proposed ray tracing acceleration method and algorithm in literature［12］

根据上述结论比较分析后可知，本文使用的加速方法相对于文献［12］算法在提升射线跟踪算法运算效率方面有更好的加速指标，进一步减少了使用射线跟踪算法对无线信道传播仿真的时间。因此，本文的加速方法是一种更快速的仿真算法。

仿真验证其他的如图10 所示简单三维环境模型，依次使用原始算法、静态分割方法以及动静结合分割的方法运行仿真，各完整运行50次后得到的平均运算时间数据如表3所示。根据动静结合加速方法的空间分割规则，该模型只能做基本的一次分割，不能再继续深入划分。

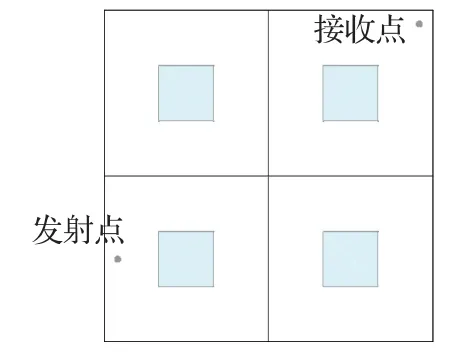
图10 简单三维环境模型Fig.10 Simple 3D environment model

表3 最小加速效果验证结果Tab.3 Verification results of minimum acceleration effect

从表3可得出以下结论：

1）动态与静态结合的空间分割加速效果最优，静态空间分割次之，传统的射线跟踪算法计算效率最差。

2）使用静态空间分割的射线跟踪加速方法对比原始算法计算效率提高了50.2%；而使用静态与动态空间分割结合的加速方法对比只使用静态空间分割的方法，计算效率在已经提高的基础上还能提升8.9%。

3）和3.2 节中表1 的结论数据对比分析可以验证，三维环境越复杂动静结合的加速算法提升计算效率的比例也会越高。

上述结果表明本文所提出的改进算法不仅可以大幅度地提高原始算法的计算效率，而且几乎没有降低算法的预测精度。验证了改进算法的高效性，也很好地改善了射线跟踪算法模型中预测精度与计算效率之间的矛盾。

4 结语

本文使用射线跟踪算法对空间环境中无线信号的传播进行信道仿真与三维建模，并且分析了原始射线跟踪算法在仿真计算过程中将产生大量的无用求交运算，导致计算效率过低的问题。因此，本文根据原始算法的不足之处，提出了一种提高计算效率的射线跟踪加速方法。该方法结合了动态空间分割与静态空间分割的方法，减少了跟踪计算过程中的无用求交点次数，提高了射线跟踪算法计算效率，降低了算法仿真运算时间。这能为电磁环境的实时仿真计算提供解决方法，是一种实用的射线跟踪加速方法。

然而，本文设计的射线跟踪改进加速方法有局限性，仅考虑了从减少求交次数的方面来减少仿真的运行时长。后续可以尝试，在保证算法精确性的前提下动态减少射线发射端需要跟踪的射线管数量，以达到加速射线跟踪仿真计算的目的。