基于缺陷比例限制的背景差分钢轨表面缺陷检测方法

曹义亲，刘龙标

（华东交通大学软件学院，南昌 330013）

（*通信作者电子邮箱569144312@qq.com）

0 引言

随着国内外铁路行业的蓬勃发展，列车的运行速度、运营里程、载重量都在日益增长，潜在铁路基础设施中的安全隐患也在日益凸显［1］。钢轨作为铁路轨道重要一部分，由于受持续行车、载荷及自然因素的作用，它的表面不可避免会产生各种磨蚀缺陷，容易危及行车质量与安全［2］。因此，及时发现轨面缺陷对保障铁路运输安全至关重要［3-4］。

目前，存在许多钢轨探伤方法，如超声检测、涡流检测、漏磁检测等物理方法［5-6］，但大多只能检测钢轨内部，且检测速度慢，检测结果对探测器工作状态敏感、不稳定［7］。相较于其他方法，基于机器视觉的检测方法因具有非接触、高速、低成本等优点被诸多学者研究。如Trinh 等［8］提出了一种实时的自动视觉轨道检测系统；该方法检测准确率较高，但只能对锚杆等轨道元件进行检测，扩展性较差。Dubey等［9］提出了最大稳定极值域的视觉检测技术用于轨道缺陷的检测，并且对缺陷的几何特征进行标记和可视化；但由于实际轨面缺陷形状各异，在有复杂噪声干扰时，精度有待提高。Min 等［10］提出一种基于机器视觉的形态学处理和方向链码的方法对缺陷进行快速提取，但该系统处在初步实现阶段，检测的实时性和对轨面光照影响的鲁棒性较差。深度学习是机器视觉的一个分支，源于人工神经网络，可以模仿人类思维模式记录和开发，深受学者青睐［11］。Zhang 等［12］提出了一种基于卷积神经网络（Convolutional Neural Network，CNN）和声发射（Acoustic Emission，AE）事件概率分析的轨道健康检测方法，检测结果较好；但由于要获取每个缺陷类别中缺陷样本的概率值均值，并将该值与判定阈值进行比较，耗时较多，实时性难以保证。Shang 等［13］提出基于CNN 的图像识别和分类的轨面缺陷检测方法。该方法有一定的检测效果，但在不同训练集中参数调整不易，有时召回率缓慢增加时，准确率迅速下降，结果并不稳定。基于深度学习的检测仍面临算法性能优化与改进、精度提升、模型轻量化等关键技术的挑战［14］，加之现实铁路线路繁多且所处区段各异、自然环境复杂多变，诸多方法在这些严苛因素干扰下的有效性难以保证。轨道图像会因光照不均匀、可识别的特征有限、对比度低、反射特性易变等特性，使得基于机器视觉的轨道缺陷检测仍存在诸多待研究的问题。

袁小翠等［15］提出了基于目标方差加权的类间方差阈值分割法WOV（Weighted Object Variance），直接对钢轨表面缺陷进行提取，对灰度分布不均的轨面图像有一定的检测效果；但实际线路中轨面缺陷较小，缺陷和背景大小有很大差异，会直接影响类间方差走势。该法虽对最大类间方差法Otsu［16］有所改进，但其本质还是试图最大化类间方差，因此对实际轨面图像检测的精度还有待于提高。为提高精度，Yu等［17］提出了一种从粗到细的缺陷识别模型，该模型从子图像级、区域级和像素级三个不同的尺度来对缺陷进行检测，能有效对抗光照反射不均的影响和其他噪声的干扰，但是同时考虑三个尺度具有一定的复杂性。为提高效率，贺振东等［18］提出基于背景差分的钢轨表面缺陷检测方法BGD（BackGround Difference），将视频中的背景差分法应用到单张的轨面图像中，有效减弱了光照、反射不均等影响，对块状缺陷检测效果较好，背景仅使用灰度列均值建立，虽然简单快速，但对阴影、锈迹等抗干扰能力较弱，且对线状缺陷的检测效果较差。闵永智等［19］提出基于图像灰度梯度特征的背景差分轨面缺陷检测方法BGD2（BGD based on gray gradient），该法基于双边滤波设计了一个平滑滤波器对背景进行建模，能够较好地检测裂纹和疤痕缺陷，但该方法参数过多，同一组参数无法适应形状大小各异的轨面缺陷，如逐一适配成本过高。

为此，本文提出了一种基于缺陷比例限制的背景差分钢轨表面缺陷检测方法。该方法主要包括轨面图像预处理、背景建模与差分、缺陷比例上限阈值截断、缺陷比例最大熵阈值分割、连通区域标记滤波五个步骤。首先采用基于双边网格的快速双边去噪方法对轨面进行去噪处理；其次利用轨面图像列灰度均值和列灰度中值快速建立背景模型，将预处理的轨面图像与背景图像进行差分，初步凸显缺陷；然后利用轨面图像缺陷占比较低的特征，对差分结果进行缺陷比例上限阈值截断，缩小差分图像背景灰度值范围，增强对比度，从而进一步凸显缺陷；随后再利用轨面图像缺陷占比较低的特征改进最大熵阈值分割，采用自适应加权因子对目标熵进行全局可变加权，选择最优阈值对截断结果进行分割，在保留缺陷必要信息的同时，减弱诸如锈迹、污渍、尘土等噪声干扰；最后利用连通区域标记法把缺陷面积低于钢轨损伤标准的区域判定为噪声，从而实现钢轨表面缺陷检测。

1 钢轨表面图像特征分析

由于铁路线路建造在不同区段上，列车运行在不同的自然条件下，并且车轮与轨面有不同接触状况，从而会导致同一轨面图像特征存在很大差异。如图1 所示，从左到右至少有强光照、正常、阴影、缺陷、锈迹和尘土等轨面区域。

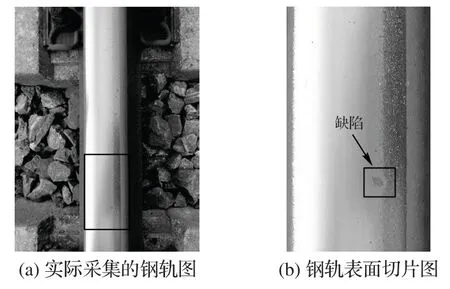
图1 实际采集的钢轨图像Fig.1 Rail image collected in practical environment

1.1 灰度值分布分析

由于轨面图像可识别特征有限，图像的灰度信息显得尤为重要。图2（a）所示为图1（b）的灰度分析划分图，沿列车行驶方向划有6 道纵线（C1～C6）：分别依次穿过强光照、正常、阴影、缺陷、锈迹和尘土轨面区域。垂直于列车行驶方向划有两道横线（R1、R2）：R1除未穿过缺陷区域外，和R2一样从左到右依次穿过上述6种不同轨面区域。图2（b）、（c）是纵横线段处轨面相对应的灰度变化。

分析图2（b）、（c）中的灰度分布曲线可以得出以下3 个结论：

1）全局范围内背景灰度值变化较大，局部范围内灰度变化较小。由于轨面的光照和反射特性不同，若从全局考虑，钢轨图像的背景往往具有较大的动态灰度范围（几乎从最大值到最小值）；若从局部考虑（沿着列车行驶方向的一条纵线上）光照和反射特性比较稳定；因此，局部窗口内往往具有较小的灰度变化。

2）缺陷与背景之间的灰度值无序。一般情况下缺陷的灰度值小于背景的灰度值，然而，由于光照和反射特性的不规则变化，这个顺序往往可以改变。如图2（b）中的一些带锈迹或尘土的像素与带缺陷像素相比，具有更小或相等的灰度值。

3）局部范围内包含缺陷的轨面区域灰度值有明显突变。如图2（b）的345～365 行、图2（c）的175～200 列的灰度值较低且变化较大。

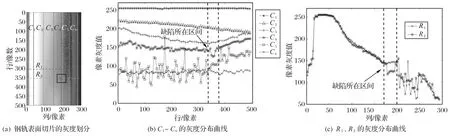
图2 钢轨表面图像灰度分布Fig.2 Grayscale distribution of rail image

1.2 列灰度均值、中值规律分析

由1.1 节可知，沿着列车行驶方向的一条纵线上光照和反射特性比较稳定，灰度值变化较小，因此列灰度信息价值较高。贺振东等［18］643提出了基于列灰度均值的背景差分方法对缺陷进行分割，Gan 等［20］提出了基于均值漂移方法的粗提取器在轨面中沿纵向建立背景模式对缺陷进行粗定位。均值是通过整组数据计算得来的，容易受数据中极端值的影响（如轨面图像某条纵线上存在缺陷或其他噪声时），所以仅基于列灰度均值建立的背景模型并不稳定；中值则是通过数据排序得来的，不受极端值影响，但它并不能代表整体集中趋势。所以本文将均值和中值综合考虑以探寻轨面列灰度值的规律。

从本实验室收集整理的钢轨图像数据库中随机选取200张带缺陷的轨面图像，记录每一张图像缺陷的列坐标范围；随后计算图像缺陷范围内每一列的灰度均值（grayscale MEAn of Column，CMEA）和灰度中值（grayscale MEDian of Column，CMED），并比较该范围内每一列CMED 和CMEA 的大小关系（注：设置一个flag标记，仅当某一列的CMED 大于CMEA 时，标记flag=1），随后统计每张图像缺陷范围内flag=1 的个数，当该值超过其缺陷范围列数的90%时，判定该张轨面图像缺陷范围内的CMED 大于CMEA（记为A 类轨面）；同法可判定CMED 小于CMEA（记为B 类轨面）。最后画出A、B 两类轨面图像的CMEA、CMED分布曲线图，分析其潜在规律。

本次实验样本中76%属于A 类轨面，24%属于B 类轨面，通过观察可知：A 类轨面往往背景较均匀，B 类轨面的钢轨图像往往背景较为复杂，有大量的噪声干扰。分析轨面图像的列灰度均值、中值的分布曲线可知：无论是A 类轨面还是B 类轨面，缺陷范围以内的列不是CMEA 大就是CMED 大，并且有明显的突变和差异；缺陷范围以外的列，CMEA 和CMED 几乎相等，差异很小，如图3所示。

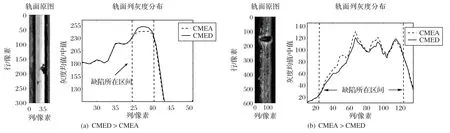
图3 钢轨表面图像的列灰度均值、中值分布曲线Fig.3 Distribution curves of column grayscale mean and median of rail surface image

1.3 缺陷比例分析

从钢轨图像数据库中随机选取165 张带缺陷的轨面图像，为了降低人工成本，图像中所有的缺陷都被标记为最小外接矩形，因此缺陷面积近似于其最小外接矩形面积；最后计算轨面图像的缺陷比例。

通过如图4 所示的统计直方图可知，有约95%的轨面图像缺陷区域占轨面总区域的比例不超过10%，存在极少数缺陷占比较大的，但也均不超过30%。因此实际铁路轨道中绝大部分的轨面是无缺陷的，即使存在缺陷，缺陷占轨面总区域的比例也很小。

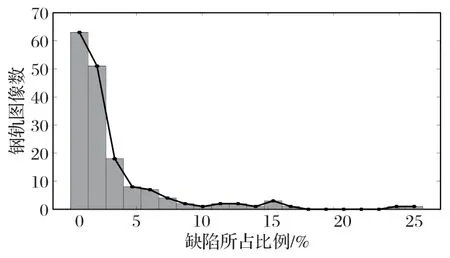
图4 钢轨表面缺陷占比统计Fig.4 Statistical chart of rail surface defect proportion

2 本文方法

2.1 轨面缺陷检测方法流程

图5 为本文轨面缺陷检测方法的流程，主要包括三个部分：轨面图像的预处理、基于缺陷比例限制改进的背景差分对比度增强（BGD based on Defect Proportion Limitation，DPL_BGD）和基于缺陷比例限制改进的最大熵阈值分割（Maximum Entropy based on Defect Proportion Limitation，DPL_ME）。其中预处理部分采用基于双边网格的快速双边去噪［21］；DPL_BGD 部分包括列均值和列中值快速背景建模与差分、缺陷比例上限阈值截断；DPL_ME 部分包括缺陷比例最大熵阈值分割、连通区域标记滤波。

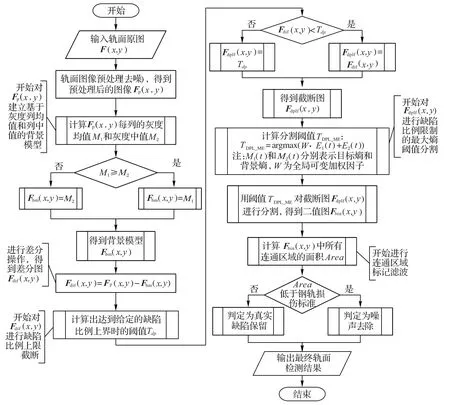
图5 轨面缺陷检测方法流程Fig.5 Rail surface defect detection method flowchart

2.2 改进的背景差分对比度增强（DPL_BGD）

2.2.1 基于列灰度均值、中值的背景建模

由于单张钢轨图像的缺陷检测无法从安装在测试列车下的摄像机生成的视频序列中学习到背景模型，因此动态目标检测中的背景差分方式不能直接用于轨面缺陷检测［22-23］。为此，贺振东等［18］643提出了基于列灰度均值的背景建模方法。

假设垂直列车行驶方向为x轴，沿着列车行驶方向为y轴。计算出每列的灰度均值，建立钢轨背景图像模型：

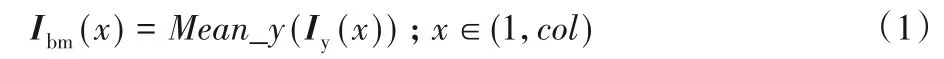
其中：Ibm(x)为第x列的轨面背景；Mean_y(·)为计算每列灰度均值的函数；Iy(x)为第x列上所有像素的灰度值；col为轨面图像列数。

基于列灰度均值建模容易受极端值影响使背景模型不稳定，而使用复杂的方法建立背景模型又会牺牲时间效率（如基于双边滤波设计的滤波器建模［19］223，耗时较大，参数过多）。考虑到轨面图像缺陷范围外CMEA 和CMED 差异很小，背景建模时在缺陷范围外取其任意一值均可，而缺陷范围内的CMEA 和CMED 之间有明显的突变和差异，且缺陷处的灰度值往往比较低，所以在缺陷范围内取其较大值能在差分时使背景图像与原轨面图像缺陷之间尽可能产生更大的灰度差值，以更好地凸显缺陷，使差分结果具有更高的对比度。

为此，本文提出基于列灰度均值、中值的背景建模方法，计算出每列的灰度均值和中值，取其较大者建立背景模型：

其中：Fbm(x)为第x列的轨面背景；Mean_y(·)为计算轨面每列灰度均值的函数；Median_y(·)为计算轨面每列灰度中值的函数；M1和M2分别为轨面每列的均值和中值，M1=Mean_y(Fy(x))，M2=Median_y(Fy(x))；Fy(x)为第x列上所有像素的灰度值；col为轨面图像列数。

2.2.2 背景差分

为了更好地突显缺陷，减少光照、反射不均等干扰，将预处理后的图像与背景模型进行差分操作，得到差分图像：

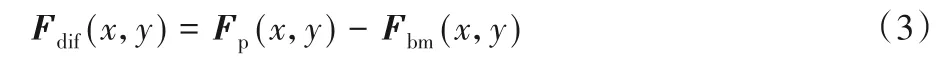
其中：Fp(x，y)为预处理后的图像；Fbm(x，y)为背景模型。

如表1 所示，本文差分方法在耗时较少的情况下，较文献［18-19］的差分结果具有更高的对比度。

此外，通过图6 的差分前后灰度分布对比图可知，差分后增强了缺陷目标从复杂的背景中分割出来的可能性（注：图6（a）、（b）左侧的C1～C5五条划分线分别穿过缺陷1、阴影、正常、缺陷2 和锈迹轨面区域）。如图6（a）所示，不同的轨面区域具有不同的灰度值，且灰度值的跨度范围较广，找不到一个合适阈值能将缺陷目标从复杂的背景分割中分割出来。

如图6（b）左侧所示，经本文方法差分后的差分图像，极大减弱了光照及反射不均带来的干扰，且背景均匀，较好地凸显了缺陷区域，这将有利于轨面缺陷检测；如图6（b）右侧所示，不管何种轨面区域都具有相近的灰度值，所以此时较容易将缺陷目标从复杂的背景中分割出来，但还有不少背景可能会在分割时被错分为缺陷。因此，本文将设计一个缺陷比例限制滤波器来对差分图进行缺陷比例上限截断，进一步增强差分图的对比度，使背景被错分为缺陷的概率降低。

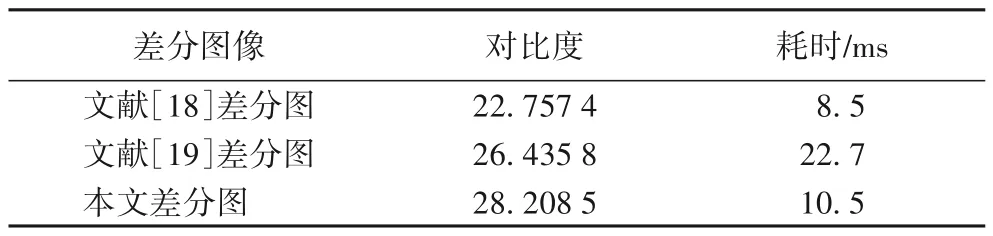
表1 文献［18］、文献［19］和本文差分图的对比度和耗时对比Tab.1 Contrast and time consuming comparison between different image methods in reference 18 and 19 with proposed method

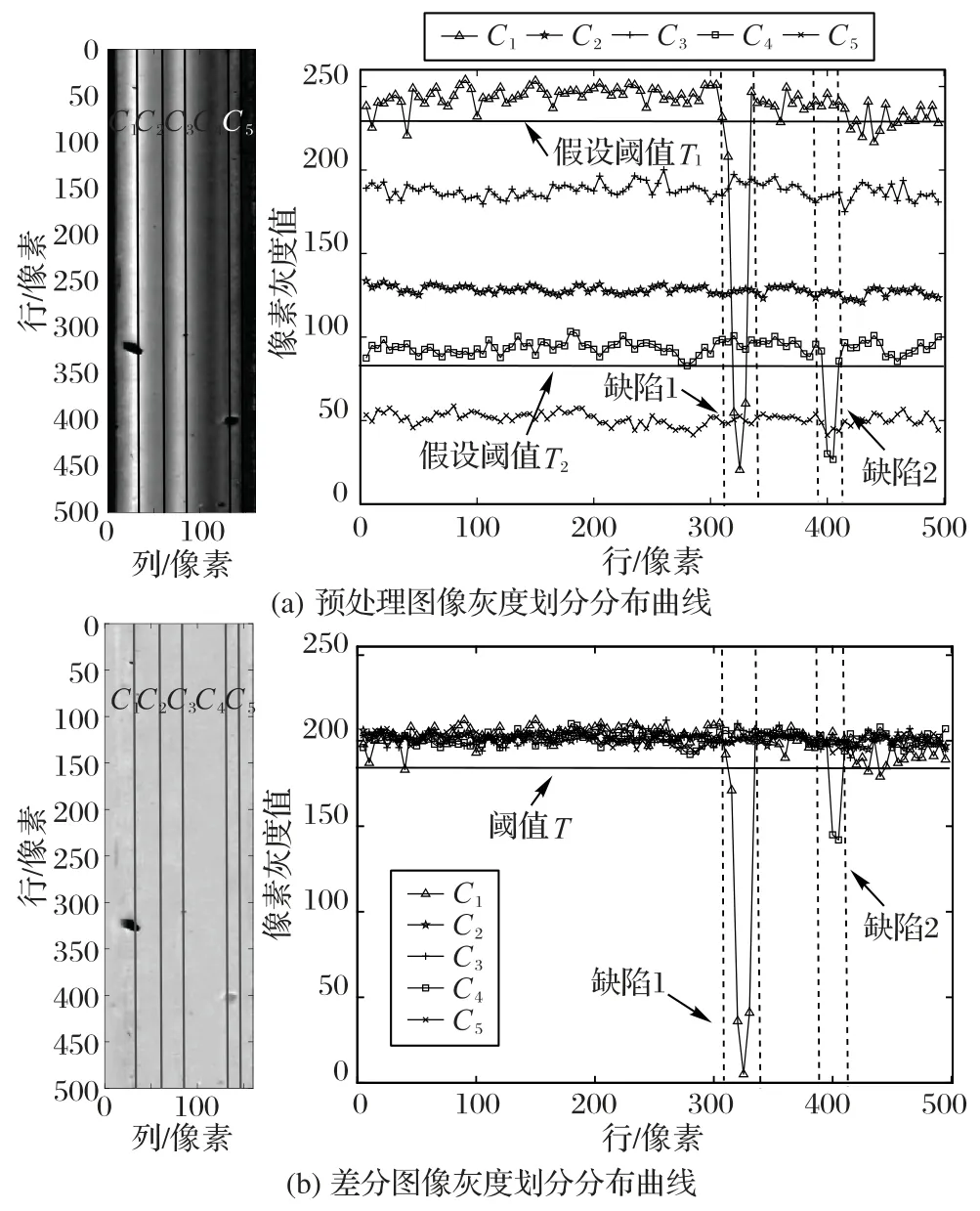
图6 差分前后灰度分布曲线对比Fig.6 Comparison of grayscale distribution curves before and after difference

2.2.3 缺陷比例限制滤波

基于以下两个事实，差分图像Fdif(x，y)可以进一步地增强：第一，差分图像中缺陷处的灰度值小于背景的灰度值；第二，轨面绝大部分无缺陷，即使存在缺陷，缺陷占轨面总区域的比例也很小，极少数缺陷比例较大的，也不超过30%。因此，本文通过缺陷比例限制滤波器进一步增强差分图像，该滤波器需要给定一个缺陷比例（defect proportion，dp）的上界，然后根据具体轨面图像给出一个阈值Tdp对其差分图进行缺陷比例上限阈值截断。

考虑到一个L个灰度级的差分图（L是图中出现过的灰度级总数），令N为差分图中像素的总数，ni（i=0，1，…，L）是具有灰度级为i的像素数量，假设已经选定一个阈值t，C1是灰度级为［0，t］的一组像素，C2是灰度级［t+1，L-1］的一组像素。N1(t)是集合C1中直到灰度级t的累计像素个数，表示为：

则截断阈值Tdp由如下公式定义：

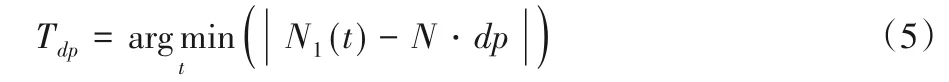
阈值Tdp可将差分图Fdif(x，y)像素分为两组CO=Fdif(x，y)＜Tdp和CB=Fdif(x，y)≥Tdp，CO包括缺陷和背景，CB只包括背景。因此通过缺陷比例限制滤波器处理后的截断图像Fdplf(x，y)可以表示为：

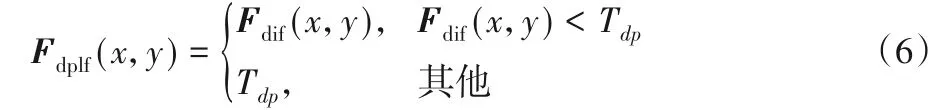
如图7 所示，经过缺陷比例上限阈值截断后，减小了差分图背景的灰度值范围，在保留缺陷必要信息的同时具有更均匀的背景，更强的对比度（注：经计算，差分图的平均背景方差和对比度分别为24.15 和28.21，截断图的分别为16.42 和42.83）。

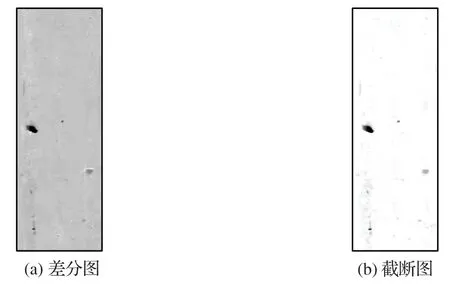
图7 差分图和截断图对比Fig.7 Comparison of difference image and truncation image

综上所述，经过基于列均值、中值的背景差分和缺陷比例上限阈值截断后，能极大提升轨面图像的对比度，这将极有利于后续步骤中的轨面缺陷分割。

2.3 改进的最大熵阈值分割（DPL_ME）

2.3.1 最大熵阈值分割方法

Kapur等［24］提出最大熵阈值（Maximum Entropy，ME）分割法，此法把图像分为目标和背景两部分，熵代表信息量，熵越大代表图像信息越大，ME就是找出一个最佳阈值使得目标和背景两部分的熵之和最大。

现假设某图像具有k个灰度级，其对应灰度级k发生的概率为Pk，已经选定一个阈值t，C1是灰度级范围为［0，t］的一组像素，C2是灰度级范围为［t+1，L-1］的一组像素。

C1和C2分别表示目标和背景，则它们各自的熵E1（t）和E2（t）可以分别表示为：

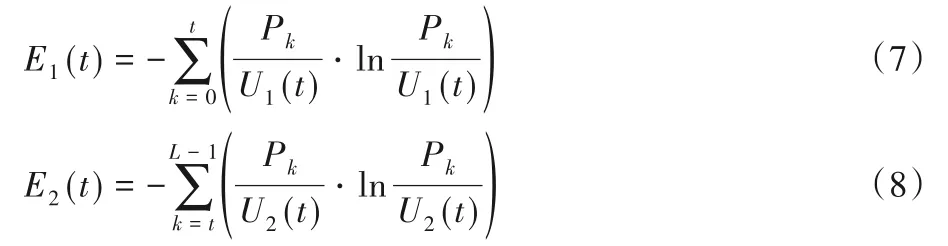
其中：U1（t）和U2（t）分别为目标集合C1和背景集合C2发生的累计概率。

因此，ME法最优的阈值t被确定为：

ME 为钢轨图像阈值分割提供了一个很有吸引力的解决方案，但它并不完美，因为还存在较多的噪声，如图8（c）所示。因此，本文将提出一个新方法来改进ME 使得分割后的图像具有更高的质量、更少的噪声。

图8 ME方法的截断图分割结果Fig.8 Truncated image segmented by ME method

2.3.2 基于缺陷比例的ME阈值分割方法

如图9（a）所示，截断图特征较为特殊，其全局灰度分布为最右侧呈左向半单峰，即绝大部分背景灰度值都在255 附近；如图9（b）所示，灰度累计概率曲线图，U（255）常常大于0.5，而U（i）～U（220）常常小于0.01（其中U(·)表示到达某灰度级时的累计概率），这一事实影响了最大熵函数阈值的选取。

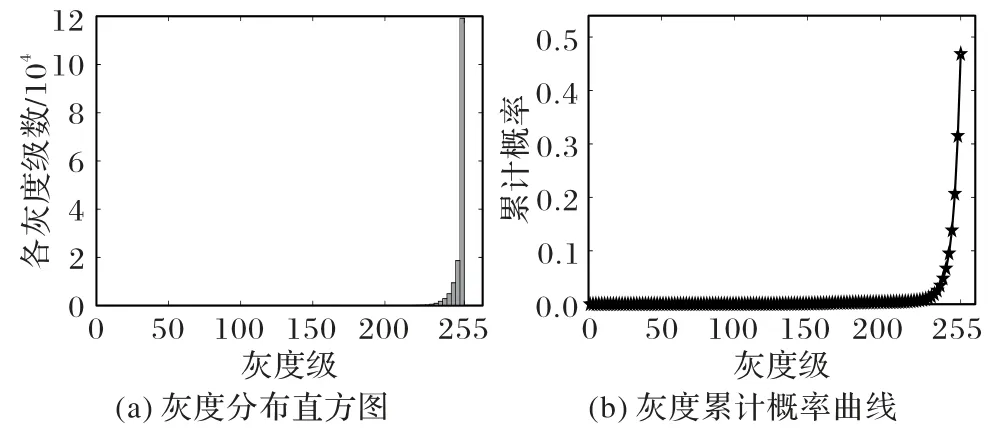
图9 截断图灰度分布和累计概率分析Fig.9 Grayscale distribution and cumulative probability analysis diagram of truncated image

最大熵的阈值TME主要由目标熵E1（t）决定。理想的分割阈值应使目标熵相对较小，背景熵相对较大，这样才能得到更小阈值，消除更多的噪声。为了达到这个目标，本文将对最大熵方法中的目标熵进行全局可变加权，使得加权后的目标熵小于或等于原始目标熵，因此，DPL_ME 阈值分割法可表示为：

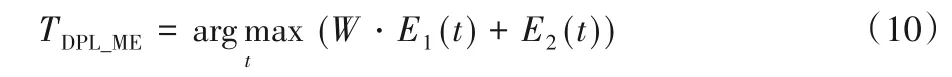
其中：E1（t）和E2（t）分别表示目标熵和背景熵；W为全局可变加权因子，W取值应为［0，1］，从而使W·E1(t) ≤E1(t)成立。当图像中缺陷目标较大时，W应取较小值；当缺陷目标较小时，W应取较大值；对没有缺陷的轨面图像，加权因子W应该趋近于1。由于不同轨面上缺陷的形状大小不一，若采用全局恒定不变的加权因子，恐不适用实际情况，因此对目标熵采用全局可变加权。式（7）中的U1（t）表示缺陷目标出现的累计概率，取值范围为［0，1］，缺陷占比越大概率越大，随着t增大呈现非线性增大。为符合加权因子的要求，加权因子W初定义为：

但为避免W分布中异常值的影响，用多项式回归拟合出一条近似W分布的平滑曲线P（t）；由于随着t增大，P（t）在t∈(0，220)减小得非常缓慢，加权效果较弱，为增加减小的加速度，将拟合曲线P（t）进行平方后作为目标熵的加权因子，即加权因子W最终定义为：

则式（10）可以改写为：

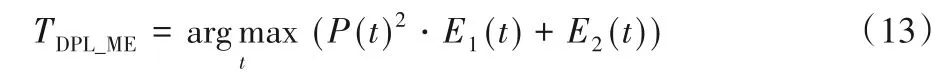
DPL_ME 结合了缺陷比例和全局可变加权因子，与ME相比，在保留缺陷完整信息情况下，获得了更小的阈值，消除了更多噪声，如图10（c）、（d）所示；并且能让剩余噪声尽可能降到钢轨表面伤损标准以下，以便在连通区域标记法中滤除，如图10（e）、（f）所示，本文方法将剩余噪声全部滤除，缺陷检测效果显著提升。

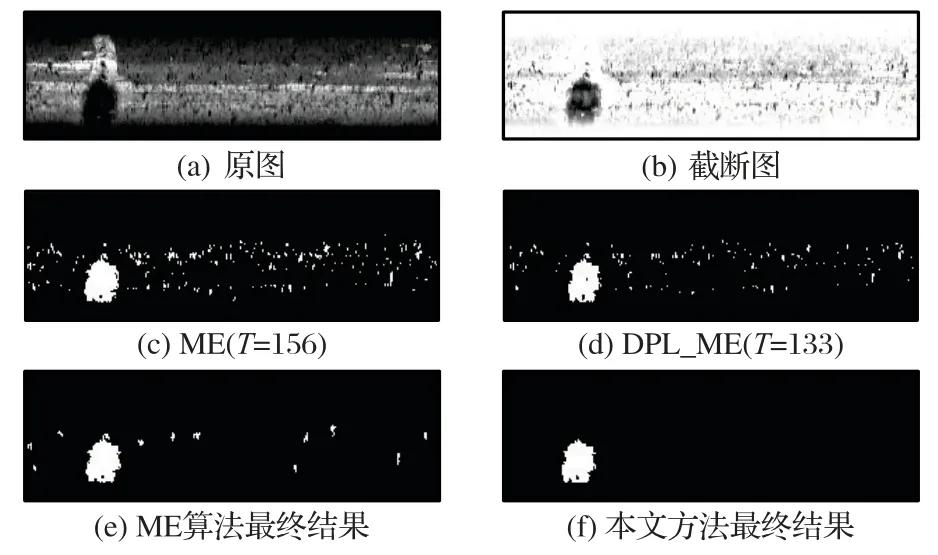
图10 ME和本文方法阈值分割结果对比Fig.10 Comparison of threshold segmentation results of ME algorithm and proposed method

2.4 连通区域标记法

从图10（c）、（d）可以看出，阈值分割后还存在一些面积比较小的缺陷，而这些小缺陷在短时间内不会危害列车行驶质量安全，可以判定为噪声。根据钢轨损伤标准［25］，面积大于80 mm2的缺陷就可能会对列车造成威胁，因此本文将面积大于80 mm2的连通区域判定为缺陷，否则就判定为噪声。步骤如下：

1）确定阈值分割图中所有的连通区域；

2）计算每个连通区域的面积；

3）去除损伤标准允许范围内的小区域。

如图10（e）、（f）所示，利用此法对分割后的二值图的缺陷区域进行统计、滤波，能有效去除轨面图像中暂不会危害铁路系统行车质量与安全的噪声，最终完成轨面缺陷检测。

3 实验与结果分析

仿真实验所使用的计算机硬件配置为：Inter Core i7 6700 CPU@3.40 GHz，8 GB内存，64位Windows 10操作系统，采用Matlab R2018a实现本文方法。

3.1 性能评价指标

为验证本文检测方法的有效性，选用错误分类误差（Mis-Classification Error，MCE）［26］、召回率（Recall rate，Rc）、精确率（Precision rate，Pr）［27］、平均值F-Score，以及方法运行时间5个评价指标进行评价。

1）MCE表示经过某种阈值分割方法分割后的二值图像被错误分类的比例，用来衡量单张图像的分割结果。它的取值范围为［0，1］，0表示没有被错分的情况，1表示完全被错分的情况。MCE的值越小，分割效果越好。MCE对于此类分割问题的定义为：

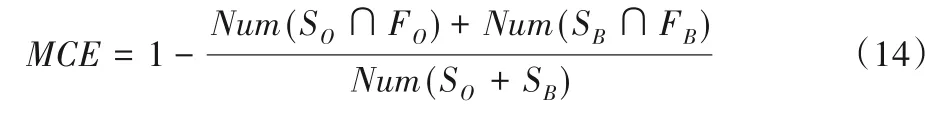
其中：SO和SB分别表示标准分割图像的目标区域和背景区域；FO和FB分别表示经过分割方法得到的目标区域和背景区域；Num(·)表示区域中像素点数目。

2）召回率Rc、精确率Pr和F-Score是模式识别和信息检索等领域最常用的指标，用来综合评价钢轨表面缺陷的识别、分类等检测结果。分别定义如下：

其中：TP表示正确识别目标的个数（True Positive）；FP表示错误识别目标的个数（False Positive）；TN表示正确未识别目标的个数（True Negative）。对于轨面缺陷检测来说，假如没能检测出部分缺陷，将很可能会危害列车的行车质量安全，严重时可能会造成事故，因此召回率相对更重要，故式（17）中的X取值为2（即：F2-Score），让召回率权重高于精确率。但是随着召回率上升，准确率会下降，因此如何达到二者的平衡是衡量缺陷检测方法的重要考量。

3.2 缺陷比例上界限分析

为了既保证尽可能真实的缺陷能够被检测，又能达到召回率和精确率的平衡，本文测试了不同缺陷比例上界限dp对本文方法性能的影响（dp=0.03，0.09，0.15，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9）。

图11 为不同dp下的轨面缺陷召回率和精确率的曲线。根据精确率曲线可以发现精确率随dp的增大而减小；根据召回率曲线可以发现dp＜0.3 时，召回率随dp的增大而增大；当dp＞0.3时，召回率随dp的增大而减小。这是因为缺陷比例上界dp控制着要过滤的信息量，当dp较低时，保留的信息较少，可能把一些缺陷也过滤掉；当dp较大时，虽然保留了更多的缺陷，但是同时也带来更多无缺陷信息和噪声，因此考虑到召回率和精确率的平衡把缺陷比例上界dp设为0.3。

3.3 鲁棒性分析

为验证本文检测方法的鲁棒性，针对钢轨表面多种复杂情况进行了实验。表2所示的是图12中的不同轨面的噪声干扰情况，包括不同光照（正常、强、不均、弱光照等）轨面，是否存在有阴影、锈迹、尘土等。

如图12 轨面1～4 所示，无论轨面在何种光照条件和噪声干扰下，在背景差分和缺陷比例上限阈值截断后，均能使轨面图背景变得均匀、缺陷目标凸显；随后在缺陷比例阈值分割中获得较优的阈值，对截断图进行二值化，消除轨面绝大部分噪声，保留真实缺陷。实验结果表明，本文方法对多种复杂情况的缺陷图像均取得了较为理想的检测效果。

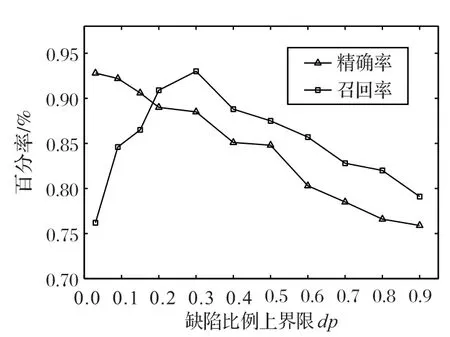
图11 不同缺陷比例对精确率和召回率的影响Fig.11 Influence of different defect proportion on precision rate and recall rate

表2 轨面图像噪声干扰情况Tab.2 Noise interference conditions of rail surface image

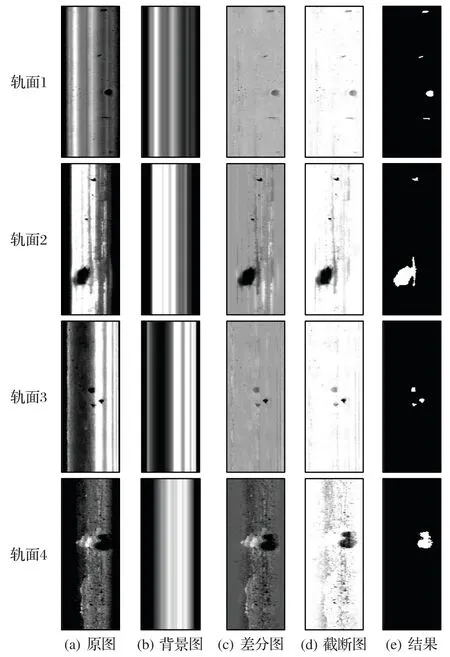
图12 多种复杂条件下的轨面缺陷检测结果图Fig.12 Result diagrams of rail surface defect detection under various complicated conditions

3.4 对比实验分析

本文从实验室收集整理的钢轨图像数据库中随机选取1 000 张带缺陷的钢轨图像进行测试，其中包含600 张至少存在一个缺陷的图像、400 张没有缺陷的图像（由于在实际运营的铁路中，大部分的铁路图像都是无缺陷的，因此加入无缺陷图像可以更好地反映实际情况），缺陷总数为740 个。将本文方法与目标方差加权的类间方差阈值分割方法WOV［15］、背景差分法BGD［18］、基于图像灰度梯度特征的轨面检测方法BGD2［19］，以及Otsu［16］、ME［24］等相关经典方法进行比较，采用召回率、精确率、加权调和平均F2-Score、平均错误分类误差和平均运行时间等指标进行定量分析对比。

如表3 所示，本文方法的召回率、精确率、加权调和平均值F2-Score均高于其他方法，平均错误分类误差MCE 值均低于其他方法，在缺陷检测耗时上，略高于除BGD2 外的其他方法。如图13 所示，Otsu、ME、WOV 这三种方法均是未对图像做其他预处理，直接在原轨面图像的背景对象和缺陷目标中利用某个平衡函数选取一个阈值进行分割，虽然简单，在相对友好轨面上能有一定的分割效果，但在实际轨面中，由于干扰因素较多，分割效果较差；BGD方法根据轨面图像沿列车行驶方向反射特性稳定的特性采用均值背景建模，对沿列车行驶方向反射特性稳定的轨面图像检测效果较好，但在有不规则阴影等噪声干扰时，容易把部分区域误检测为缺陷；BGD2 方法利用局部灰度和梯度变化，基于双边滤波器设计了一个平滑滤波器对背景进行建模，能够较好地检测裂纹和疤痕缺陷，但该方法参数过多，同一组参数无法适应形状各异及较多噪声干扰的轨面，检测时容易把噪声误判为缺陷。

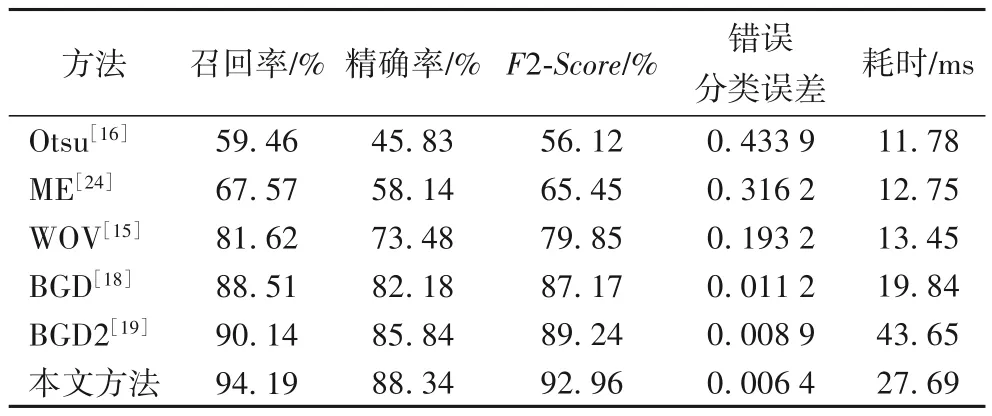
表3 不同方法在钢轨表面缺陷检测上的性能指标对比Tab.3 Performance index comparison of different methods on rail surface defect detection

本文方法利用灰度列均值和列中值进行快速背景建模，采用差分和缺陷比例上限阈值截断，最大限度地使原轨面背景均匀且凸显真实缺陷；随后利用缺陷比例，采用自适应加权因子，选择出一个较优的阈值二值化轨面图像，最后利用连通区域滤波器把缺陷面积低于钢轨损伤标准的区域判定为噪声去除，因此在多种环境因素干扰下（如光照不均、锈迹、阴影等）对多种缺陷（如裂痕、疤痕、磨蚀、擦伤等）均有较为满意的检测结果。对比分析结果显示了本文方法的优势，具有较好的应用价值。

图13 多种轨面缺陷检测方法结果对比Fig.13 Result comparison of various rail surface defect detection methods

4 结语

本文针对钢轨表面图像具有光照不均匀、可识别的特征有限、对比度低、反射特性易变等难点，提出了基于缺陷比例限制的背景差分钢轨表面缺陷检测方法。该方法具有以下优点：

1）DPL_BGD 不仅有效克服了光照不均，可利用特征有限等问题，且极大增强了轨面图像对比度。

2）DPL_ME基于缺陷比例限制和自适应加权因子得到比ME更小的阈值，在保留缺陷必要信息的同时，减弱诸如锈迹、污渍、尘土等噪声的干扰。

3）背景建模时仅计算轨面图像每列的灰度均值和中值，计算量小，速度快，满足实时性要求。

4）可变参数少，易于调节，可控性强。

本文方法召回率达到94.19%，精确率达到88.34%，加调和平均F2-Score值为92.96%，平均错误分类误差MCE 低至0.006 4，除耗时略高之外，其余评价指标均优于对比实验中的相关方法。

本文仅讨论了噪声与缺陷位置不重合的情况，该方法检测速度的进一步优化和噪声与缺陷位置重合情况的区分将是下一步研究的内容。