基于深度先验及非局部相似性的压缩感知核磁共振成像

宗春梅，张月琴，曹建芳，赵青杉

（1.忻州师范学院计算机系，山西忻州 034000；2.太原理工大学计算机科学与技术学院，太原 030024）

（*通信作者电子邮箱zongcm123@163.com）

0 引言

压缩感知核磁共振成像（Compressed Sensing Magnetic Resonance Imaging，CSMRI）是指通过观测的高度欠采样的k空间数据（图像的傅里叶变换，也称测量数据）重建原始图像［1］。在采样矩阵满足某种条件下，该技术能够从远低于奈奎斯特采样率的k空间数据中精确恢复原始图像［2］。CSMRI理论一经提出就以采样时间短、存储数据少的优点得到了学者们的关注。如何从少量的测量数据中高质量地恢复原始图像是CSMRI 领域面临的一大挑战。CSMRI 仅利用部分测量数据即包含少量信息的观测数据进行图像重建，该问题有无数个解，是一个病态问题。解决该问题的一个有效方式是利用图像固有的先验知识进行图像重建。近些年来，国内国外涌现出了大量的CSMRI 算法。根据算法利用的先验知识大致可以分为三大类：基于稀疏性的算法［3-5］、基于非局部相似性的算法［6-8］、基于深度先验的算法［9-12］。

基于稀疏性的算法是利用图像在变换域或者字典下的稀疏性进行图像重建。其中，稀疏性又可以分为全局稀疏性和局部稀疏性。全局稀疏性是指图像在梯度域、小波变换域、紧标架下的稀疏性，而局部稀疏性是指图像块在固定字典或自适应字典下的稀疏性。基于全局稀疏性的方法重建速度相对较快，但是重建质量有待提高。基于局部稀疏性的方法通过字典学习技术进行图像重建［5］，利用交替优化的方式在迭代过程中联合优化图像和字典。相较于基于全局稀疏性的方法，该类方法能够学习自适应字典，重建质量高，但成像速度相对较低。

基于非局部相似性的CSMRI 算法是利用非局部区域内图像块之间的相似性进行重建，本质是图像的当前块估计通过一定区域内的相似块加权得到。近些年，利用块匹配三维滤波（Block Matching and 3D Filtering，BM3D）高斯去噪器［13］隐式利用非局部相似性进行图像重建得到了学者们的关注。Eksioglu［6］利用BM3D 去噪器构建了去耦合的CSMRI 框架，该框架能够隐式地利用BM3D 去噪器包含的图像先验知识，即图像的非局部相似性及图像在三维小波变换下的稀疏性。Shi 等［7］利用BM3D 去噪器构建了正则化模型，并用于提升基于局部稀疏性的CSMRI 算法重建质量。实验结果表明该类方法能够获得较高质量的图像。

基于深度先验的算法是通过深度神经网络进行图像重建。Yang 等［9］利用交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）求解构建的CSMRI 优化问题，并将求解框架展开成网络，提出了ADMM-CSNet（Alternating Direction Method of Multipliers-Compressed Sensing Network）算法。ADMM-CSNet算法能够通过事先训练好的深度神经网络进行快速成像且取得较好的重建效果。基于深度先验的算法虽然能够取得较好的性能，但是该类直接训练端到端深度神经网络的方法泛化能力差，且不具可解释性。

上述算法虽然取得了较好的重建效果，但在低采样率时，重构质量仍然有提升空间。不同于上述算法，本文利用深度先验和非局部相似性进行压缩感知核磁共振成像。本文利用深度去噪器和BM3D 去噪器通过即插即用模型将这两种先验知识引入到图像重建中。受基于深度先验的稀疏表示模型［14］启发，本文提出基于两种去噪器的稀疏表示模型。该模型能够融合深度先验、图像的非局部相似性及图像在三维变换下的稀疏性进行图像重建。结合该模型与数据保真模型构建CSMRI 优化问题，利用交替优化的方式对该问题进行有效求解。本文利用多种先验知识进行成像期望得到高质量的图像重建。

1 基于稀疏性的压缩感知核磁共振成像

假设原始核磁共振图像为x∈RN，CSMRI 采样模型可描述为

其中：Fu∈Cm×N（m＜N）表示欠采样傅里叶编码矩阵，也即欠采样算子；ratio=m/N定义为采样率；y∈Cm表示观测的k空间数据即测量数据；n∈Cm表示高斯噪声向量。如何利用测量数据y重建原始图像x是CSMRI算法所要解决的问题。

基于全局稀疏性的CSMRI算法通常构建以下优化问题：

其中：ψ是某种全局变换；λ为正则化参数。||·||p表示lp范数：p=0时，即为l0伪范数，衡量对应向量中非零元素的个数；当p=1 时，||·||p为l1范数，表示对应向量中每个元素绝对值的和。上述优化问题可通过梯度下降法、变量分离法或其加速方法进行求解。基于全局稀疏性的方法能够快速进行图像重建，但由于全局变换是固定的，重建质量有待提升。

不同于上述算法，基于局部稀疏性的CSMRI 算法通常利用自适应字典进行重建。在重建过程中，通过估计图像学习自适应字典。该类方法通常构建以下优化问题［5］：

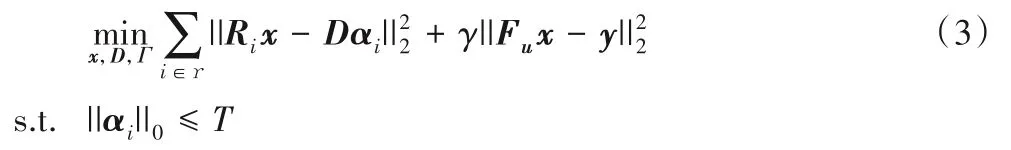
其中：ϒ是图像块索引的集合；Ri∈RB×N表示取块算子；γ是平衡参数；D∈CB×K表示待训练的块字典；αi∈CK表示图像块Rix在字典D下的表示系数；Γ是所有表示系数的集合；T为稀疏度。上述优化问题通常利用交替优化的方式分字典学习和图像更新两步进行求解。由于字典能够通过测量数据进行训练，学习的字典能够对重建图像自适应稀疏表示。基于字典学习的CSMRI 算法较基于全局变换的CSMRI 算法重建质量高。

为进一步提升重建质量，Eksioglu［6］利用BM3D 去噪器隐式利用隐含在BM3D 去噪器中的先验知识进行图像重建，提出了基于三维块匹配的核磁共振成像算法BM3D-MRI（Block Matching and 3D filtering-Magnetic Resonance Imaging）算法。该算法构建以下去耦合的CSMRI 优化框架（对于第t次迭代）：

其中：ΦBM3D表示BM3D 去噪器对应的解析稀疏算子［6］。式（4）可通过求导并令导数为0 获得闭式解，式（5）直接利用BM3D 去噪器近似求解。由于上述框架在优化过程中利用BM3D 去噪器对估计图像进行去噪处理，该框架能够隐含地利用非局部相似性。

受上述算法及基于深度先验的稀疏表示模型［14］启发，本文通过BM3D 去噪器和深度去噪器相结合，提出融合多种先验知识的CSMRI 算法。本文构建了基于多种去噪器的稀疏表示模型，该模型能够将多种去噪器蕴含的先验知识融合到图像重建中。多种先验知识的利用能够提升低采样率下的重建质量。

2 基于多种去噪器的稀疏表示模型

如何利用多种先验知识进行CSMRI 是本文解决的一个关键问题。本文利用两种不同的去噪器构建稀疏表示模型以利用多种先验知识。传统稀疏表示模型假定图像x在标架或某种变换W下是稀疏的，通常构建以下优化模型以求解稀疏表示系数［15］：

其中参数η控制稀疏程度。对于任意变换W，上述优化模型可以通过迭代阈值方法求解。为了降低计算复杂度，本文将紧约束施加到标架W上，即W为紧标架WTW=I。基于紧标架的优化问题（6）可直接通过简单的阈值方法求解。图像经过BM3D 去噪器的滤波图像在紧标架下的表示系数与原始图像在同一紧标架下的表示系数应该是近似的，两个系数向量的差值应是稀疏的。基于该认识，本文构建基于多种去噪器的稀疏表示模型，优化模型可表示为：

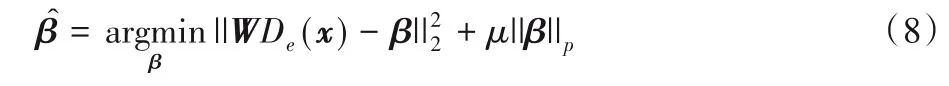
其中：De(x)表示利用去噪器对图像x进行滤波；μ表示稀疏正则化参数，用以控制滤波图像在紧标架下的稀疏程度。De(x)可以是单个去噪器，也可以是多种去噪器的加权求和即表示第j个去噪器对图像进行滤波以后的图像）。文献［14］指出利用不同的高斯去噪器可以将不同的先验知识引入到图像重建中。本文利用两种去噪器构建该模型，即深度去噪器与BM3D 去噪器。在这种情况下，滤波图像可表示为。其中，Deep(x)表示利用深度去噪器对图像进行滤波，BM3D(x)表示利用BM3D 去噪器对图像进行滤波。本文联合采用这两种去噪器，试图融合两种去噪器在去噪或滤波过程中利用的先验知识进行图像重建。深度高斯去噪器利用深度先验进行图像去噪，利用该去噪以将深度先验引入到图像重建中。深度去噪器通常未充分利用图像的自相似性，BM3D 去噪器弥补了该不足，该去噪器通过利用非局部区域内的相似性先验知识进行图像去噪。本文利用这两种去噪器进行联合去噪或滤波以期望利用深度先验和非局部相似性先验的互补性进行高质量图像重建。

式（8）可通过对滤波图像在紧标架下的表示系数进行阈值处理求解。如果p=1，则，此时表示阈值为的软阈值算子，定义为T[·，ε]=soft{·，ε}=sign(·)max(|·|-ε，0)，sign(·)为符号函数，max(·)为取最大值算子。如果p=0，则，此时表示硬阈值算子，定义为：如果，否则。需要指出的是，阈值算子操作是逐元素进行的，因此上述对向量的处理是对每一元素进行阈值处理。

构建的上述正则化模型R(x)是一个包络函数，可以直接作为正则项引入到成像的优化模型中。式（9）中的第一项表示图像在紧标架下的表示系数近似为α，第二项表示该系数逼近于辅助系数向量。其中该辅助系数向量的更新能够通过两种去噪器将深度先验、非局部相似性及三维变换下的稀疏性隐式地进行利用。由于式（9）中的辅助系数向量可通过求解式（8）获得，故基于BM3D 去噪器的稀疏表示正则化模型可写成以下简洁的形式：

构建的正则化模型（10）具有以下优点：

1）有效。该正则化模型能够通过多种去噪器利用多种互补先验知识进行图像重建，多种先验知识有益于图像重建；

2）灵活。该模型的灵活性主要体现在以下两个方面：第一，去噪器可以换成其他有效的去噪器以利用不同的先验知识进行图像重建；第二，该正则化模型可用于其他成像应用，不局限于压缩感知核磁共振成像。

3 融合深度先验及非局部相似性的CSMRI

本文利用基于两种去噪器的稀疏表示模型进行压缩感知核磁共振成像以解决现有CSMRI 算法重建质量低的问题，构建以下优化模型：

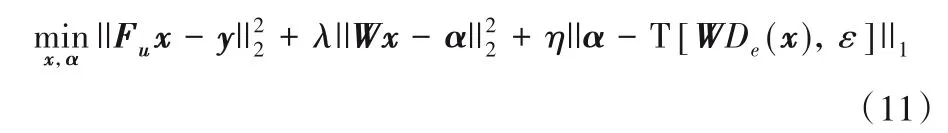
式（11）代价函数中：第一项为数据保真项，保证重建的图像与测量数据y相匹配；第二、三项为本文构建的基于多种去噪器的稀疏表示模型。由于上述代价函数采用l2范数和l1范数，如果固定辅助系数向量T[WDe(x)，ε]，所对应的优化是一个凸优化问题。然而，由于阈值算子（阈值算子是非凸的）和多种去噪器（去噪器可看成去噪函数，通常是非凸的）存在于最后一项，上述优化问题在考虑x和α联合优化时，该问题是一个复杂的非凸优化问题。为了对其进行有效求解，本文假设滤波图像De(x)近似于估计图像的滤波图像De(x(t-1))，即De(x)≈De(x(t-1))。基于该假设，优化问题（11）可改写为（对于第t次迭代）：

利用交替优化的方法求解上述优化问题，对于第t次迭代，分为以下两步对问题（12）进行求解：

1）系数更新步骤，固定估计图像x(t-1)，更新稀疏系数α(t)的子问题为：

上述优化问题可通过软阈值算子进行求解：

实验结果表明，T[·，ε1]采用硬阈值算子成像效果优于利用软阈值算子，因此本文采用硬阈值算子。对滤波图像在紧标架下的表示系数进行硬阈值处理，得到辅助系数向量T[WDe(x(t-1))，ε1]。

2）图像更新步骤，固定稀疏系数α(t)，更新图像x(t)的子问题为：

对式（15）中的代价函数求导，并令导数为零：

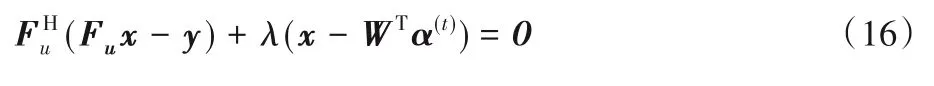
傅里叶变换矩阵F∈CN×N通常为酉矩阵，满足FHF=I。根据这一等式，式（16）可改写为：

其中：Fx(t)(kx，ky)表示在位置(kx，ky)的更新值；Ω是被采样的k空间数据的集合。最后对Fx(t)进行傅里叶反变换，获得最终图像重建结果。

交替优化稀疏系数与图像直到达到终止条件可以得到优化问题（11）的一个近似解。本文算法如下：

4 实验与结果分析

为了验证本文算法的有效性，本文采用了6 幅大小为256 × 256 的核磁共振图像作为测试图像进行压缩感知核磁共振成像实验，测试图像分别为Brain、Shoulder、Bone、Head、Bust、Brain2。采用伪随机采样算子对k空间数据进行欠采样，图1给出了采样算子和6幅原始图像。所有算法均在配置为Core i7-7700 主频3.6 GHz CPU，内存8 GB 的PC 上进行测试，软件平台为Windows 10 64 位操作系统，Matlab 2018b。为了模拟更真实的采样环境，本文对采样值施加噪声标准差为σ=1 的噪声。本文算法在不同采样率情况下与基于小波树稀疏性的核磁共振成像算法WaTMRI（Magnetic Resonance Imaging with Wavelet Tree sparsity）［4］、基于字典学习的核磁共振成像算法 DLMRI（Dictionary Learning for Magnetic Resonance Imaging）［5］、基于字典更新及块匹配和三维滤波的核磁共振成像算法（Magnetic Resonance Imaging based on Dictionary Updating and Block Matching and 3D filtering，DUMRI-BM3D）［7］、BM3D-MRI 算法［6］、广义近似消息传递去噪算法DAMP（Denoising Approximate Message Passing）［8］进行对比，对比算法均采用软件包中给出的默认参数。本文分别从客观角度和主观视觉角度对测试算法进行对比。采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）作为评价重建质量好坏的客观标准，主观视觉评价则计算特征相似性（Feature SIMilarity，FSIM）［16］，同时给出各个算法的部分重建图像进行对比。PSNR 值和FSIM 值越大表明重建图像视觉效果越好，重建质量越高。

在实验中，本文的深度去噪器选用近些年比较优秀的深度去噪器FFDNet（Fast and Flexible Denoising convolutional neural Network）［17］。输入去噪器的噪声标准差采用BM3DMRI 算法给出的非线性构建方法［6］。假设该方法计算的标准差为σ，为实现较好的重建效果，输入BM3D与FFDNet去噪器的噪声标准差分别为6σ、3σ。正则化参数λ、阈值ε1及ε2均采用PSNR 值最大的准则进行调节，对于某一幅测试图像，固定一个参数，去调节另一个参数使得获得的PSNR 值最大。当调到最大效果时，固定该参数，去调节另一个。阈值ε1与ε2应与估计图像中的噪声标准差有关，经验表明，当λ=0.01、ε1=0.5σ、ε2=5σ时，图像重建效果最好。当参数调整好以后，利用这套参数对不同采样率下、不同图像进行核磁共振成像。紧标架选用离散余弦变换并使用文献［14］公布的默认参数。为了公平比较，提出的算法对于不同的采样率选用同一套参数。为了说明多种互补先验的有效性，本文将仅利用FFDNet 去噪器的方法作为基准算法，简记为CSMRIFFDNet。

图1 采样算子和原始图像Fig.1 Sampling operator and original images

表1 给出了在采样率为0.02、0.06、0.09 及0.13 的情况下测试算法的PSNR 值（由于版面限制，本文仅给出5 种具有代表性的测试算法结果），从中可以看出：1）对于多数情况，本文算法的PSNR 值最高；2）以Brain 图像为例，在采样率为0.02 情况下，本文算法重构图像的PSNR 值比DUMRI-BM3D算法、BM3D-MRI 算法、DAMP 算法及CSMRI-FFDNet 算法分别提高了1.05 dB、0.45 dB、0.85 dB 及0.34 dB；3）在低采样率下，本文算法仍然能够重构出较高PSNR 的图像；4）利用两种去噪器的本文算法优于仅利用FFDNet 去噪器的CSMRIFFDNet 算法。CSMRI-FFDNet 算法利用了深度先验，重建平均PSNR 值优于其他对比算法。深度先验并未考虑图像非局部区域的相似性，由于本文算法能够利用深度先验与非局部相似性进行图像重建，因此本文算法优于仅利用深度先验的CSMRI-FFDNet算法。

为了进一步衡量本文算法主观视觉的优点，表1 给出在不同采样率下测试算法获得的FSIM 值。从表1 中可以看出，本文算法对于不同图像、不同采样率都能够获得最高的FSIM值，也就意味着视觉效果最好。图2 给出了测试算法对图像Head的重建结果，从重建图像中可以看出：WaTMRI的重建质量最差、最模糊，含有大量的噪声；DLMRI 算法重建图像消除了部分噪声，但仍然丢失了大量细节信息，并且重建图像具有块效应；DUMRI-BM3D 算法、BM3D-MRI 算法及DAMP 算法消除了噪声，但是重建图像丢失了部分细节信息，具有明显的伪影效应；而本文算法消除了伪影，保留了大量细节信息，视觉效果最好。

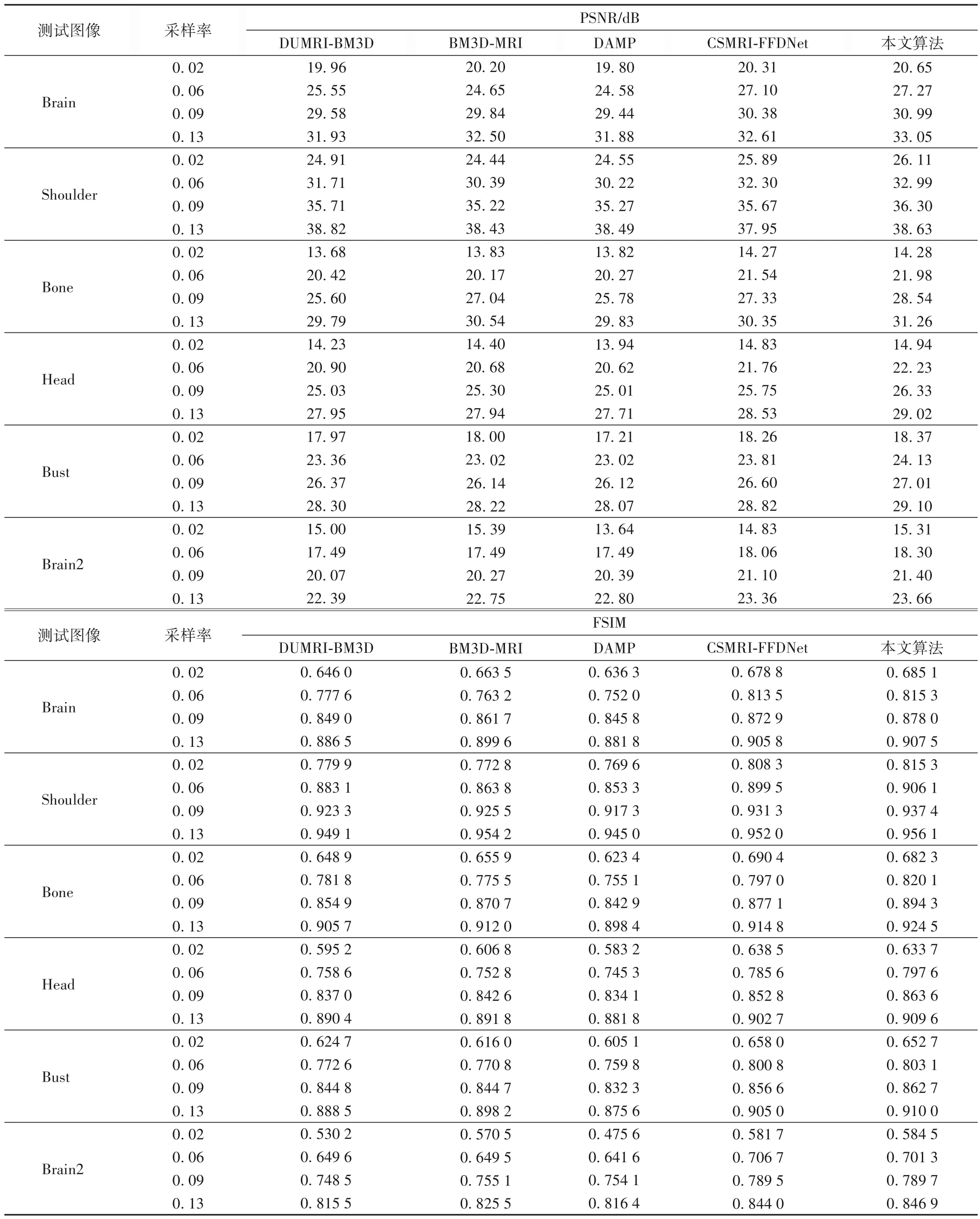
表1 不同算法PSNR值和FSIM值比较Tab.1 Comparison of PSNR and FSIM values of different algorithms

为了衡量算法的成像速度，表2 给出了测试算法的平均运行时间，是测试算法对4 种采样率、6 幅图像的运行时间平均值。从表2 可以看出，仅利用全局变换的WaTMRI 算法耗时最少，利用字典学习进行成像的DLMRI 算法用时最多。DUMRI-BM3D 算法利用字典更新和BM3D 去噪器进行成像，因此成像时间相对较长。本文算法的运行时间较WaTMRI算法、BM3D-MRI算法及CSMRI-FFDNet长。这是因为本文算法利用了稀疏表示和BM3D 去噪器。为提升成像速度，本文算法可通过并行计算进行加速。虽然本文算法比这3 种算法耗时长，但本文算法重建质量高于这3 种算法，更加适用于低采样率下对重建质量要求高的场合。

图2 测试算法的Head重建图像（采样率为0.06）Fig.2 Reconstructed head images by different test algorithms（sampling ratio of 0.06）

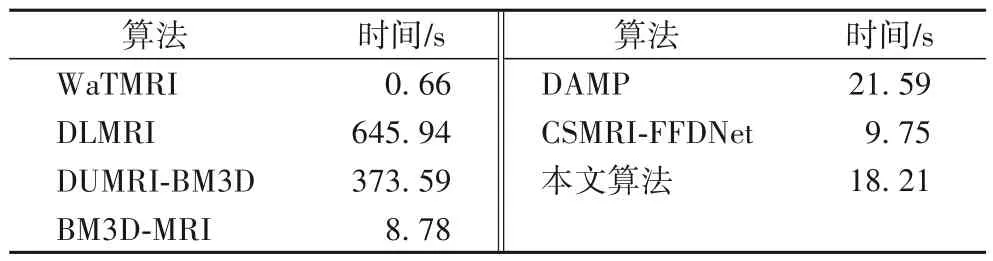
表2 不同算法的运行时间比较Tab.2 Running time comparison of different algorithms

5 结语

本文针对深度先验和非局部相似性的互补性，利用基于多种去噪器的稀疏表示模型，提出了融合两种先验知识的压缩感知核磁共振图像重构算法。该算法将基于多种去噪器的稀疏表示模型结合到CSMRI 的代价函数中，利用交替优化方法有效地求解了所对应的优化问题。实验结果表明，提出的算法能够在低采样率下获得较高的重建质量，且两种先验知识的融合能够提升图像的重建质量。如何加速本文算法是以后的研究方向。