一个R2 上含双曲函数核的Hilbert 型不等式

有名辉，孙霞

（浙江机电职业技术学院 数学教研室， 浙江 杭州310053）

0 引 言

Ω 为实数集R 中的L可测集,θ(x)是定义在Ω上的非负L可测函数,p＞1,

特别地, 当θ(x)=1 时, 上式可简记为Lpθ(Ω)=Lp(Ω)。

若f,g≥0,f,g∈L2(0,∞), 则 有 以 下 著 名 的Hilbert 不等式[1]:

其中π 是满足式(1)的最佳常数因子。

自提出Hilbert 不等式以来的100 余年中,通过对核函数(x+y)-1的演化、类比和推广，加上其对应的离散及半离散形式，已建立了大量类似于式(1)的Hilbert 型不等式[2-9]，这些不等式在分析学中已有广泛的应用[10]。

文献[11-14]研究了以双曲函数为核函数的Hilbert 型不等式，其中,文献[11-12]分别建立了不等式：

在式(2)和式(3)中, 均有μ(x)=ν(x)=x-3。

显然，不等式(2)和(3)的积分核函数在R2中不恒为正, 不宜做全平面推广。考虑到当α,β＞0 时,sinh(αt)与csch(βt)在实数域R/{0}上同号，故笔者探究全平面上核为sinh(αxy)csch(βxy)的二重积分不等式，并借助正切函数的有理分式展开,建立最佳常数因子与正切函数偶数阶导数相关联的Hilbert 型不等式。

1 定义及引理

定义1[15]对u＞0，定义第二型欧拉积分，即Γ函数：

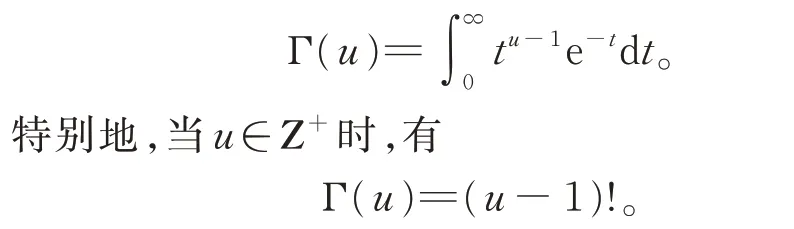
引理1 设|a|＜1，n∈N，φ(t)=tant，则

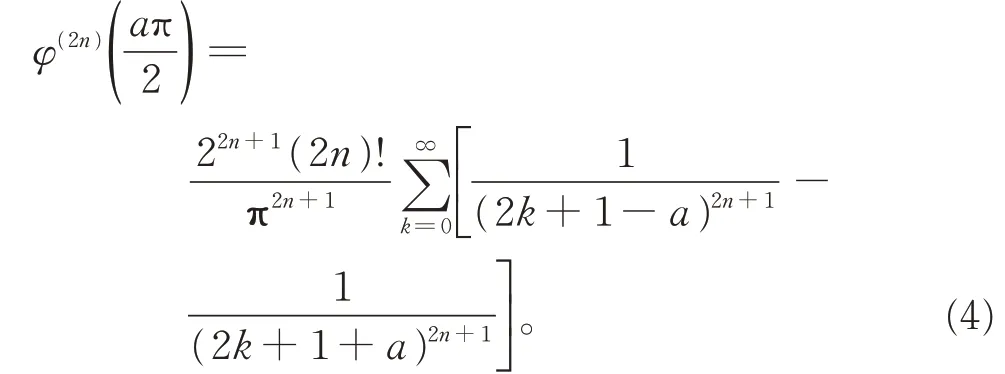
证明φ(t)=tant的有理分式展开如下[15]：

引理2设β＞α＞0,λ≥0,

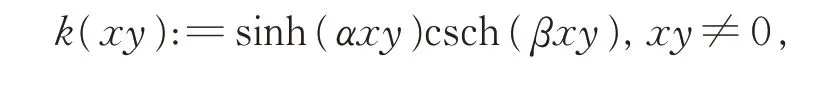
将csch(βt)展开成无穷级数，可得

通过简单的代换，易得

将式(16)代入式(9)，可得式(7)。

类似地，可得式(8)。

证毕！

引理3,β＞α＞0,λ≥0,k(xy)及C(α,β,λ)由引理2 定义, 函数fε(x)和gε(x)(ε为充分小的正数)定义如下：

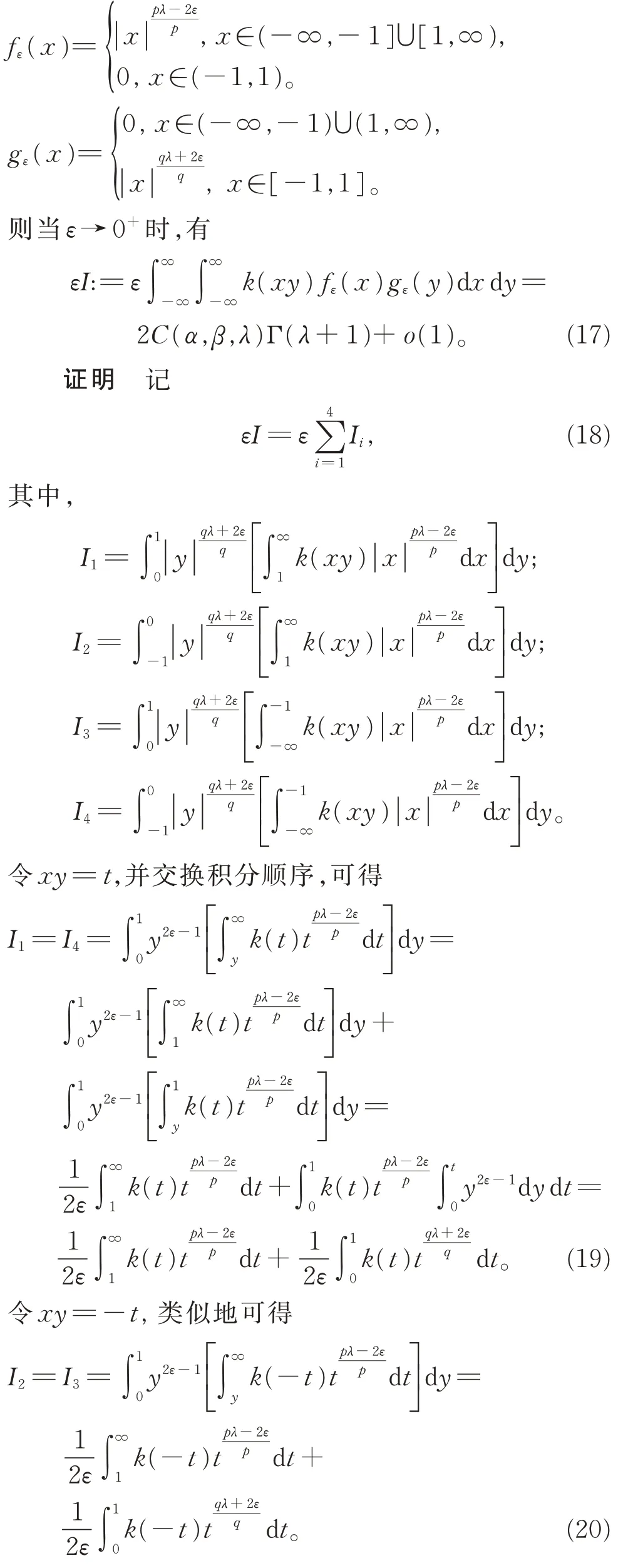
将式（19）和式(20)代入式(18)，可得

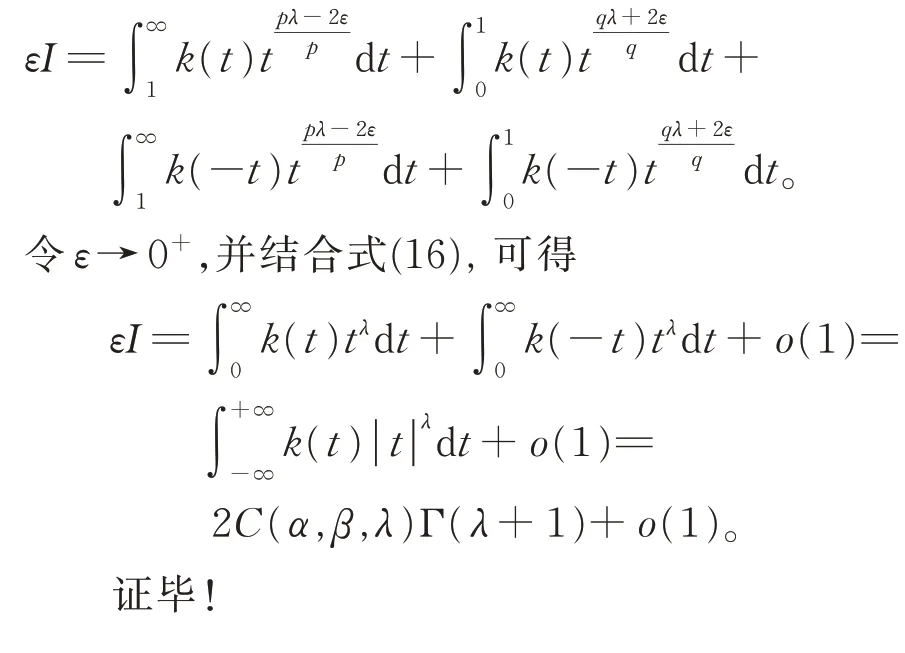
2 主要结果及证明

定理11，β＞α＞0,C(α,β,λ)如引理2 定义,λ≥0,φ(x)=tanx,n∈N,

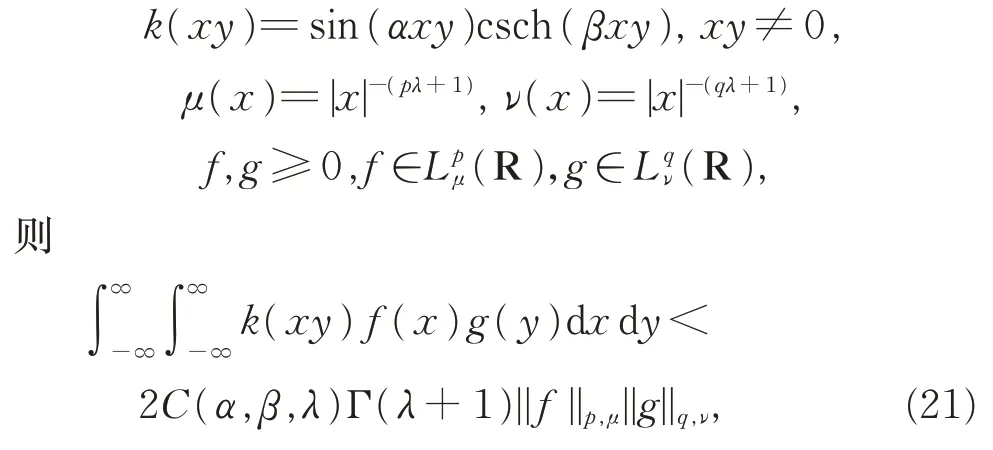
特别地, 当λ=2n时, 式(21)可转化为

证明由Hölder 不等式，结合引理2，得

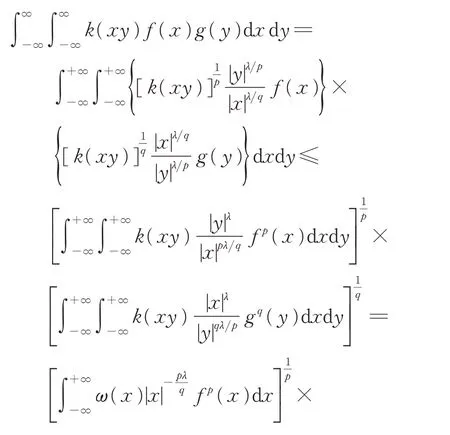
如果式(23)取等号，那么有不全为零的实数A1与A2,满足

与f∈(R)矛盾。故式(23)取严格不等号。

下证式(21)中的常数因子2C(α,β,λ)Γ(λ+1)为最佳值。事实上，若此常数因子不为最佳值，则必存在更优实数k(0 ＜k＜2C(α,β,λ)Γ(λ+1))，使得式(21)中的常数因子替换为k后不等式仍成立。即

用引理3 中定义的fε和gε分别替代式(24)中的f和g，则有

将 引 理3 的 结 果 代 入 上 式,并 令ε→0+，则 有k≥2C(α,β,λ)Γ(λ+1),矛盾。因此式(21)中的常数因子为最佳值。

特别地, 当λ=2n时, 根据引理2 中C(α,β,λ)的定义以及引理1 的结论, 不难得到式(22)。

定理1 证毕。

在定理1 中,令β=2α,λ=1, 并注意到

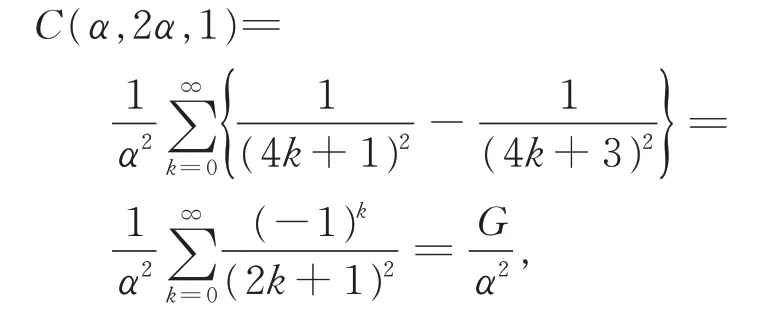
其中G=0.915 965 59…，为Catalan 常数。由此不难得到以下推论。

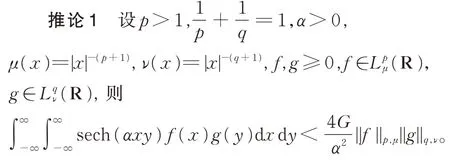
在定理1 中,令β=2α,λ=2n,由式(22)，又可得到另一个核为双曲正割函数的Hilbert 型不等式。

特别地, 若α=1，n=0，则μ(x)=ν(x)=|x|-1, 此时式(25)可化为

特别地, 若α=1，n=0，则μ(x)=ν(x)=|x|-1, 注意到tan=-1，此时式(26)可化为

此外, 令β=3α,β=,…,还可得到一些很容易计算常数因子的Hilbert 型不等式，在此不一一赘述。