短区间中整数及其逆的分布

赵艳，吕星星

（1.西安文理学院信息工程学院，陕西西安710068； 2.西北大学数学学院，陕西西安710127）

0 引 言

同余理论不仅极大丰富了初等数论的内容，而且推动了数论的发展。正因如此，不少学者对一些特殊整数的同余性质进行了研究，获得了一系列漂亮的结果！例如，1640 年，Fermat 得到了著名的Fermat 小定理[1]:当p为素数时，对于任意的整数a，有同余式：

1760 年，Euler 进一步推广 了Fermat 的结果，得到了著名的Euler 定理：设m≥2, (b,m) =1，则有同余式：

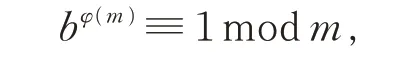
其中，φ(m)为Euler 函数，表示不超过m且与m互素的正整数的个数。

1770 年，Wilson 利用多项式的同余性质给出了一个包含阶乘的同余式，也就是著名的Wilson 定理：若p为素数，则有同余式：

以上同余式在初等数论教材中都可以找见，也可参阅文献[1]。

此外，1997 年，数学家VANHAMME[2]利用计算机得到与超几何级数恒等式p-adic 相关的13 个同余式，涉及p-adic 伽马函数，并给出了其中3 个同余式的证明，其中最典型的为

其中，p为奇素数。

值得一提的是，南京大学孙智伟教授及其团队基于其所做的大量研究工作，提出了不少涉及同余式以及恒等式的猜想。例如，PAN 等[3]通过研究得到同余式：

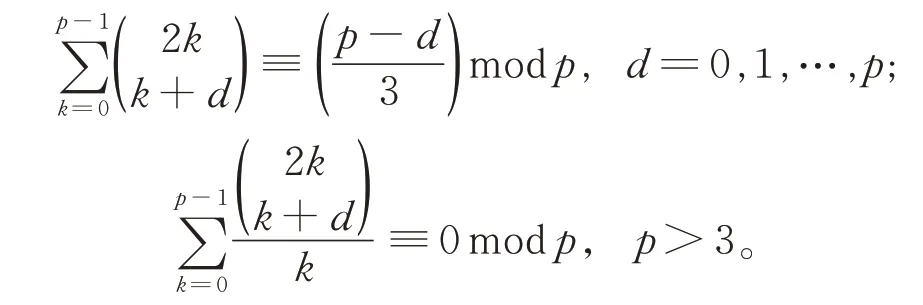
ZHAO等[4]对Catalan数进行了研究，并证明了同余式：

DUAN 等[5]给出了Bernoulli 多项式的同余式：设m是非负整数，对任意整数h,均有

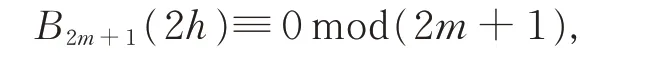
HOU 等[6]在研究Euler 函数和DirichletL-函数时得到了同余式：

相关研究很多，不再一一列举，有兴趣的读者可以参阅文献[7-13]。

2019 年9 月，浙江大学蔡天新教授在西北大学访问期间所做的报告中提到一个新的同余式：

同时，他提出一个有意义的猜想：设p是一个奇素数，除p=3,5,7 及13 外，至少存在1 组整数1＜i,j＜，使 得 他 们 满 足 同 余 式i⋅j≡1 modp,即μ(p)≥1。

笔者认为这一猜想属于整数及其逆在素数p下的分布问题。确切地说，属于短区间中整数及其逆在素数p下的分布问题。基于此问题，本文利用初等方法、三角和性质以及Kloosterman 和估计开展了研究，并用2 种不同的方法证明了上述猜想是正确的，即证明了以下2 个定理。

定理 1设p是一个奇素数，那么当p≠3,5,7,13 时，至少存在1＜j＜1＜使得j⋅-j≡1 modp。

定理2设p是一个奇素数，M是正整数且满足1＜M＜p，则有渐近式：

显然，定理1 和定理2 各有千秋，分别从不同角度刻画了蔡天新的猜想。定理1 证明了蔡天新的猜想，但只给出猜想中正整数的存在性，并没有说明正整数的数量。当p充分大时，定理2 给出了更短区间上μ(p)的渐近式，也就是说，此时猜想中的正整数不仅存在，而且有很多！因为对任意给定的正数ε，2 是一个非平凡的渐近式。受经典Kloosterman 和估计的限制，在定理2 中须规定M＞，此外，M的下界可否进一步改进也是一个值得探讨的问题！

1 定理的证明

本节证明中用到的初等数论相关知识可参阅文献[1]，此处不再赘述。首先利用初等方法证明定理1。

对于任意奇素数p，显然有p=4n+3 或p=4n+1。下面分别讨论此2 种情况：

（II）当p=4n+1 时，可将n用5 的完全剩余类分为以下5 种情况：

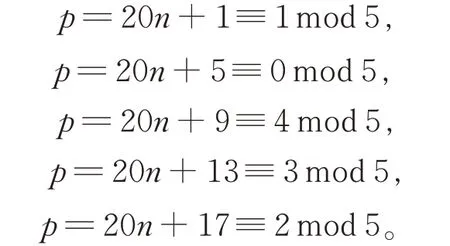
（i）当p=20n+1 时，设n=l⋅2h，h≥0,l为 奇数，此时有

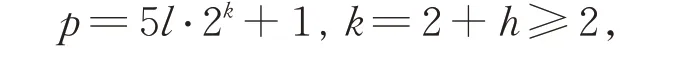
注意到5l(2k-1) +1 为偶数，所以有

（ii）当p=20n+5 时，p为素数，此时只有n=0,p=5，经检验不存在1≤j,-j≤2 使得

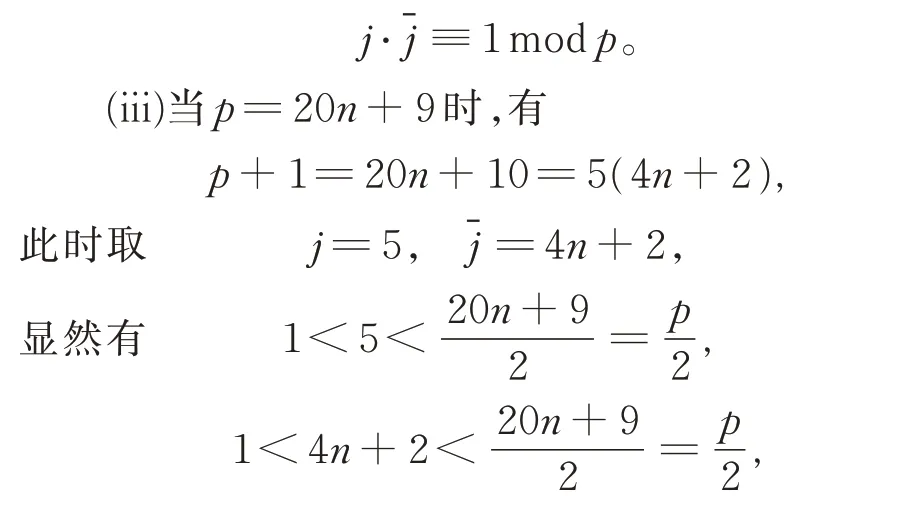
于是假设n≥1，注意到

综合以上5 种情况，定理1 得证。

下面利用三角和性质以及Kloosterman 和估计证明定理2。

对任意整数n，有三角恒等式:

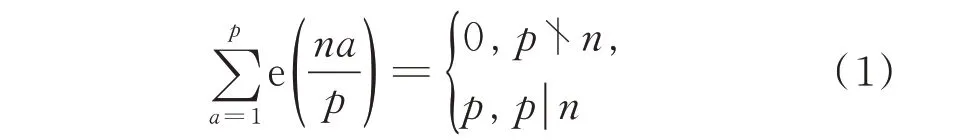
及Kloosterman 和 估计[14-15]：

其 中，e(y) =e2πiy,(m,n,p)表 示 整数m,n,p的 最 大公约数。

设N(M,p)为区间[1,M]内满足1＜M及≡1 modp的j的个数，则由式（1），可得

定理2 得证。