浙江大学函数论学派1928—1950 年的学术贡献

薛有才，刘炜，彭佳

（1.浙江科技学院理学院，浙江杭州310023； 2.浙江特殊教育职业学院，浙江杭州310023）

0 引 言

浙江大学数学学派是民国时期形成的以陈建功、苏步青等为代表的我国著名数学学术团体之一。该团体在函数、微分几何、代数、数学史等领域做出了巨大贡献。本文主要以其在傅里叶级数方面的工作来讨论浙江大学函数论学派在1928—1950年的贡献，以使读者了解他们所做的工作。

傅里叶级数（Fourier series）是一种特殊的三角级数，由法国数学家傅里叶（J.B.J. Fourier）提出并发展为著名的傅里叶级数理论。我国现代数学的先驱陈建功、王福春、周鸿经、卢庆骏、徐瑞云、程民德、项黼宸等为傅里叶级数在我国的传播与研究做出了巨大贡献。其中，贡献最大的是陈建功，他在1928年发表著名论文：On the class of functions with absolutely convergent Fourier series[1]，其中关于三角级数在区间上绝对收敛的充分必要条件被誉为“陈-哈代-李特尔伍德定理”，这是我国现代数学取得的第一个具有世界水平的成果，标志着我国现代数学开始向世界水平冲击。数学家李仲珩于1947 年在总结我国现代数学发展时指出：“走分析这条路，是陈建功和熊庆来两位领导起来的。其中成就最大的要算傅里叶级数的研究者，尤以王福春为难能可贵。”[2]

1 傅里叶级数在我国的研究概况

1.1 研究论文

据不完全统计，1928—1950 年，我国学者在国外学术期刊上发表的傅里叶级数相关学术论文共93 篇，在国内学术期刊上发表的相关学术论文有34篇[3-5]。其中，在国外学术期刊上发表论文的作者有10 人，分别为陈建功21 篇，王福春34 篇，程民德15篇，卢庆骏9 篇，周鸿经8 篇，徐瑞云2 篇，项黼宸、冯乃谦、朱良璧、周怀衡各1 篇；在国内学术期刊上发表论文的作者有12 人，分别为陈建功7 篇，程民德6篇，项黼宸5 篇，周鸿经3 篇，王寿仁3 篇，王福春2篇，卢庆骏2 篇，魏德馨2 篇，吴有训、王季同、曾炯、范会国各1 篇。涉及傅里叶级数研究的作者共16人，国内外发表论文127 篇。其中，属于浙江大学函数论学派的研究者有10 人，共发表论文109 篇。

此间，我国学者在国外发表数学学术论文共910 篇，参与工作的作者147 人。如此，傅里叶级数研究论文占比为11.41%，学者占比为8.61%；而浙江大学函数论学派在国外发表傅里叶级数相关学术论文共84 篇，占国外傅里叶级数相关论文发文总数的90.32%，占数学学科国外发文总数的9.23%；国内发表傅里叶级数相关论文25 篇，占国内傅里叶级数相关论文发文总数的73.53%。

1.2 研究专著

1929年，陈建功以傅里叶级数系列研究成果成为在日本取得理学博士学位的第一位中国学者。他怀着振兴我国现代数学的理想，婉言谢绝导师的留校建议，决定回国。同时他遵循导师另一项建议——写一部关于三角级数的专著。当时，他对国际上有关三角级数研究概况已烂熟于心，综合自己的研究成果和当时国际上傅里叶级数的最新研究进展，用日文撰写了专著《三角级数论》，交由日本著名的岩波书店出版。该书分2编，第1 编为积分概论，主要介绍三角级数的预备知识，包括点集与积分；第2 编为傅里叶级数，共7 章，其中，第1 章介绍一般三角级数理论，其余6 章介绍傅里叶级数理论。该著作的出版时间比J.D.塔·玛拉因的《傅里叶级数》早3 年，比波兰著名数学家A.Zygmund 的名著《三角级数》及S.Kaczmarz 和H.Steinhaus 合著的《正交级数论》第1 版早5 年，仅比L.Tonelli 的《三角级数》晚2 年。可以说，陈建功的《三角级数论》是世界上最早的也是最著名的有关傅里叶级数的专著之一，数十年后该书仍被列为日本最重要的基础数学参考书之一。l984 年出版的《日本数学100 年史》将《三角级数论》作为日本昭和前期实变函数论领域的一项重要成果。

1.3 学术奖励

1940 年5 月，民国教育部颁布了《著作发明及美术奖励规则》。奖励范围分三类：一是著作类，二是研究发明类，三是艺术类。奖励时段为在最近三年内完成的成果[6]。奖励等级设一等奖、二等奖、三等奖[7]。

经民国教育部学术审议委员会评定，从1941—1947 年，民国政府共颁发六届学术奖励。数学学科共有14 位（15 人次）获得15 项奖励[8]。其中，一等奖4 项，二等奖3 项，三等奖8 项（包括胡世华获得的哲学类三等奖1 项）。除此之外，机电专家吴大榕、建筑专家柴方荫和王仁权分别获得3 项应用数学成果获；陆德慧因其在珠算方面的研究获得1 项鼓励性质的“奖助”。获奖领域包括傅里叶级数（5 项）、微分几何（4 项）、代数与数论（4 项）、应用数学（3 项）、概率论与数理统计（2 项）、珠算（1 项，获奖助）[7]。其中，有关傅里叶级数的获奖项目包括

第二届（1942 年度）：周鸿经以《傅氏级数》（论文）获二等奖。

第三届（1943 年度）：陈建功以《傅氏级数之蔡查罗绝对可和性论》（论文）获一等奖，王福春以《傅氏级数之平均收敛》（论文）、卢庆骏以《傅氏级数之求和论》（论文）获三等奖。

第六届（1946 年度）：王福春以《三角级数之收敛理论》（论文）获一等奖。

在18 项数学类学术奖励中，傅里叶级数领域获得5 项，占比27.8%。其中，浙江大学函数论学派获奖4 项，占所有奖项的22.2%；在数学学科的4 项一等奖中，3 项由浙江大学获得（另一项由苏步青于1942 年获得），其中傅里叶级数领域获得2 项，占比50%。以上数据以及1.1 节中的2 组数据充分说明了浙江大学函数论学派在我国现代数学发展历程中的带头作用。

1.4 傅里叶级数领域获得的博士学位

博士学位论文是学者学术研究水平的体现。民国时期，开展傅里叶级数相关研究并获得数学博士学位的学者共有4 位，全部为浙江大学函数论学派成员。

（1）陈建功，1929 年获日本东北帝国大学博士学位，导师为藤原松三郎，博士论文题目为《三角级数论》，取得系列研究成果。

（2）徐瑞云，1940 年获德国慕尼黑明兴大学博士学位，导师为世界著名数学家C.Carthéodory，博士论文题目为Über die Fourievsche entwicklung der singulären funktion bei einer Lebesguesehen ehen zerlegung。

（3）卢庆骏，1948 年获美国芝加哥大学数学研究院博士学位，导师为世界著名三角级数大师A. Zygmund，博士论文题目为Note on the properties of Fourier cefficients。

（4）程民德，1949 年获美国普林斯顿大学博士学位，导师为世界著名数学家S.Bochner，博士论文题目为On the uniqueness theorem of multiple trigonometrical series。

2 傅里叶级数在我国的教育概况

我国现代数学教育起步较晚，但发展较快。傅里叶级数在我国的教育主要有3 种形式：大学本科教育、研究生教育、研究讨论班教育。

2.1 大学本科教育

从傅里叶级数的本科教学中可以看到，20 世纪30 年代，部分大学已开设级数理论课程，其中包含傅里叶级数理论。例如，北京大学数学系在1931—1935 年各年度课程表[9]中，已有奥斯古德(W. Fogg Osgood，1864—1943)开设的函数各论（乙）课程，并明确标注包含势函数、三角级数、带球函数、Bessel函数等。该课程将欧美数学家的3 种原著列为参考书，如美国数学家W. E. Byerly（1849—1935)的《傅里叶级数与球谐函数》(Fouries Series and Spherical Harmonics)[10]，这说明三角级数已经成为当时北京大学数学系本科生课程（属于选修课程）。

在浙江大学1929、1930 两年度数学系课程表[11]中，已有级数概论、实函数论等课程，其中，实函数论课程曾以英国数学家E. W. Hobson（1856—l933) 的《实变函数论与傅里叶级数论》(The Theory of Function of a Real Variable and the Theory of Fourier Series)等为主要参考书。由此可见，浙江大学的本科教学内容也包含了丰富的傅里叶级数理论。

2.2 研究生教育

我国傅里叶级数的研究生教育主要集中在浙江大学。1940 年2 月，西迁遵义的浙江大学数学系终于在湄潭等地暂时安定下来，有了一个相对稳定的环境。陈建功与苏步青协商，创办浙江大学数学研究所，招收数学研究生。从此，浙江大学数学系跨上了新的台阶。

1940—1946 年，浙江大学在函数论方向共培养了3 位硕士，分别是：

程民德，他是陈建功招收的第一名研究生，研究方向为傅里叶分析，1943 年毕业，硕士论文题目为《三角级数之研究》；

魏德馨，1945 年毕业，硕士论文题目为《线性运算与级数求和法》；

项黼宸，1946 年毕业；硕士论文题目为《傅里叶级数(C.-⊥＜a＜⊥)之求和》。

2.3 研究讨论班教育

我国大学授课的研究讨论班形式始于浙江大学。自1931 年起，在陈建功与苏步青的领导下，浙江大学数学系开始举办数学讨论班[12]，“吸收高年级学生和青年助教参加，并将讨论班定名为‘数学研究’”[13]。

陈建功、苏步青创立的讨论班研究性教学方法取得了巨大成功。在函数论讨论班中，傅里叶分析是主要讨论内容之一。陈建功指导当时的四年级在读本科生叶彦谦就Paley 与Wiener 关于傅里叶变换的文献在讨论班上做报告[14]，之后，又指导他研读傅里叶级数方面的论文，希望他开展相关研究工作。从现有资料看，王福春、卢庆骏、徐瑞云、程民德、叶彦谦、冯乃谦、朱良璧、项黼宸、魏德馨等都曾是讨论班的学员，而且，都取得了较好的科研成果。

3 我国傅里叶级数学者的学术谱系

关于我国傅里叶分析领域学者的师承关系，按照10 年为一代进行学术谱系划分。

第一代傅里叶分析学者主要是陈建功，他的导师为日本著名数学家藤原松三郎。陈建功培养了我国第二代傅里叶分析专家王福春。

第二代傅里叶分析学者主要有王福春、周鸿经、周怀衡等。王福春曾是陈建功的学生，后来在日本留学，导师也是藤原松三郎；项黼宸、程民德、魏德馨、叶彦谦等也是陈建功的学生。周鸿经毕业于原东南大学，熊庆来、何鲁、段子燮、周家树等曾是他的老师，后在英国伦敦大学留学，导师为L.S.Bosanquet。周怀衡曾在原东南大学、中央大学学习，熊庆来、何鲁、段子燮、周家树等曾是他的老师，后在英国剑桥大学留学，学习数学。

第三代傅里叶分析学者主要有冯乃谦、卢庆骏、徐瑞云、项黼宸、程民德、魏德馨、朱良璧等。这代学者或在本科或在研究生期间均曾受教于陈建功先生，而项黼宸、程民德、魏德馨等曾受教于王福春先生。卢庆骏的博士生导师为世界著名三角级数大师A. Zygmund；徐瑞云的博士生导师为世界著名数学家C.Carthéodory；程民德的博士生导师为世界著名数学家S.Bochner。S·Bochner 是美国科学院院士，曾任美国数学会副主席，其著作《傅里叶积分讲义》引入了被广泛运用的博赫纳积分等研究多重傅里叶级数收敛问题及逼近论问题的重要工具。

我国傅里叶分析学者学术谱系如图1 所示。其中，虚线框内的为浙江大学函数论学派学者的学术谱系。

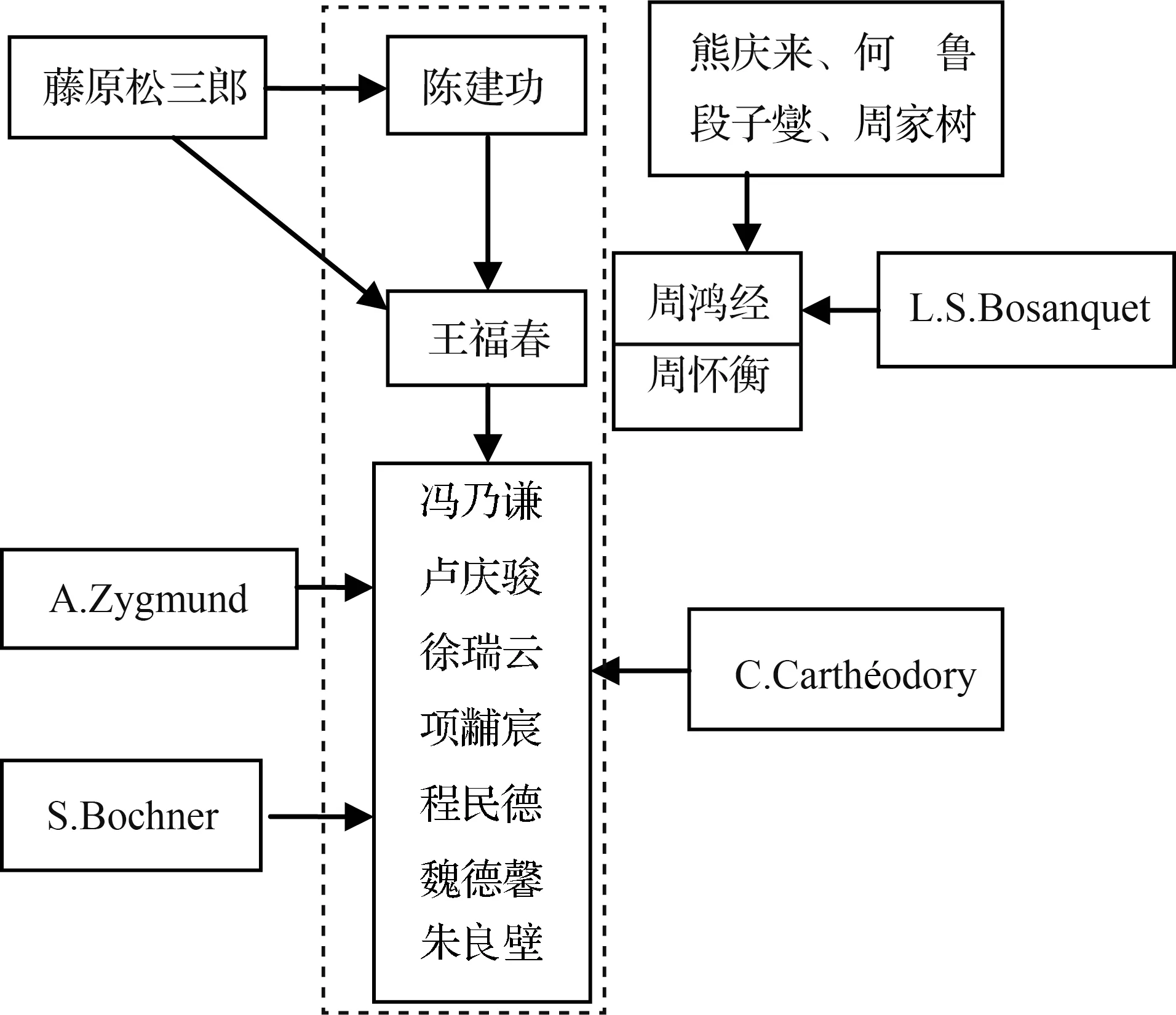
图1 我国傅里叶级数学者学术谱系Fig.1 The academic pedigree of scholar on Fourier series in China

4 浙江大学函数论学派的主要学术贡献

4.1 陈建功的主要贡献［15-16］

陈建功（1893—1971），浙江绍兴人。1913 年毕业于浙江两级师范学堂，同年考取官费留学日本资格，赴日本东京高等工业学校学习染色工艺；1919年回国，受聘于浙江省立甲种工业学校，教授染织工业课程。1920 年，陈建功二次东渡日本，入东北帝国大学数学系学习，次年在日本《东北数学杂志》上发表论文《关于无穷乘积的几个定理》。据现有资料[3-5]，在此之前，我国学者在国外发表的现代数学论文仅有王季同（1911）、胡明复（1918，博士学位论文）、赵元任（1919，1920）4 篇论文[5]。苏步青在《陈建功文集》（科学出版社，1981）序言中提到：“（这篇论文）无论是在时间上或是在内容上，都标志了中国现代数学的兴起，是具有重要意义的一篇创造性著作。从此以后，特别是从1927 年以后，我国数学家在国内外数学专刊上发表的论文不断增加。”

1923 年，陈建功毕业，受聘于浙江工业专门学校，教授数学，翌年被聘为国立武昌大学数学系教授。1926 年，他三渡日本，再次进入东北帝国大学数学系攻读博士学位，师从藤原松三郎，研究三角级数论。这是我国学者系统学习与研究傅里叶级数的始点。

收敛性是傅里叶级数中最为重要的问题。该理论的创始人Fourier 在19 世纪初期就认为，一切周期函数f(x)在满足一定条件下都是三角级数在点态收敛意义下的和。至1876 年，数学家Du Boise-Reymond 构造了一个周期为2π 的连续函数，在周期区间内除一点外为某三角级数之和，在此例外点上该三角级数不收敛，从而引起了对三角级数收敛性的讨论，包括三角级数在一点的收敛性与整体的绝对收敛性，并使得“函数的傅里叶级数是否必收敛于函数本身”成为三角级数研究的中心课题。

关于傅里叶级数整体绝对收敛的判别定理有Bernstain 判 别 法、Zygmund 判 别 法 等。1928 年，陈建功在《日本帝国科学院院刊》第4 卷上发表《论带有绝对收敛的傅氏级数的函数类》[1]，提出三角级数绝对收敛的刻画定理：

一个周期为2π 的三角级数绝对收敛的充分必要条件是该三角级数为Young 的连续函数的傅里叶级数。其中，Young 的连续函数是指周期为2π 的函数f(x)，且为2 个平方可积函数的卷积。

同年，英国数学家Hardy 和Littlewood 获得相同结果，他们的文章发表在《德国数学杂志》第28 卷上。由于《日本帝国科学院院刊》的国际知名度相对较小，因而人们称这一漂亮结果为“Hardy-Littlewood 定理”，事实上准确的命名应为“Chen-Hardy-Littlewood 定理”。如上所言，这是我国现代数学追赶世界先进水平的第一个标志性成果。

关于傅里叶级数在一点的收敛性的判别方法有多种，如由Dini、Jordan、Dirichlet、Gergen 等数学家建立的方法，但这些判别方法都仅给出了傅里叶级数在一点收敛的充分条件。1930 年，陈建功首先指出傅里叶级数在点x0处收敛的充分必要条件[11]：

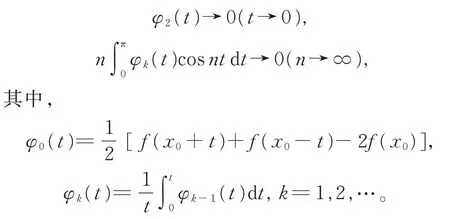
对傅里叶级数共轭级数收敛性的判定方法有Misra 判别法。1942 年，陈建功给出了一个新结果[18]，此结果相当于傅里叶级数收敛性的Gergen 判别法，是对Misra 判别法的改进。

1945 年，他进一步讨论了傅里叶级数与其共轭级数在点x0处的绝对收敛性：

20 世纪初，自Lebesgue 测度与积分理论问世后，一方面，将Riemann 积分推广至Lebesgue 积分、Denjoy 积分、Stieltjes 积分，将Cauchy 的连续定义推广至半连续、平均连续、全连续等；另一方面，Fejer将研究者对傅里叶级数收敛性的讨论引导至求和、强性收敛等方面，极大地丰富了傅里叶级数研究的内容和方法。

Cesàro 绝对可和性，即|C,α|可和性，是绝对收敛性的推广，其中|C,0|可和等价于绝对可收敛。设

那么，当α＞α0时，f(x)的傅里叶级数在点x0|C,α|可 和；当β＞-k时，f(x) 的 傅 里 叶 级 数 在 点x0|C,β|可和[21]。这一结果推广了Zygmund 关于傅里叶级数的绝对收敛定理。

1906 年，P. J. L. Fatou（法图）首先给出了一个傅里叶级数几乎处处收敛的条件，设

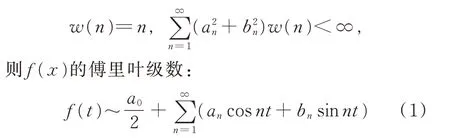
几乎处处收敛。1909 年，H.Weyl 将条件w(n)=n降为w(n)=；1913 年，E. W. Hobson 又将条件降为w(n)=nε,其中,ε＞0 为 任 意 正 数；同 年M.Plancherel 和G. H. Hard 又分别将条件改进为w(n)=log3n与w(n)=log2n。不久，N. Lsuin 进一步提出猜想（卢津猜想）：w(n)=1，即当式(1)为平方可积函数的傅里叶级数时，其几乎处处收敛。卢津猜想引起了世界上许多数学家的关注，如A. N.Kolmogoroff 等。围绕卢津猜想，在长达53 a 的研究中，出现了许多重要成果，如Kolmogoroff 与A.Plessner 进一步将条件w(n)=n降为w(n)=lgn。考虑到傅里叶级数式（1）是由殊特的就范直交函数系{1,sinnx,cosnx},n=1,2,…所组成，人们自然会问，卢津猜想对于一般就范直交函数系{φn(x)}所组成的傅里叶级数是否也成立? H.Rademacher（1922），D. E. Menchoff（1926），S. Bergen 与S.Kaczmarz（1927）分别给出了判别结果，随后，陈建功于1928 年 指 出，Rademacher,Menchoff，Bergen 与Kaczmant 的判别结果是等价的[22]，为卢津猜想的证明提供了新的思路。1966 年，瑞典数学家L.Carleson 证明了卢津猜想。

对于区间(a,b) 上的正交函数系{φn(x)}，定义：为 其Lebegue 函 数。1922 年，Rademacher 给 出 了lgn估计：

在区间(a,b)几乎处处成立。

Hilb 认为这一估计是最佳的。1929 年，陈建功对此估计做了改进[23]，得到

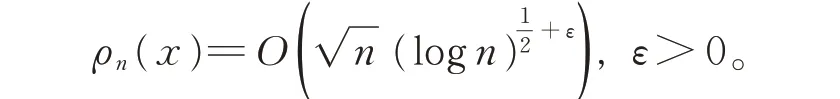
另外，1928—1950 年，陈建功还有6 篇关于单叶函数的论文在国外学术期刊上发表。

4.2 王福春的主要贡献［24］

王福春（1901—1947），字梦强，江西安福县人。1922—1927 年在武昌高等师范学校就学，是陈建功先生的学生。1929 年春起，王福春在日本东北帝国大学留学，师从藤原松三郎（亦是陈建功的导师）。研究方向为傅里叶级数与黎曼（Riemann）ζ 函数，研究工作主要集中在傅里叶级数强性求和（strong summability）、绝对求和(absolute summability)、里斯求和(Riesz summability)及求和因子等方面。

王福春的许多工作是基于Hardy 和Littlewood的傅里叶级数研究工作的，并进行了改进与深化。1933 年，王福春在《日本帝国科学院通报》上发表了第1 篇论文[25]，解决了G.H.Hardy 于1931 年提出的2 个问题并推广了A.Zygmund 用里斯对数平均求傅里叶级数和的定理。

关于傅里叶级数的里斯求和法，王福春讨论了(R,ewt,k)的求和法及其在收敛理论上的应用，主要结果如下[26-29]：

（i）若φ(t) 满 足φ(u)|du=o(t),t→0，则f(x)的傅里叶级数f(t)在t=x处(R,ewt,k)可和；若0 ＜α＜1 对 某 一k＞0 成 立，则f(t)必 在t=x处(R,ewt,h)可和，其中h为任意正数。

（ii）若φ(t)满足

则 对γ＞0，f(x) 的 傅 里 叶 级 数f(t) 在t=x处(R,ewt,γ)可和。

1934 年，Hardy 和Littlewood 在《傅里叶级数收敛的几个新准则》一书中证明了下述定理[30]：

设f(x)∈L2π是周期为2π 的勒贝格可积函数，若φ(t)满足式（2），且

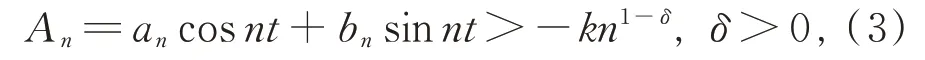
则f(x)的傅里叶级数f(t)在点x处收敛。

进一步，提出问题：定理中式（2）的条件能否减弱为

王福春证明了存在连续函数φ(t)，尽管φ(t)满足式（3）和式（4），但其傅里叶级数在t=0 处是发散的，从而对上述问题做出了否定回答。同时，进一步证明此问题可用(R,e(lgw)2,1+δ)平均法求和，且只需δ＞0。还证明了若将式（2）和式（3）分别改为

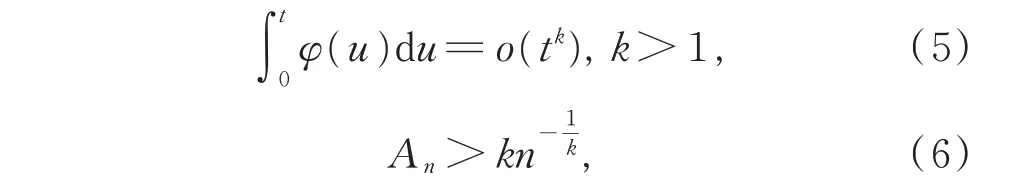
则Hardy-Littlewood 问题成立。同时指出，上述问题还可由下述条件推得：

在傅里叶级数强性求和法方面，王福春证明了Hardy 和Littlewood 于1935 年提出 的推测[31]：

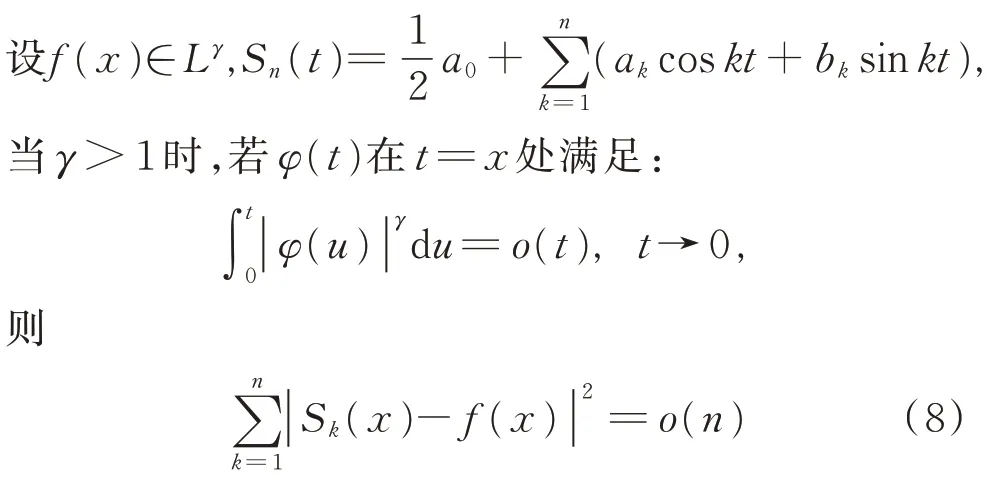
在该点成立。

Hardy 和Littlewood，Carleman 均证明了这一结果，但此结果在γ=1 时不成立。Hardy 和Littlewood 推测：若|f|lg+|f|可积，φ(t)在t=x处满足

则式（8）成立。

王福春证明了这一推测。进一步，他还证明，若将式（9）改为

则式（8）也成立[32-34]。

在傅里叶级数绝对求和法方面，王福春得到的主要结果如下[35-36]：

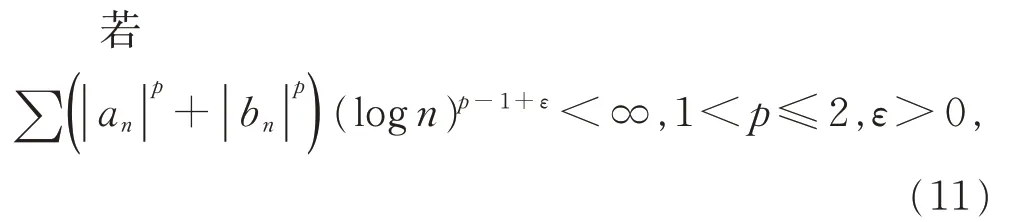
则f(x)的傅里叶级数f(t)几乎处处|C,α|可和。此时，ε≠0。当ε=0 时，f(t)虽 然 满 足 式（11），但f(x)的傅里叶级数f(t)在每个t=x处几乎都不能以|A|平均法求和。

王福春的另一项工作是关于黎曼ζ 函数的研究。民国时期，他在国外学术期刊上发表了6 篇关于黎曼ζ 函数的学术论文。改进了由Littlewood 得到的中值定理，并对黎曼ζ 函数的零点个数进行了估计；改进了由R. Paler 和N. Wiener 得到的中值定理，并获得一个可比肩普通中值定理的公式。

王福春一直拖病进行黎曼ζ 函数研究，直至去世。

王福春的这些工作得到中外数学界的一致好评。日本岩波书店于1983 年出版的《日本数学100年史》中，介绍了我国留学生陈建功、王福春和苏步青的工作：“其（王福春）成绩使日本治数学者惊异，吾国数学见重于日本，实以陈建功与先生及苏步青三君为始。”国际著名数学家Hardy 与Littlewood 对王福春亦赞赏有加：“俱于先生之成就，极力赞许”。正因为在傅里叶分析方面的卓越贡献，王福春2 次获得民国政府学术奖励。

由于长期超负荷工作，加之全面抗战爆发，当时的贵州省湄潭县物资匮乏，生活困苦、营养缺乏，王福春患上较严重的肺病。全面抗战胜利后，1946 年7 月，浙江大学回迁杭州，王福春因病重只能暂留湄潭，待病情稍有好转，于1946 年11 月接受中正大学之聘，任新成立的中正大学数学系第一任系主任。在中正大学期间，他一方面主持数学系工作，坚持为学生上课，另一方面仍致力于黎曼ζ 函数研究，终因劳累过度，导致肺病加剧，于1947 年9 月26 日病逝于南昌，享年46 岁。

4.3 卢庆骏的主要贡献

卢庆骏(1913—1995)，江苏镇江人。1936 年8 月毕业于浙江大学数学系，后留校任教。1946 年9 月被选派至美国芝加哥大学数学研究院学习，师从国际著名三角级数大师A.Zygmund，1948 年获博士学位，1949 年回国并被聘为浙江大学数学系教授，兼任数学系主任。

从1941 年至1950 年，在陈建功先生的指导下，卢庆骏主要从事傅里叶级数分析研究，先后发表11篇有关傅里叶级数的研究论文。其中最有名的工作是与王福春、程民德等一起共同解决了著名数学家G.H.Hardy，J.E.Littewood 和Z.Zalewaser 等提出的一个悬而未决的问题：

设{Sn(k)}为可积函数f(x)的傅里叶级数的部分和数列，{Sn(k(x))}是否几乎处处可用α＞0 阶Cesáro 求和？

王福春解决了k=2 的情形，程民德解决了k=2和3 的情形，卢庆骏利用Van der Corput 关于三角和的绝对值估计结果，完全解决了Z.Zalewaser 问 题[37]。

此后，卢庆骏在缺项傅里叶级数、傅里叶级数强性求和等方面获得了一系列结果，并在幂级数与傅里叶级数的绝对求和性方面得到了较深入的结果。1943 年，卢庆骏以《傅氏级数之求和论》（论文）获民国政府学术奖励三等奖。

4.4 徐瑞云的主要贡献［38］

徐瑞云（1915—1969），浙江慈溪人，是我国第一位数学女博士。1936 年，她以优异的成绩毕业于浙江大学数学系，后留校任教。1937 年10 月，进入德国慕尼黑明兴大学，师从著名数学家C.Carathéodory，研究三角级数论。

1940 年，徐瑞云获得博士学位，学位论文题目为《关于勒贝格分解中奇异函数的傅里叶展开》[39]，该文主要研究有界变差函数傅里叶级数的特征。1941 年，她返回浙江大学，被聘为副教授，继续研究有界变差函数傅里叶级数的特征，得到以下重要结果[40]：

设f(θ)是区间0 ≤θ≤2π 中的有界变差函数，其 变 差f(2π-0)-f(+0)=πσ( ＞0)，设 其 傅 里叶级数为

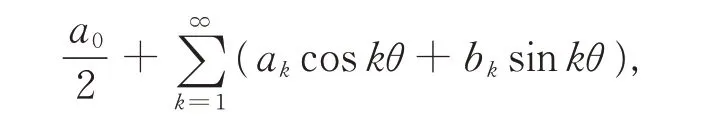
此时有勒贝格分解：

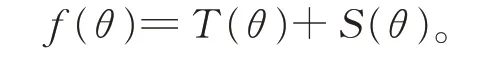
徐瑞云指出，对满足上述条件的所有函数f(θ)，在2n维空间中的点：

的变化范围是一个n阶Carathéodory 区域；进一步，如果前2n个傅里叶级数的系数ak,bk(1≤k≤n)保持不变，则在由此类函数构成的函数集中，S有正的最小值S*n，且S*n还可用此2n个傅里叶级数的系数表示。

4.5 程民德的主要贡献［41］

程民德（1917—1998），1935 年考入浙江大学电机系，后转入数学系学习；1940—1942 年，在浙江大学数学研究所攻读硕士学位，师从陈建功先生，研究方向为傅里叶分析理论；1943—1945 年，任浙江大学数学系讲师；1946—1947 年，任北京大学数学系讲师；1947 年，进入美国普林斯顿大学数学系，在著名数学家S.Bochner 教授指导下，进行多元调和分析研究，1949 年获得博士学位；后在著名数学家E.Artin 与C.Chevalley 指导下做博士后研究，1950 年1月回国。

程民德的早期工作是研究一元傅里叶级数各种求和法以及求和因子等，共发表学术论文21 篇。如前所述，他的第1 篇论文是与王福春、卢庆骏一起解决 了Hardy，Littlewood 和Z.Zalewaser 等 提 出 的 问题[42]。第2 篇论文得到了三角级数在整个区间上收敛的充分必要条件[43]。此后一段时间，他的主要工作集中在傅里叶级数的Cesáro 可求和性、傅里叶级数的可求和性因子、Bochner-Riese 平均的Gibbs 现象等方面。在文献[44]中，他证明了以下结果：

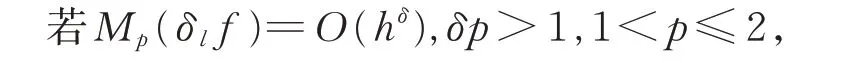
则[φ(t)]1在(0,π)是有界变差的，且[φ(t)]1的傅里叶级数绝对收敛。

在文献[45]中，他得到了傅里叶级数在点x处的可求和性条件。

程民德的另一主要贡献是在调和分析方面。调和分析也称傅里叶分析，来源于傅里叶级数，形成于18 世纪。但由于多种原因，20 世纪40 年代前，多元调和分析一直未能取得实质性突破。程民德在S.Bochner 指导下，将研究方向从一元转向多元，很快在多重三角级数唯一性上取得了成果[46]。调和函数是满足拉普拉斯方程Δu=0 的二次连续可微函数，而m重调和函数是满足方程Δm u=0 的2m次连续可微函数。但当函数u仅有较少的光滑性时，如仅知u有2m-2 次连续可微时，如何刻画u的m重调和 性？1916 年，W.J.E.Blaschke 解 决 了m=1 的 情形；20 世纪30 年代，D.Nicolesco 对 一般的m做了类似的刻画。程民德证明了：如果二重（或多重）三角级数的圆形和按|C,1|可求和到零，则其系数皆为零。为证明多重三角级数的唯一性定理，他将研究领域拓展至多重调和级数，并发现D. Nicolesco 对一般的m做的有关函数u的m重调和性，给出的仅为必要而非充分条件。为此，他引进了广义多重拉普拉斯运算概念（记为∇m），并且在函数u是2m-2次连续可微条件下证明了Δm u=0 的充分必要条件是∇m u=0。这一结果堪称经典。

限于篇幅，有关项黼宸、朱良璧、魏德馨等的工作不再赘述。

5 总 结

陈建功是我国傅里叶级数研究的开创者、领导者。浙江大学函数论学派是傅里叶级数在我国的主要研究、教育、传播、发展基地。陈建功培养了王福春、卢庆骏、徐瑞云、项黼宸、程民德、魏德馨等我国第二代、第三代傅里叶级数学者。王福春、周鸿经等我国第二代傅里叶级数学者，对于推动傅里叶级数在我国的传播、研究和发展起了积极作用。徐瑞云、程民德等是我国第三代傅里叶级数学者，对于傅里叶级数在我国的进一步发展起了承前启后的作用。项黼宸、程民德、魏德馨是1949 年前我国培养的傅里叶级数方向的硕士。傅里叶级数研究是我国现代数学研究的先驱与领头羊，对于推动现代数学在我国的传播、发展起了带头和引领作用。