单罐储热系统的动态特性数值研究

曹瑞峰，赵 浩，高 建

(东北电力大学能源与动力工程学院，吉林 吉林 132012)

能源结构比例的不合理产生了新能源和传统能源之间的协调问题.为了满足调峰的需求，电网不得不承受大量弃光弃风现象的出现，致使新能源发电能力无法得到有效的利用.储热技术被认为是解决这一困境的关键性技术，通过加设储热系统，将多余的能量以热能的形式储存起来，可以有效提高新能源的利用效率[1].同时，太阳能自身稳定性差，需要利用储热系统才能使太阳能发电长时间的稳定运行[2].目前，双罐显热储热系统的技术已经完全成熟，但是双罐储热系统的结构复杂、成本较高.单罐储热系统只有一个储热罐，罐内的冷热流体之间会因为密度差的存在而自然形成一个具有很大温度梯度但很薄的斜温层，冷热流体通过斜温层隔开储存.单罐储热系统的成本要比双罐系统低很多，同时还可通过在储热罐内填充低成本的固体颗粒填充物来进一步降低成本.因此，斜温层单罐储热技术近年来得到了越来越多研究.

仿真方面，许昌等[3]建立了容积式吸热器的稳态传热模型，计算出了太阳能多孔介质结构吸热器的容积换热系数，并与实验数据进行比较，证明了模型的可靠性.柳文洁[4]建立了热水储热罐模型，模拟计算发现储热罐的形状，布水器开口的流速，布水器进口、出口的水温温差等因素对热水储热罐的热特性有较大影响.程友良等[5]对熔盐在储热单罐中的流动规律和传热特性进行数值模拟研究.研究结果表明：随着熔盐入口流速的增大，斜温层厚度逐渐增加，储热效率会逐渐降低，但过低的入口流速会延长储热周期.实验方面，孙晓丽等[6]从储热单罐内熔盐温度分布、放热换热器出口温度、放热换热量、放热换热器的效率对单罐储热系统的放热过程进行实验研究.崔武军[7]研究了熔盐储热罐内的温度分布变化与散热规律，通过对罐体进行加热、内循环及冷却等实验，得到了罐体在运行状态下的温度分布数据，并分析拟合得到了在自然冷却过程中熔盐罐的散热功率随时间和温度的变化曲线.

目前大多数的研究工作集中在斜温层储热罐中的流动特性、传热特性以及热力学特性等方面，但对于斜温层储热罐动态特性的研究涉及不多.储热罐作为热量转换系统中的一部分，总是要和其他用能设备(如涡轮、热网换热器等)连接.储热罐能否快速的响应用能设备的动态，对储热系统的运行至关重要.基于此，本文对斜温层储热单罐的动态特性进行了数值模拟研究，分析了关键参数对系统动态特性的影响规律.本文的研究结果可以为单罐储热系统的实际运行提供一定的指导作用.

1 数值模拟方法及其验证

1.1 数值模型

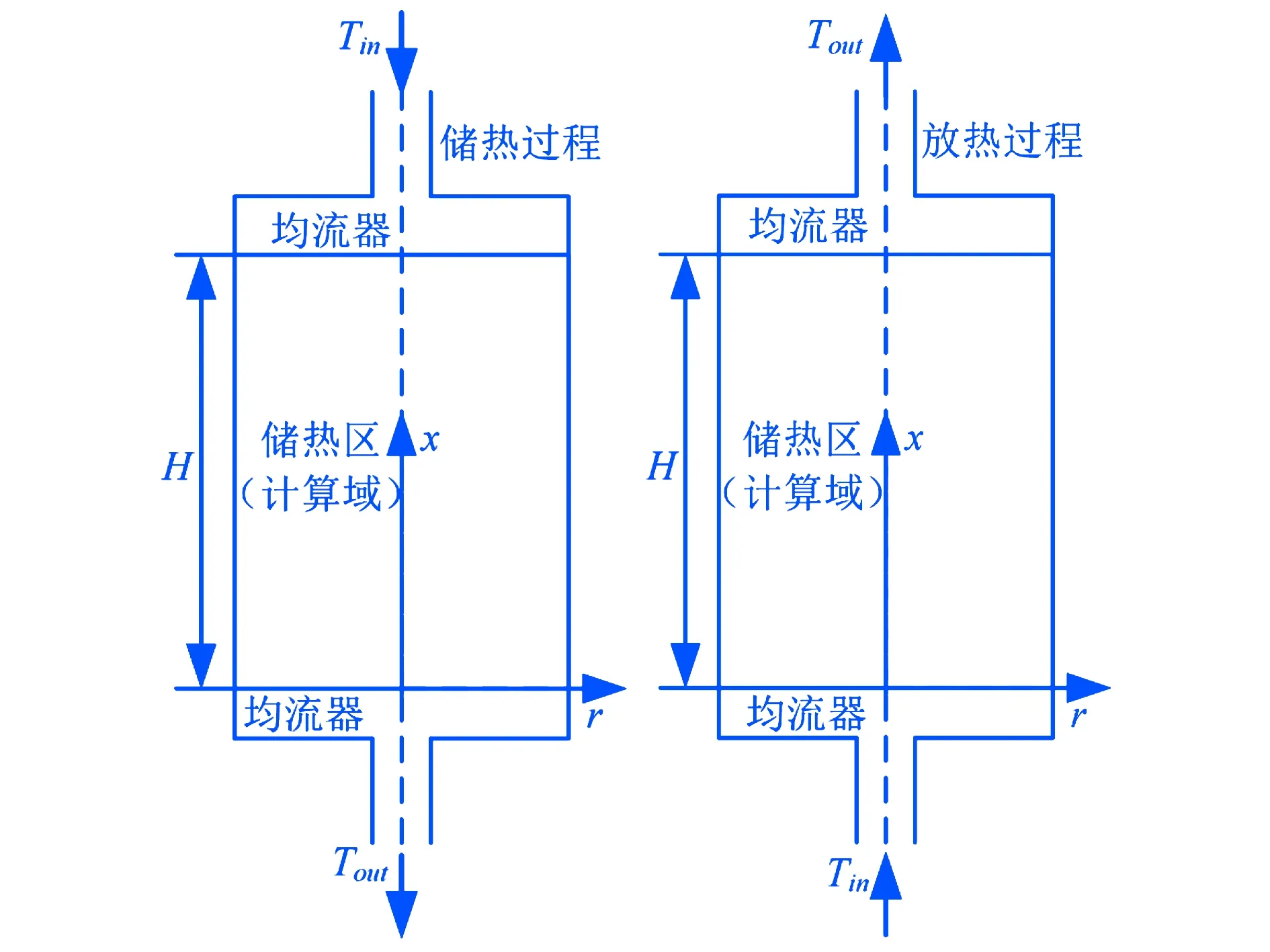
图1 斜温层储热单罐的结构简图与计算域

斜温层储热单罐的结构，如图1所示.单罐储热系统利用不同温度下储热介质的密度不同，实现冷热流体的自然分层.储热罐内顶部和底部通常具有较为复杂的结构(均流器)来保证产生较好的分层.

为简化分析对储热罐进行如下假设：

(1)忽略均流器复杂结构，认为罐内是一个均匀的流动过程；

(2)认为储热罐内为二维对称、非定常的管内层流；

(3)罐内流体为不可压缩流体；

(4)不考虑流体内部的粘性耗散效应；

(5)罐体对外绝热.

连续方程

(1)

动量方程

(2)

(3)

能量方程

(4)

公式中：ρ为熔融盐密度，kg/m3；u为熔融盐流度，m/s；μ为熔融盐动力粘度，Pa·s；T为熔融盐温度，K；t为蓄热罐蓄热时间，s；r为蓄热罐半径，m；v为熔融盐运动粘度，m2/s；λ为熔融盐有效导热系数，W/(m·K)；Fx为沿蓄热罐竖直方向的轴向力，N；Fr为沿蓄热罐水平方向的径向力，N.

本文采用Fluent软件，使用压力基隐式求解器进行求解N-S方程，求解过程采用二维双精度；考虑重力的影响，并采用 Boussinesq模型来解决浮力驱动问题；速度与压力之间的耦合采用 SIMPLE算法.边界条件和初始条件如下：

(1)罐体高度为H，直径为D，且罐体形状属于细长型(D<0.5L)；

(2)罐体外壁(r=D/2)做绝热处理，且忽略罐壁厚度；

(3)对于储热过程，计算域的上部进口温度为TH，下部进口流速为uin，下部出口温度为TL，下部出口流速为自由边界；

(4)对于放热过程，计算域的下部进口温度为TL，下部进口流速为uin，上部出口温度为TH，上部出口流速为自由边界；

(5)选用三元熔融盐(44% KNO3+7% NaNO3+49% NaNO2)作为储热介质，其密度ρ(kg·m-3)、导热系数k(W·m-1K-1)、比热Cp(J·kg-1K-1)以及粘度μ(kg·m-1s-1)随温度T(℃)的变化经验公式如下[8]：

ρ=2293.6-0.7497×T，

(5)

Cp=5 806-10.833×T+7.2413×10-3×T，

(6)

k=0.413 7+10.833×10-3×T，

(7)

μ=0.473 7-2.797×10-3T.

(8)

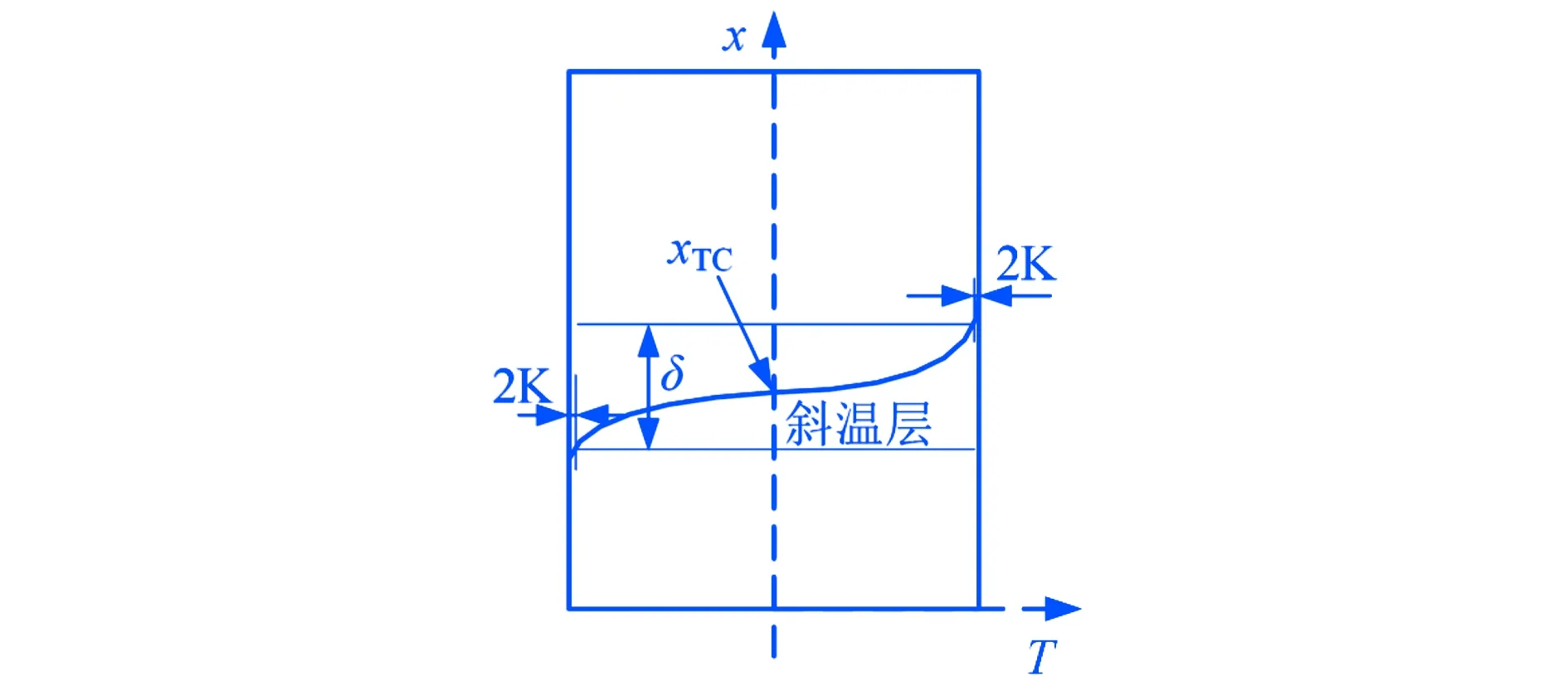
图2 斜温层厚度及其位置定义的示意图

斜温层厚度是评价斜温层储热单罐分层效率的一个常用指标.储热罐内的温度分布曲线是一条渐进曲线，如图2所示.因此,在确定斜温层厚度时通常把顶部和底部一部分忽略掉.本文选取比最高温度低2 K作为斜温层的上界限温度，比最低温度高2 K作为斜温层的下界限温度，上、下界限温度所对应的位置差定义为斜温层厚度δ.斜温层位置的变化反映了斜温层运动的情况，本文选取斜温层上、下界限温度所对应位置的中间值定义为斜温层位置.

1.2 网格无关性和步长独立性验证

本文选取储热过程中第11s时的斜温层厚度来进行网格无关性和步长独立性验证.验证所采用的模拟条件为一个储热过程，H=0.420 m，D=0.105 m，TL=523 K，TH=593 K，uin=0.03 m/s.

网格无关性验证的结果，如图3(a)所示.从图3(a)中可以看出，随着网格数的增加，斜温层厚度逐渐变小.从8万增大到16万时，斜温层厚度变化很小，可认为16万的网格已达到网格无关.因此本文选取16万做为计算网格数量.

步长独立性验证的结果，如图3(b)所示.从图3(b)中可以看出，随着时间步长的减小，斜温层厚度逐渐变小.当从0.001 s减小到0.000 1 s时，斜温层厚度的变化很小，因此本文选取0.001 s做为计算时间步长.

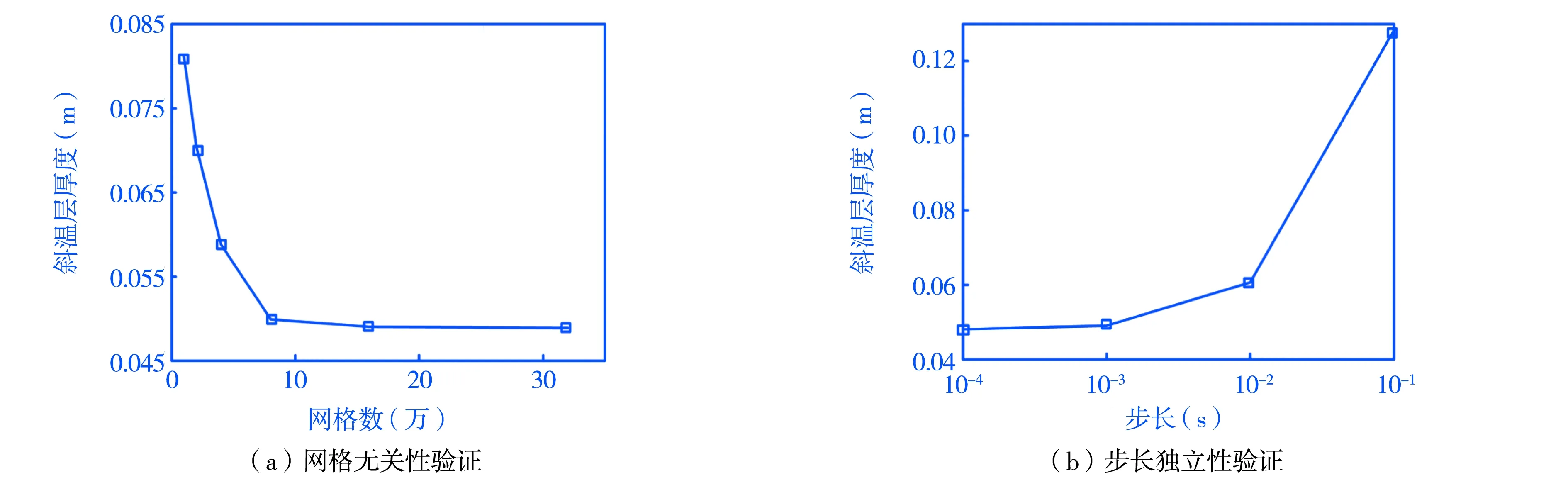
图3 网格无关性和步长独立性验证

1.3 数值模拟与实验结果的对比验证

储热过程中储热罐的中心轴线处的温度分布的模拟和实验[9]对比结果，如图4所示.从图4可以看出，实验结果曲线有一定的分散性，而数值模拟结果则呈现出明显的规律性，实验值的最高温度值略低于实验值.在不同时刻，数值模拟结果与实验结果曲线具有相同的温度点和位置点.虽然在高度方向上，实验测得的温度变化范围大于模拟结果，但是两者温度变化趋势基本一致，说明本文所建立的单罐储热数值模型的正确性以及数值模拟方法的可靠性.

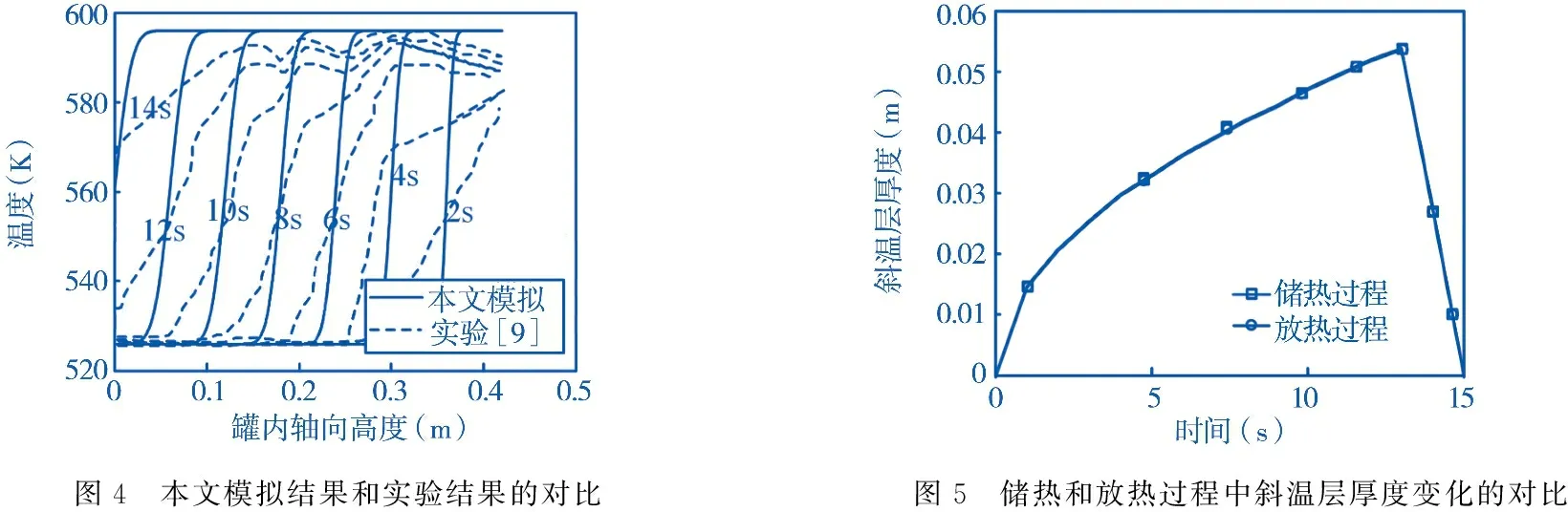
图4 本文模拟结果和实验结果的对比图5 储热和放热过程中斜温层厚度变化的对比

2 结果及分析

2.1 储、放热过程的对比

储热和放热过程中斜温层厚度随时间变化的对比情况，如图5所示.在储热过程和放热过程中，模拟条件为H=0.420 m，D=0.105 m，TL=523 K，TH=593 K，uin=0.03 m/s.从图5可以看出，在相同的进口速度下，储热过程和放热过程中斜温层厚度的变化趋势基本是一致的，放热过程可以看作是储热过程的逆过程.因此，在本文下面的分析中只针对储热过程进行分析，分析结果对于放热过程同样适用.

2.2 斜温层迁移特性影响因素分析

斜温层迁移特性是指储热罐内斜温层的运动特点，主要包括斜温层厚度的变化和斜温层运动速度的变化，其受进口速度、储热罐高径比、冷热储热流体温差等因素的影响.

2.2.1 不同进口速度的影响

为了分析不同进口速度对斜温层迁移特性的影响，本文选取了七种不同的进口速度进行了储热过程的模拟，其他条件为H=0.420 m，D=0.105 m，TL=523 K，TH=593 K，uin=0.03 m/s.

不同进口速度下斜温层厚度随时间的变化.随着储热过程的进行，如图6所示.斜温层逐渐增厚并在达到最大值后开始变薄，这是因为斜温层到达了储热罐底部并逐渐离开储热罐.进口速度越大，储热过程需要的时间越短，但在同一时刻下斜温层厚度越厚，这是因为较大的进口速度带来了更为严重的冷热流体掺混，形成了更厚的斜温层.不同进口速度下斜温层位置随时间的变化，如图7所示.从图7可以看出，进口速度越大，斜温层在罐内的运动速度越快，且斜温层位置与时间呈线性关系.分析发现，由于储热工质为不可压缩流体，斜温层的运动速度基本等于高温流体进口速度.

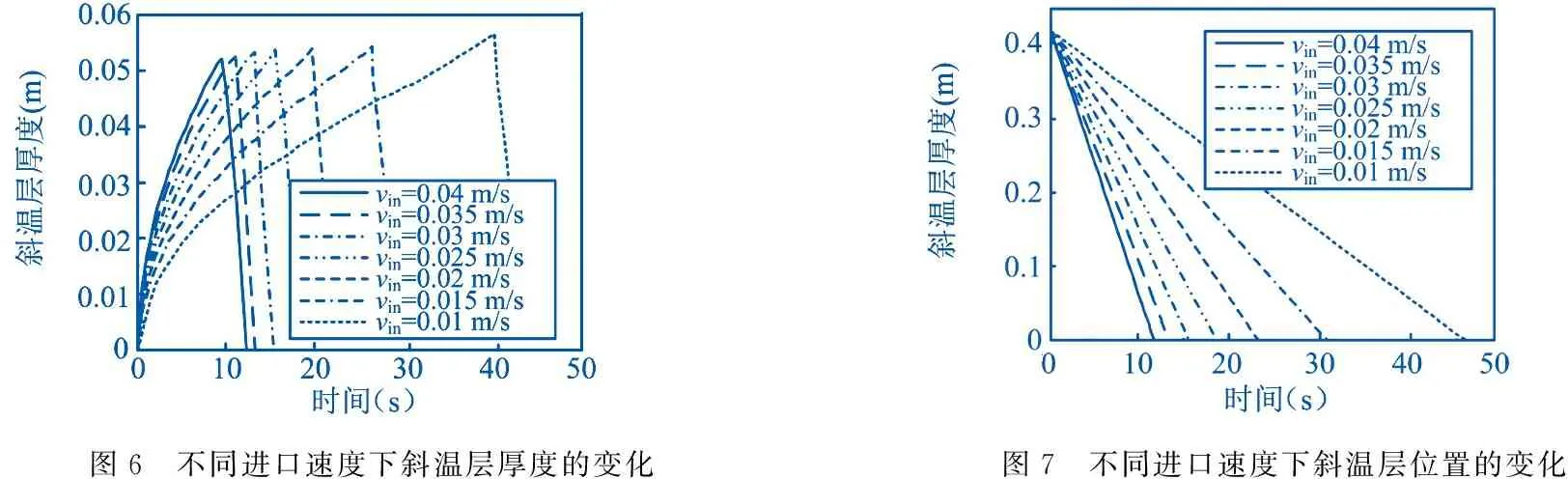
图6 不同进口速度下斜温层厚度的变化图7 不同进口速度下斜温层位置的变化

2.2.2 不同高径比的影响

为了分析不同高径比对斜温层迁移特性的影响，本文在固定储热罐直径的情况下，选取了三种不同的储热罐高度(高径比分别为4∶1、3∶1、2∶1)进行了储热过程的模拟，其他条件为D=0.105 m，TL=523 K，TH=593 K，uin=0.01 m/s.

不同高径比下斜温层厚度随时间的变化，如图8所示.在相同直径下，储热罐越矮，储热需要的时间最短，但在同一时刻下，斜温层厚度相同.不同高径比下斜温层位置随时间的变化，如图9所示.可以看出在不同高径比下，斜温层位置随时间的变化成线性关系，且斜温层的运动速度基本等于高温流体进口速度.综上，只要储热罐的直径相同，储热罐的高度变化并不会影响斜温层的迁移特性.但随着高度增大，储满时斜温层厚度越厚，由于斜温层厚度的增厚趋势趋于平缓，储热罐的储热效率有所提高.

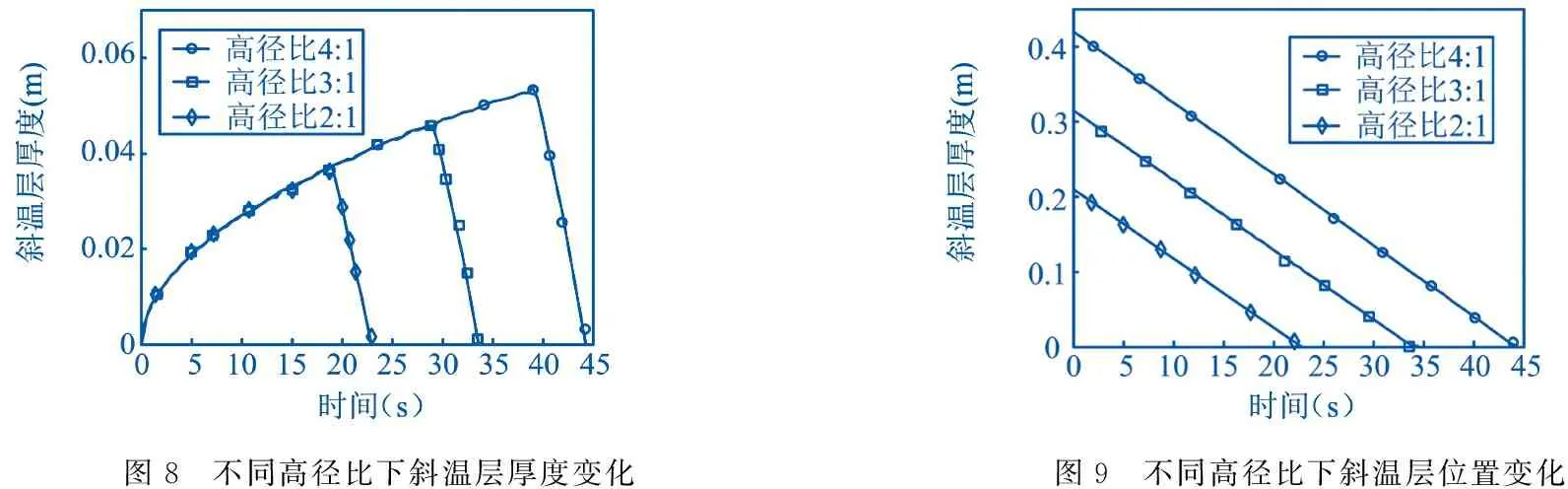
图8 不同高径比下斜温层厚度变化图9 不同高径比下斜温层位置变化

2.2.3 不同温差的影响

为了分析冷热流体温差对斜温层迁移特性的影响，本文在固定进口温度的条件下，选取了四种不同的低温储热流体温度(TL分别为523 K、503 K、483 K、463 K)进行了储热过程的模拟.其他条件为H=0.420 m，D=0.105 m，TH=593 K，uin=0.03 m/s.

不同温差下斜温层厚度随时间的变化，如图10所示.可以看出当冷热流体温差越大，同一时刻下斜温层厚度会越厚.这是由于冷热流体温差的增大导致两者之间的传热和传质效果增强造成的.不同温差下斜温层位置随时间的变化，如图11所示.可以看出斜温层的运动速度不受冷热流体温差的影响，而只取决于高温流体的进口速度.

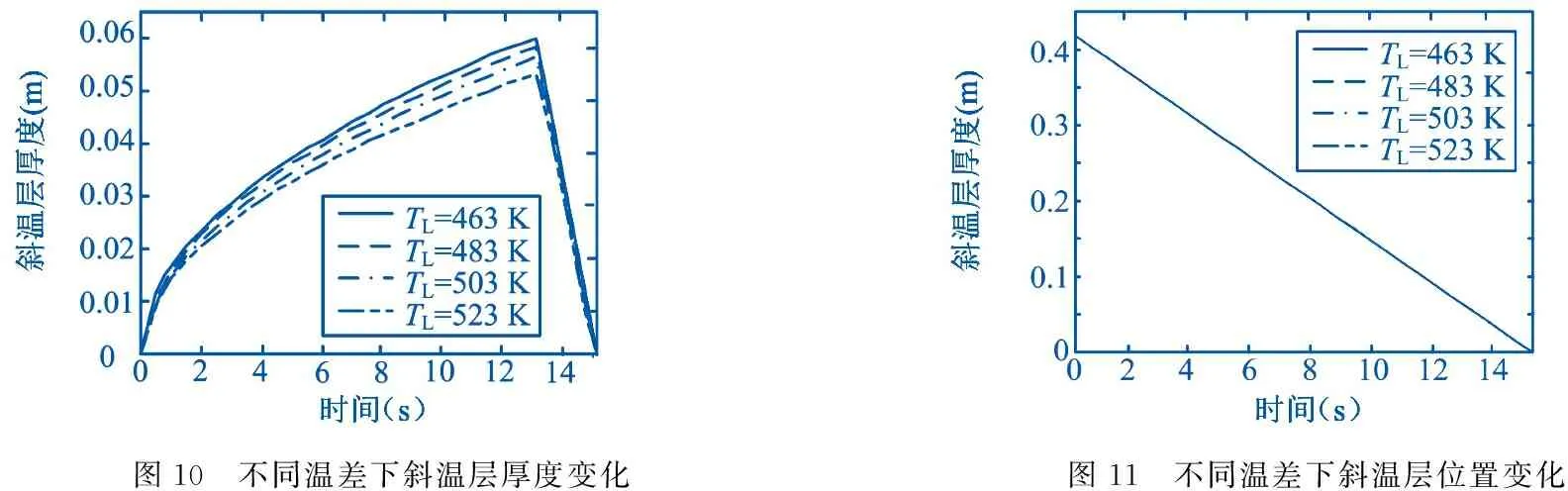
图10 不同温差下斜温层厚度变化图11 不同温差下斜温层位置变化

2.3 储热系统动态响应特性分析

本文通过阶跃响应法对储热系统的动态响应特性进行辨识.通过分析发现，储热系统出口速度对进口速度的响应特性近似于惯性环节,如图12所示.因此,假定储热系统动态响应传递函数为惯性环节，即有

(9)

公式中：T为动态响应时间常数，s；K为系统增益.

为方便进行模型辨识，对系统出口速度进行归一化，得到无量纲速度为

(10)

公式中：uout，min为阶跃前出口速度；uout，max为阶跃后达到稳定时的出口速度.

在下面关于动态响应特性的模拟过程中，选取的模拟条件为H=0.420 m，D=0.105 m，TH=593 K，TL=523 K.

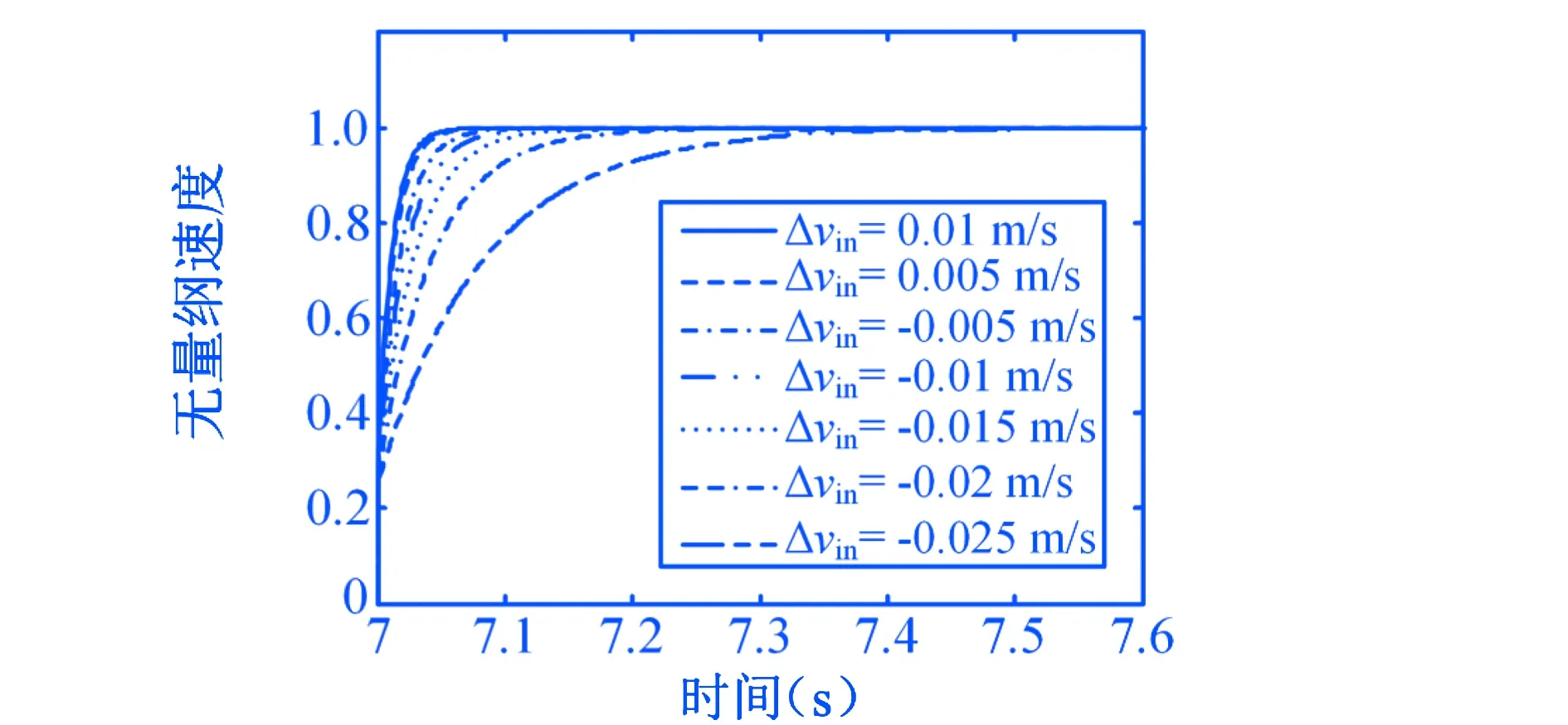
图12 不同进口速度阶跃量下系统动态响应曲线

2.3.1 不同速度阶跃量下的动态响应

为分析不同进口速度阶跃量下系统的动态特性，本文先以进口速度为0.03 m/s的条件进行储热，在第7秒时，突然改变进口速度，分析出口速度的变化情况,如图12所示.本文选择了7组不同的进口速度阶跃量进行了模拟.从图12可以看出，当进口速度正阶跃(突然增大)时，阶跃量越大，储热系统的响应越快；当进口速度负阶跃(突然减小)时，阶跃量越大，储热系统的响应越慢.通过模型辨识得到的系统时间常数和增益，如图13所示.从图13可知，在不同的进口速度阶跃量下，系统的响应速度相差接近一个数量级，但系统的增益几乎不变.

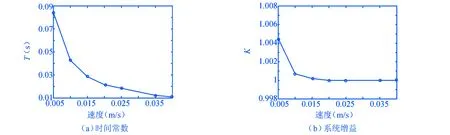
图13 在7 s处不同的速度响应

2.3.2 不同斜温层厚度下的动态响应

为了分析不同斜温层厚度对系统动态特性的影响，本文先以进口速度为0.03 m/s 的条件进行储热，然后在不同的时刻，突然改变进口速度为0.04 m/s，分析出口速度的变化情况.五个不同时刻发生进口速度阶跃时系统的动态响应过程，如图14所示.需要注意的是，为了对比分析的方便，此处对阶跃时间做了对齐处理.从图14可以看出，只要储热罐内形成了斜温层，系统的动态响应特性与斜温层厚度几乎没有关系.

图14 不同斜温层厚度下系统动态响应曲线图15 有无斜温层时系统动态响应曲线

2.3.3 有无斜温层时的动态响应

为了进一步分析斜温层的存在对系统动态响应特性的影响，本文设计了一个不存在斜温层的对比算例.该算例中进入储热罐的流体温度和储热罐内的冷流体温度相同，都为523 K，此时由于不存在温度差，罐内不会产生斜温层，而正常的储热罐仍设置进口温度为593 K.两个系统都以0.03 m/s 的进口速度运行到7 s时，突然改变进口速度，观察出口速度的变化情况.进口速度阶跃到0.04 m/s时，有无斜温层两个系统的动态响应的对比，如图15所示.不同的进口速度阶跃量下，有无斜温层两个系统的时间常数和增益(图上横坐标为不同的阶跃后速度)的对比，如图16所示.从图上可以看出，在任何阶跃量下，当储热罐内存在斜温层时，系统的响应速度要比无斜温层时快.但不管是否存在斜温层，单罐储热系统的增益相差不大，都接近于1.

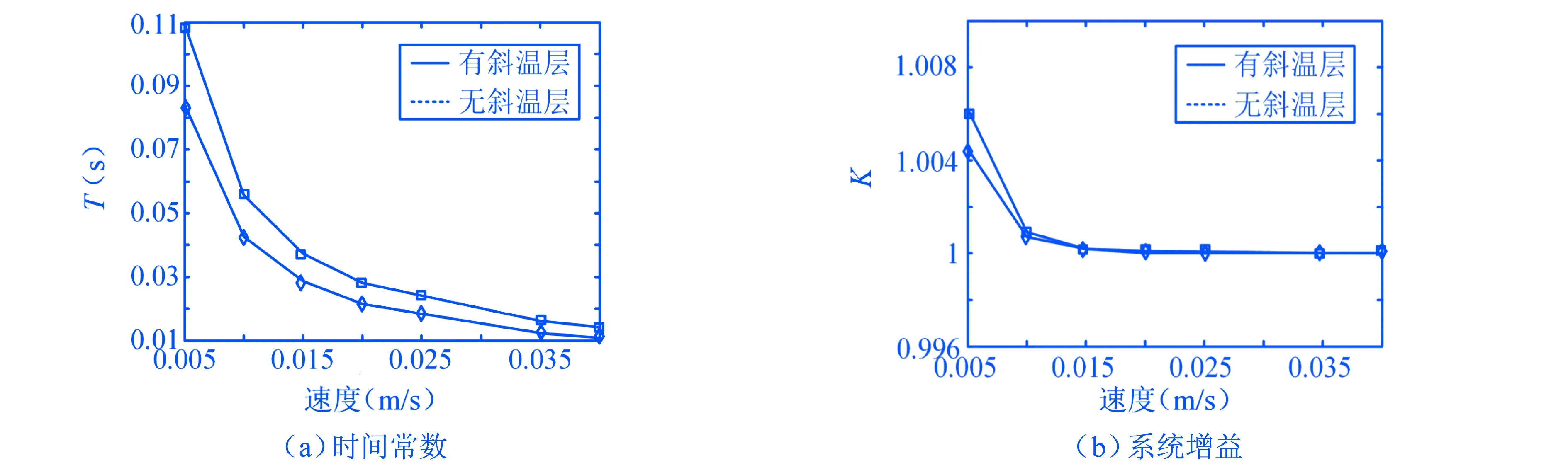
图16 有无斜温层时系统的动态响应特性对比

3 结 论

本文利用Fluent软件对三元熔盐在斜温层储热单罐内的流动规律和动态特性进行了数值模拟，分析了储热罐关键参数对斜温层厚度、斜温层位置以及系统动态响应特性的影响规律.得出了以下结论：

(1)储热过程和放热过程的斜温层运动特征基本一致.

(2)斜温层的运动速度基本等于进口流速.

(3)进口速度越小，同一时刻斜温层越薄，但储热时间越长；储热流体温差越大，斜温层越厚；斜温层迁移特性与储热罐的高度无关.

(4)进口速度正阶跃量越大，储热系统的响应越快；进口速度负阶跃量越大，储热系统的响应越慢.

(5)斜温层的厚度与罐内储热温差、入口速度等因素有关，与罐的高径比无关.

(6)在任何阶跃量下，当储热罐内存在斜温层时，系统的响应速度要比无斜温层时快，而不同的斜温层厚度对动态响应的影响不大.