基于区段定位的配电网混合线路故障行波测距新方法

王义军，曹 越，窦鹏志，曹凤建

(东北电力大学电气工程学院，吉林 吉林 132012)

配电系统是电网中最能体现供电可靠性的一环，配电网线路长度较短、分支较多、拓扑结构复杂，且多为电缆—架空线式混合线路[1]，相比于输电线路，配电线路中行波折反射的情况更加复杂.传统的行波测距方法在输电线路中多有应用，定位较为准确，但在配电网中应用时需要加以改进[2].

行波法因受系统参数、接地方式、故障点过渡电阻、线路负荷等影响小的优势得到良好发展[3].目前行波法中研究较多的是单端测距、双端测距和S注入法.文献[4-5]提出用单端行波法进行故障测距，原理简单且所需测量信息少、经济性好，但不适用于情况复杂的有源配电网中；文献[6-7]提出用线模分量和零模分量的时间差来测距，由于零模分量在线路传输过程中衰减严重，零模波速不易获取，会造成较大的误差；文献[8]结合双端非同步信息推导出一种修正行波波速的计算方法，通过优化波速带来的误差提高了测距精度.配电网在实际运行过程中，混合输电线路的架空线段发生故障的概率远大于电缆段，其中发生最多的故障是单相接地故障[9-10].故障发生后，正确判别故障区段以及精准故障定位，可以提高重合闸成功率、提高巡线效率和降低巡线难度，保证供电可靠性以及减少停电造成的损失[11-12].

本文以现有区段定位为基础，定义一种新的线路划分方法-1/2n区段法.即将配电网中每条线路均分为2n段，故障前根据线路已知信息可以求得每个区段节点发生故障时行波波头传递到两侧的理论时间差，建立信息基准量，将其与故障后线路两侧接收的实际行波波头时间差作对比，确定故障点所在线路区段.再由双端测距法定位故障点，配合故障区段搜索真实故障点.本方法不用对线路结构进行归一化处理，消除了因线路长度导致的测距误差和混合线路波速不同造成的时间误差，且n在合适范围内取值越大，故障线路划分的区段长度越小，有效提高了巡线效率和供电可靠性.

1 行波法应用分析

1.1 配电网故障点定位与区段定位

在输电网中，现有研究多运用单端和双端行波法对故障点进行直接定位，但是在配电网遇到特殊接线情况时，双端法会造成误判.简单配电网络M端和N端装有行波测量装置，如图1所示.以B1P1为中线，系统两侧对称，那么F1点与F2点发生故障时，由双端行波法得到的测距结果是相同的，所以双端法不完全满足配电网行波定位的要求，需在分支线路加装行波测量装置，且对装置布点进行优化，减少成本，构成利用多端接收行波首波头信息定位故障区段和故障点的方法.

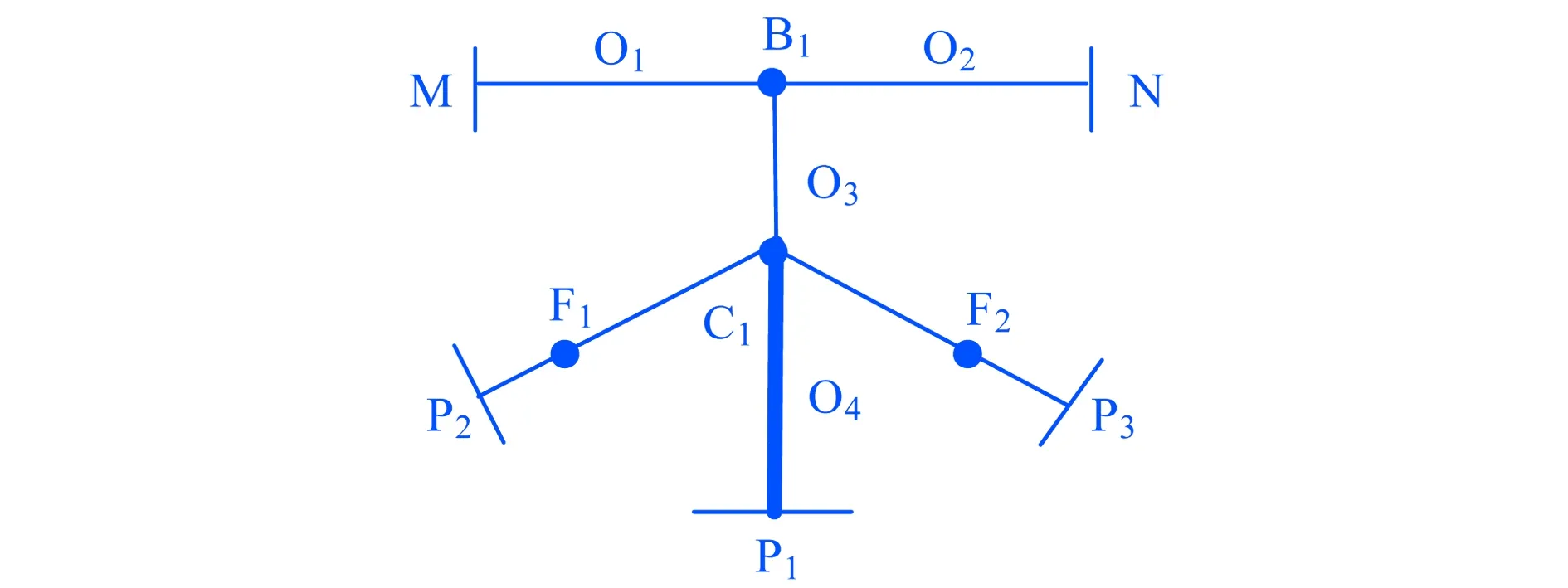
图1 简单配电网络

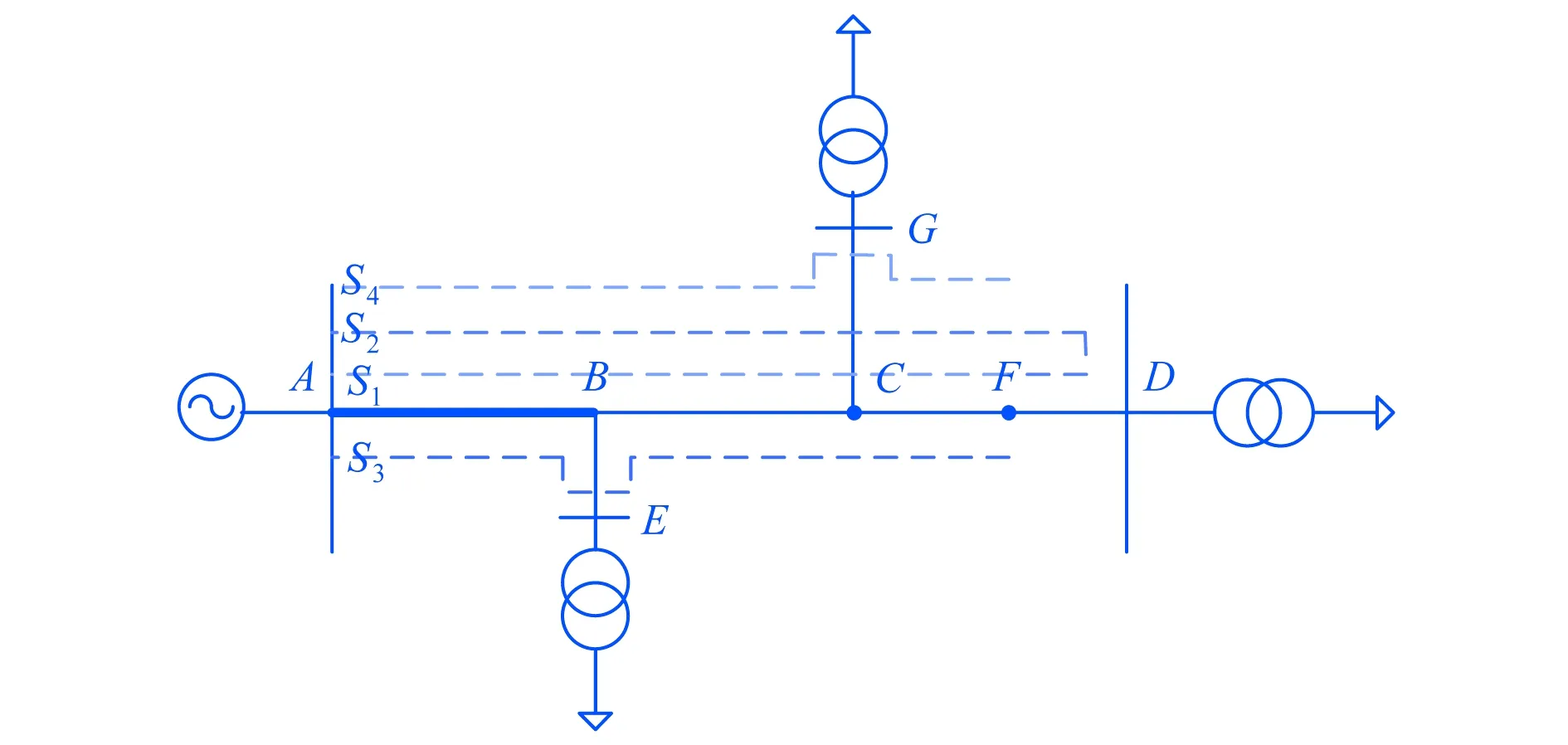
图2 行波传输路径

图3 均匀传输线路区段划分原理示意图

行波遇不同节点产生折反射后的传输路径，如图2所示.其中AB为电缆区段，BD为架空线区段，母线A处装有行波测量装置.

可以看出，行波在到达测量点的传输过程中具有唯一最短路径S1：F→C→B→A.若图1中的点F1发生故障，且在P1端和P2端加装测量装置，可由多端信息判断故障线路为C1P2并进一步判断故障区段.

现有研究中行波法的定位误差范围通常在50 m到500 m之间，若检修人员根据定位点向两侧搜索故障点，则搜索范围在100 m到1000 m之间，配电网因接线情况复杂，可能引起更大的误差，加大搜索范围，故提出1/2n区段法，先定位故障线路，并将故障线路等分为多个区段，进而搜寻故障区段定位故障点，缩小误差范围，提高定位精度.

2 混合线路故障区段确定

2.1 1/2n区段法定位原理

为配电网中一段长度和类型均已知的输电线路如图3所示.端点M、N设有行波测量装置，故障前对线路进行划分，将其平均分为2n个区段，每个区段长度相等，且有两个边界点.当n=1时，线路MN被分为MO1和O1N两个区段，边界点为M、O1、N；当n=2时，线路MN被分为MO2，O2O1，O1O3，O3N四个区段，边界点为M、O2、O1、O3、N.定义以上划分线路区段的边界点为区段节点.

由线路已知参数可求得行波传输速度

(1)

公式中：R、L、G、C分别为单位长度线路的电阻、电感、电导和电容；ω为角频率[13].

设线路全长为l，行波速度为Vj，可在系统正常运行状态下由线路已知参数计算第i个节点发生故障时，故障行波初始波头到达测量端点的理论时间差

(2)

故障后，由行波测距公式

(3)

可测得故障行波初始波头到达测量端点的真实时间差Δt和定位点x，Δt必然在[Δti，Δti+1]内，x对应距离在[li，li+1]内.

最后，由测量故障点向两边搜索，搜索范围在[0，li/i+1-lx]内.实际中的输电线路由多段、混合线路组成.

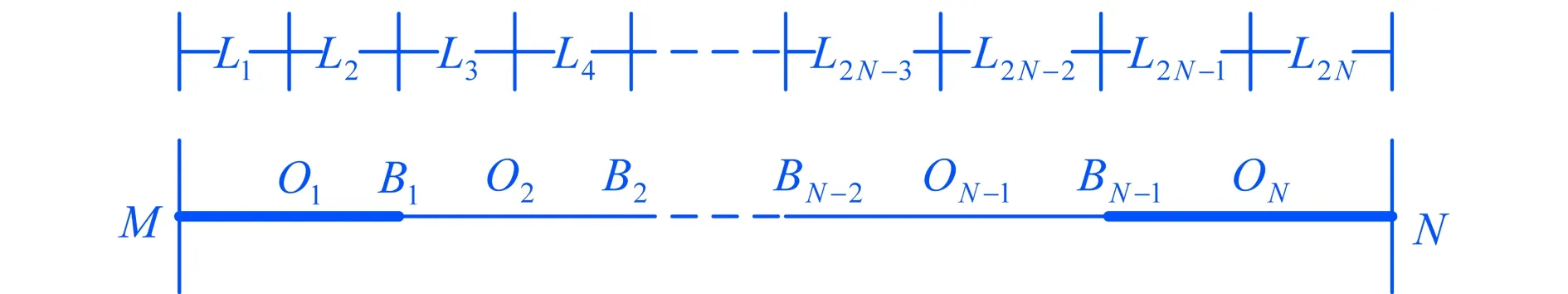
图4 含有2N段架空线与电缆的混合线路

2.2 主干线路故障区段定位

配电网典型架空线-电缆交替混合线路，M、N点装有行波测量装置.当n=1时，设每段线路的中间节点为O1、O2、O3…ON-1、ON；每段线路的末端节点(架空线与电缆连接点)为B1、B2、B3…BN-2、BN-1；将这段混合线路分为2N个区段，当节点O1、B1、O2、…ON-1B2、BN-1、ON分别发生故障时，记录初始行波到达M端与N端的时间并作差，其中架空线的行波传递速度为V1、电缆的行波传递速度为V2.

当线路末端节点发生故障时，故障行波初始波头到达线路两端时间差可表示为

(4)

当线路中间节点发生故障时，故障行波初始波头到达线路两端时间差可表示为

(5)

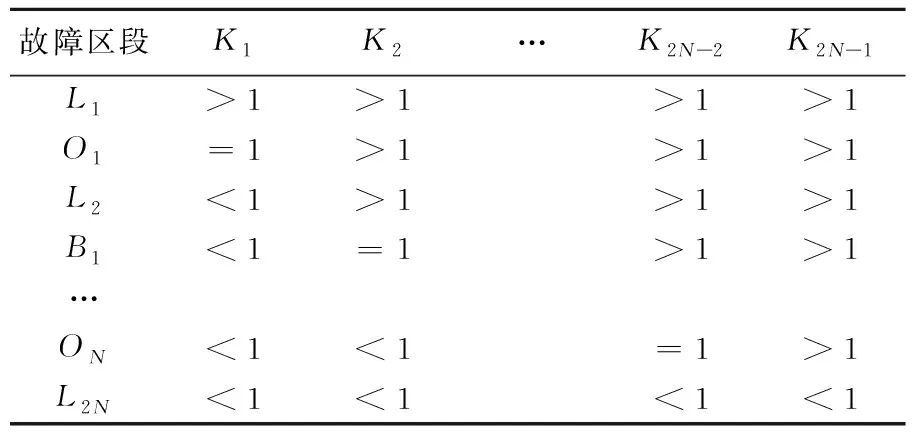
表1 不同故障区段内各节点理论与实际时间差比值

ΔTi为线路MN各节点故障前理论时间差，由线路长度和对应的速度求取，这样就构成了信息基准量矩阵.

设Ki=ΔTi/ΔT(i=1，2，…，2N-1)，故障区段不同时，由故障前理论时间差与故障初始波头时间差的比值可确定故障区段.

由表1可以得出结论：

如果Ki(i=1，2，3，…，2N-1)都>1，则故障发生在L1区段；

如果Ki(i=1，2，3，…，2N-1)都<1，则故障发生在L2N区段；

如果Ki(i=1，2，3，…，2N-1)等于1，当i为奇数时，故障发生在线路中间节点Oj处(j=(i+1)/2)；当i为偶数时，故障发生在线路末端节点Bj处(j=i/2)；

如果Ki<1，Ki+1>1，故障发生在Li+1区段内.

2.3 分支线路故障区段定位

若混合输电线路带有T接分支，1/2n区段法依旧可以判断故障区段.当n=1时，混合输电线路带有多条分支的情况，如图5所示.图5中，C11—CN-1N-1为分支线路中架空线路区段与电缆区段连接点；D11—DNN-1等为架空线路区段或电缆线路区段中点；P1—PN为各分支线路末端测量点.ΔT为故障前两节点若发生故障的理论时间差，Δt为故障后测量端接收到两节点行波波头对应的真实时间差.

图5 含T接多分支网络区段节点划分原理示意图

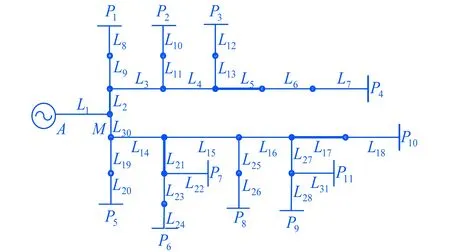
图6 10 kV配电网线路模型

计算原理同公式(4)、公式(5)，可推得：

当ΔtMN=ΔTMN，ΔtNPi=ΔTNPi，ΔtPiM=ΔTPiM时，故障发生于T型线路连接点Bi处.

当ΔtMN<ΔTMN，ΔtNPi=ΔTNPi，ΔtPiM>ΔTPiM时，故障发生于主干线路Bi-1Bi区段上.

若ΔtMN=ΔTOiMN时，故障发生于Bi-1Bi中点Oi处；若小于故障发生于Bi-1Oi区段；若大于则故障发生于OiBi区段.

当ΔtMN>ΔTMN，ΔtNPi<ΔTNPi，ΔtPiM=ΔTPiM时，故障发生于主干线路BiBi+1区段上.

若ΔtNPi=ΔTOi+1NPi时，故障发生于BiBi+1中点Oi+1处；若小于则故障发生于Oi+1Bi+1区段；若大于则故障发生于BiOi+1区段.

3 仿真分析

采用PSCAD/EMTDC搭建10 kV配电网混合线路仿真模型，如图6所示.L1为变电站至配电网接线，长度为15 km；L5、L17、L21为电缆线路，长度为3 km；其余线路为架空线，长度5 km.变电站Α处与各线路末端配有行波同步测量装置，采样频率10 MHz.由线路分布参数可知架空线路的行波波速为295 km/ms，电缆线路的行波波速为195 km/ms.

表2 线路参数

采用1/2n区段法，取n=3，每条线路分为8个区段，区段节点为O0-O8，如L1O2-O3表示为线路L1的3.75 km至5.625 km区段内.

设线路L15的2 km处发生单相接地故障，任选两测量端对数据进行分析，限于篇幅，表中仅含部分数据.

表3 故障线路定位

(续)表3

根据仿真结果，可以看出当测量端按一定规律排列的情况下，连续测距结果对应的支路不相同或无测距结果，则对应的最短传输路径不包含故障支路；若可由两测量端初始行波到达时差得到定位结果，且多个数据显示对应的最短传输路径包含同一支路时，则该支路为故障支路.定位故障支路后，对线路区段进行合理划分，真实测量的初始行波波头时差会落在某两个节点故障理论时差区间内，进一步缩小故障搜索范围，若真实波头时差靠近理论时差区间边界，则考虑搜索相邻线路.

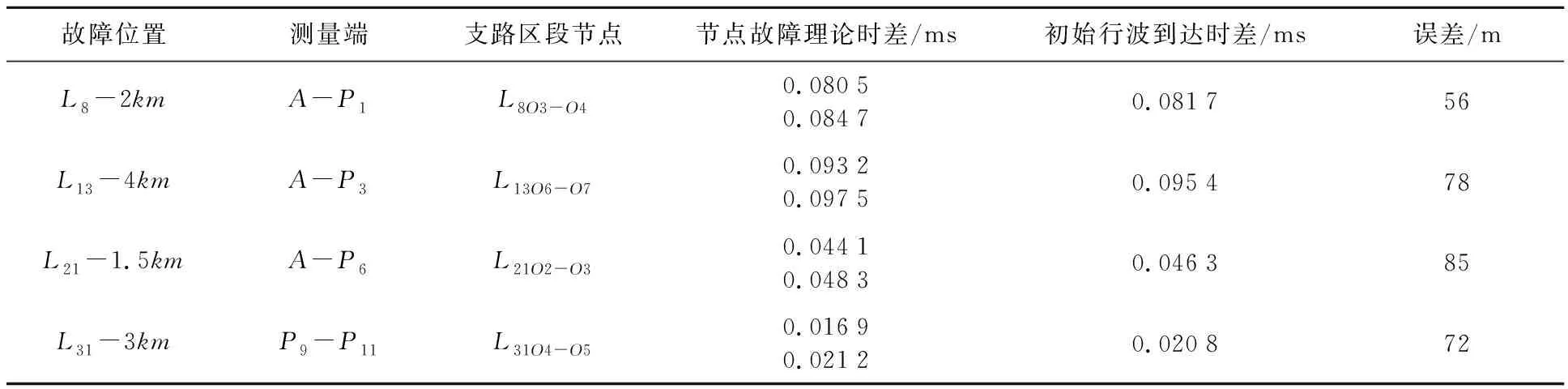
表4 不同故障位置定位结果

4 结 论

本文分析了行波测距在配电网应用时可能出现的问题，在此基础上提出了一种区段划分方法，有效缩短了故障查找范围，并配合传统行波法进一步定位故障点，原理简单，提高了线路检修效率，仿真结果验证了方法的有效性；

本文提出的测距方法需要每条分支末端装有同步测量装置，这样加大了成本，但是随着对布点优化的研究及相关技术的发展，可以降低成本过高的问题；当测量结果落在理论区段边界时，可能出现故障支路误判，可以通过降低误差解决这一问题.