面向智能用电的家庭微网能量优化研究

黄亚峰，何 威，刘思驿

(东北电力大学电气工程学院，吉林 吉林 132012)

随着分布式光伏发电设备的普及程度越来越高，家庭用电设备朝着智能化方向发展，住宅领域的用能结构正在发生重大改变.普通用户不再仅仅充当消费者的角色，而是向着具有一定调节能力的家庭微网方向转变.如何充分利用分布式能源优化用能结构，节省用电成本，成为当下研究的热点[1-4].

目前，国内外学者关于家庭微网的用能结构优化问题已有大量的研究和成果.文献[5]以家庭最大盈利为目标，建立基于光伏出力预测的家庭能量协调调度模型，但是该文献设置用能场景单一，无法充分说明分布式光伏和储能系统对用能结构带来的影响.文献[6]利用线性加权法将多目标问题转化为单目标来求解，但在加权系数的选取时有较强的主观性.文献[7]未加入分布式能源，仅对温控负荷及电动汽车进行建模，无法保证模型可以推广到包含分布式光伏以及储能系统的用能环境.

基于上述分析，本文从用户角度出发，建立了整合可再生能源发电以及储能系统的能量管理优化模型，将光伏和储能整合到住宅领域.通过对储能系统和用电设备进行能量管理以实现用电成本最小化的优化目标.以此模型为基础，在3种不同用能场景下从能量消耗、用电成本和峰均比等方面对模型进行了评估，验证了模型的正确性和有效性.

1 数学模型

在本节中，给出了光伏系统、储能系统的数学模型和约束条件以及峰均比的概念.在此基础上，提出了优化问题.

1.1 分布式光伏系统数学模型

光伏发电机组输出的有功功率取决于光伏电站处的太阳辐射强度和环境温度，计算公式为[5]

(1)

公式中：PPV为光伏系统输出功率；PSTC为标准条件下光伏系统输出的最大功率；IM为入射到光伏系统的辐照度；ISTC为标准测试条件下的辐照度(ISTC=1 kW/m2)；k为功率温度系数，取自光伏模块数据表；TSTC为参考温度(TSTC=25 ℃)；TM为光伏组件温度，可近似表示为

(2)

公式中：Tamb为环境温度；εPV为光伏组件相关的比例常数.

1.2 储能系统数学模型

小容量储能系统(Energy Storage System，ESS)用于存储光伏发电系统产生的部分电能，主要是为了更有效地利用光伏能源.ESS的荷电状态(State Of Charge，SOC)是优化家庭微网运行的关键变量，需要实时监控.SOC随ESS充电和放电过程的变化为

(3)

(4)

公式中：SOC(t)和SOC(t-1)分别为对应时刻ESS荷电状态；PESS(t)为储能系统输出功率(当ESS充电时，PESS(t)>0；当ESS放电时，PESS(t)<0)；∂为ESS自身放电率；ηc和ηd分别为ESS充电和放电效率；EESS(t)为储能系统容量.

在能量管理系统经济运行过程中，ESS单元频繁的充放电行为会对其使用寿命和性能造成一定的损耗，本文用运行维护成本(CESS，om)来表征这些损耗.

CESS，om=|PESS(t)|·KESS，om，

(5)

公式中：KESS，om为ESS单元的运行成本系数，

为了延长ESS使用寿命，避免过度充放电，ESS中储存的电量和充放电功率不应超过制造商规定的限度.

SOCmin≤SOC≤SOCmax，

(6)

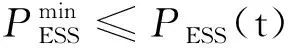
(7)

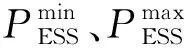
1.2 峰均比

峰均比(Peak to Average Ratio，PAR)是某个时间段内最大总负载与总负载平均值的比值.PAR可反映消费者的能源消费行为和家庭微网的运行情况，提高PAR会危害微网内部稳定，增加用电成本.相反降低PAR会提高用电的稳定性和可靠性，降低用户用电成本.PAR可表示为

(8)

(9)

公式中：Lpeak和Lavg分别为一个优化周期T内最大总负荷和平均负荷；Etotal(t)为用电设备在t时刻的总能耗.

(10)

2 面向智能用电的家庭微网能量优化研究

本文提出的优化模型在满足设备运行约束条件下，考虑可再生能源发电和储能系统，通过对用电设备启停时段进行最优调度，使用电成本最小化.优化模型的一般形式为

minf

s.t.用电设备i的操作约束，∀i∈A，

其中，f代表家庭微网总用电成本，可用公式(11)表示；A为优化调度的用电设备的集合.由于优化调度主要通过调整用电设备的开启时段来节约用电成本，本文仅考虑可转移负荷的优化情况，不可转移负荷不在本文研究范围.

(11)

公式中：λ(t)为t时刻电价信息；Si(t)为t时刻对应设备开启状态；Si(t)=0表示处于待机状态，Si(t)=1表示设备处于开启状态.上式第一项表示负荷消耗的总功率，第二项表示光伏和储能系统总功率.同时，优化过程还需满足以下约束为

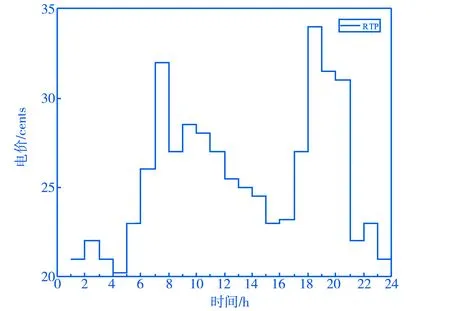
图1 实时电价

PARopm≤PARunopm，

(12)

fopm≤funopm，

(13)

(14)

在电力市场中，有多种不同的电价模式用来确定一天的电能价格，如实时电价(RTP)、分时电价(TOU)和尖峰电价(CPP)等.由于在电网运行过程中，RTP比其他价格信号表现得更加灵活，更有利于针对性的在非高峰时段安排能源消耗来降低用电成本.本文采用PJM公司提供的实时电价信息来指导用电行为，实时电价信息，如图1所示.

3 基于二进制粒子群算法的模型求解方法

传统的优化方法不能处理大量的用电设备，并且在收敛上面临很多困难.而且，传统算法大多不具有全局视角，往往收敛于局部最优解.本文采用二进制粒子群算法(BPSO)实现用电设备的优化调度问题.

粒子群算法(PSO)是一种在搜索空间内寻找最优解的自然优化算法.PSO算法本质上存在于连续域中，其在离散域的变体是BPSO.BPSO算法主要取决于四个因素：初始位置、初始速度、粒子自身的最佳位置和全局的最佳位置.在该算法中，种群被随机初始化并分散在搜索空间中.粒子的初始位置和速度分别用xi=x1+x2+…+xI和Vi=V1+V2+…+VI表示.利用公式(15)更新每次迭代的粒子速度.

(15)

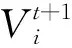
(16)

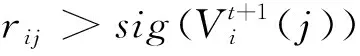
在每次迭代中，粒子记录它们相对于相邻粒子的位置，找到的局部最佳位置表示为Xlbest=Xlbest1+Xlbest2+…+XlbestN，然后将局部最优值相互比较，以找到全局最优位置.如果满足目标函数，则粒子中的g粒子称为全局最优位置，全局最优位置表示为Xgbest=Xgbest1+Xgbest2+…+XgbestN.使用全局最优值而不是局部最优值的主要原因是它更快地收敛到最优解.全局最优值是一个二进制编码字符串，表示设备的最佳开/关状态.

4 算例分析

4.1 算例描述

为了验证所提出的模型性能，考虑了一个拥有主要家用用电设备以及光伏发电系统和储能系统的用电场景.设备额定功率和使用情况，如表1所示.优化区间为24小时，时间间隔ΔT=1 h.假定外部电网电源全天可用，以满足用户用电需求.为提高分布式能源的利用率，减少对外部电网的冲击，ESS在白天只从PV系统充电，完成充电后，在一个电价较高的时段放电供家庭微网使用.储能系统运行参数，如表2 所示.采用的BPSO优化参数，如表3所示.

表1 用电设备基本参数

表2 储能系统运行参数

表3 BPSO优化参数

为了更加全面分析模型性能，设置三种不同用能场景：

(1)case1：无PV和ESS参与且未进行用电优化；

(2)case2：有PV和ESS参与但未进行用电优化；

(3)case3：有PV和ESS参与并且经过用电优化.

4.2 结果分析

用电设备各时段能耗情况，如图2所示.可以看出，在第一种场景下，用电高峰时段主要集中在0时～2时以及21时～22时，高峰负荷分别为5.68 kW和4.65 kW.在第二种场景下，将PV和ESS集中到能源模型中，在7时～18时间段，系统可从PV系统获得可再生能源，一部分用于储能系统充电，另一部分供用电设备使用.可以发现，在9时左右用电高峰时段，由于ESS放电的影响.负荷减少74.37%.从场景3经过优化后的负荷分布可以看出，峰值负荷出现的时段明显少于未经优化的场景，负荷有明显的的转移现象，在18时～20时电价较低时段，场景3的负荷较其他两种场景增加37.92%和32.76%.

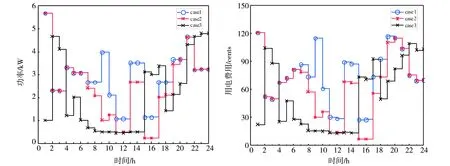
图2 能量消耗 图3 用电费用

三种场景用电费用，如图3所示.可以看出，场景2由于加入光伏和储能系统，用电费用显著降低，其中，在时段9由于光伏系统是可用的，用电费用减少73.68%.与场景1相比，场景2总用电费用减少56.67%.场景3经优化用电处理后，由于在电价高峰时段负荷转移的影响，此时段用电费用明显低于场景1、场景2，总用电费用相较于场景2降低了19.61%.

表4 不同用能场景下的PAR

三种场景的PAR，如表4所示.由表4可知，场景2加入可再生能源和储能系统后，PAR降低了11.42%，与未经优化的场景相比，经优化后场景3的PAR降低了8.46%，主要是因为优化后大部分高峰期负载被转移到非高峰时段，这不仅降低了用电成本，而且还提高了系统的稳定性和可靠性.

5 结 论

针对典型家庭用电设备用能优化问题，本文提出了一种将光伏系统和储能系统融合到住宅领域的家庭能量管理优化方案.研究的主要目标是用电成本最小化，同时尽可能减小用电设备能耗的峰均比.结果表明，融合可再生能源以及储能系统的优化方案能够更可靠、高效的降低用电成本以及峰均比，这也有助于提高电力系统稳定性，保证电网稳定可靠运行.