对数自回归条件久期模型的统计推断

韩 玉，田宝成，王书鹏

(东北电力大学理学院，吉林 吉林 132012)

针对时间间隔不规则的金融高频或超高频数据，1998年，Engle和Russell[1]首先提出了一种刻画交易过程的久期模型，自回归条件久期(ACD)模型.根据模型假定的不同，ACD模型可分为指数ACD(EACD)模型、威布尔ACD(WACD)模型、伽马ACD(GACD)模型等.2013年，Xu[2]提出了对数正态ACD(LNACD)模型.实验表明，LNACD模型在刻画金融高频数据上更优于EACD和WACD模型.2016年，Zheng[3]等利用渐进ACD(FACD)模型对香港交易所和伦敦交易所的板块交易久期进行分析，并证明了其有效性.逐渐地，模型在形式上也有了创新，一些非线性久期模型陆续被提出，典型的有对数自回归条件久期(Log-ACD)模型[4]，Box-Cox ACD模型[5]，阈值ACD(TACD)模型[6]等.文献[7]已推导出Log-ACD模型的一些渐进性质，本文便是基于Log-ACD模型进行进一步研究.

最小二乘法是一种常用的估计方法，通过最小化误差平方和得到参数估计量.Zhao[8]等基于最小二乘估计给出了Log-ACD模型的渐进性质.1988年，Owen[9]提出了一种非参数统计推断方法，经验似然方法.运用该方法可以构建经验似然比检验统计量，进而给出估计参数的置信区间.此方法一经提出，便被学者广泛关注和研究，Ling[10]应用经验似然于广义自回归条件异方差(GARCH)模型，Qin[11]等推断出了经验似然估计量的渐进性质.

1 模型介绍

本文基于对数自回归条件久期(Log-ACD)(1，1)模型进行研究，模型形式为

xt=eψtεt，ψt=ω+αlnxt-1+βψt-1，

(1)

公式中：xt为金融久期，满足xt≥0；ψt为久期xt以x1，…，xt-1为条件的期望.

记θ=(ω，α，β)T∈Θ，Θ为模型(1)的参数族.对于任意θ=(ω，α，β)T∈Θ，假设

(C2)Elnεt=0，E(lnεt)2<.

2 主要结论

假设θ0∈Θ是模型(1)的真参数，x1，x2，…，xn表示一组时间久期，令

lt(θ)=(lnxt-ψt(θ))2，

(2)

(3)

(4)

(5)

构建对数经验似然函数

(6)

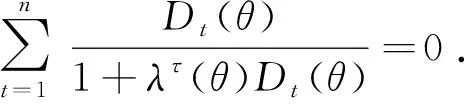
我们提出原假设H0：θ=θ0，为了检验此假设，构造经验似然比统计量

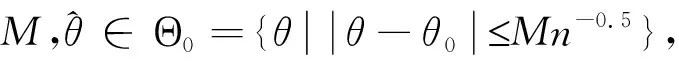
公式中：

定理2若假设条件及定理1成立，则在备择假设条件下，当n→时，有

引理1若假设条件成立，则有

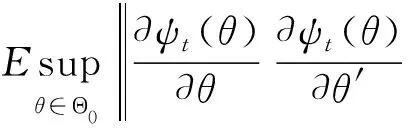
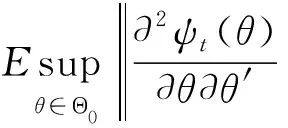
引理2若假设条件成立，则有

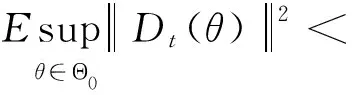
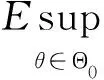
引理3若假设条件成立，在邻域Θ0={θ||θ-θ0|≤Mn-0.5}内，当n→时，有

公式中：

3 数值模拟

此节针对Log-ACD(1，1)模型

进行数值模拟，公式中：ω=0.7，α=0.2，β=0.3.

3.1 Bootstrap抽样

在总体样本信息未知时，通常是从总体样本中摘取一部分样本进行参数估计，这样可能并未完全利用样本中的信息.Bootstrap重抽样，是指从总体样本中有放回地多次抽取，从而得到的新样本的方法.该方法可能会多次提取某一个样本，如此便能充分地利用样本信息，进而进行后续研究.Bootstrap抽样利用了样本的剩余价值，是能够利用小样本估计总体的非参数方法.

下面根据不同模型假定、样本容量n及重复抽样次数m，在置信水平为0.05的情况下，分别计算常规抽样和Bootstrap重抽样方法构建经验似然比检验统计量的覆盖率，结果如表1和表2所示.

表1 模型假定为μ=0，σ2=1的对数正态分布时经验似然与Bootstrap抽样的覆盖率

表2 模型假定为参数为1的指数分布时经验似然与Bootstrap抽样的覆盖率

表1和表2显示，当模型假定为对数正态分布和指数分布时，随着样本量的增加，经验似然比检验统计量的覆盖率愈加贴近置信水平.因此，Bootstrap方法并不适用于经验似然，经验似然方法效果更佳.

3.2 经验似然比统计量

此节针对模型假定为μ=0，σ2=1的对数正态分布，重复试验500次和1000次，在置信水平为0.05的情况下，分别计算最小二乘估计的渐进正态性得到的卡方分布检验统计量和经验似然比检验统计量的覆盖率，结果如表3所示.

表3 各统计量的覆盖率

根据表3的结果可知，当模型的误差项服从对数正态分布时，经验似然估计较最小二乘估计更贴近于置信水平，且更加稳定.因此，对于Log-ACD模型的参数估计研究，经验似然方法更优于最小二乘法.

4 附 录

证明引理1：

首先

根据式(1)，可得

(7)

根据式(7)，可得

(8)

当n→时，

再由Cauchy不等式，

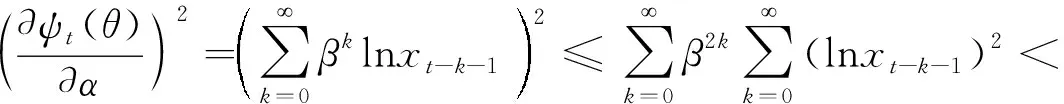
因此，结论(1)成立.

由(8)可得

证明引理2：

首先

根据假设条件(C2)和引理1，可知结论(1)成立.

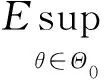
根据引理1和假设条件(C2)，有

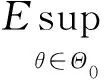
证明引理3：

根据引理2的结论(2)，有

由假设条件C2和引理1(2)可得

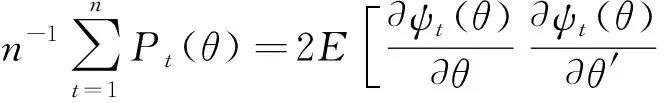
则结论(1)成立.类似地，可知结论(2)成立.

证明定理1：

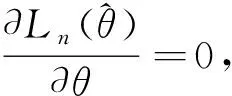
根据引理3的结论(2)可知，当n→时，

对于序列{Dt(θ0)}，有

E[Dt(θ0)|Ft-1]=0 ，

公式中：Ft-1表示序列中包含D1(θ0)，…，Dt-1(θ0)的历史信息，因此序列{Dt(θ0)}为鞅差序列.根据鞅差中心极限定理可知，当n→时，

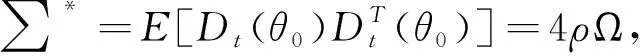
证明定理2：

根据文献[6]可得