源于教材 高于教材
——对两道高考题的探“源”觅“流”
◇ 谢迁尔
苏联数学教育家奥加涅相说过:“必须重视,许多习题潜藏着进一步扩展其教学功能、发展功能和教育功能的可行性.”研究近十年的高考真题,就会发现很多题目“似曾相识”,总能在高考真题中找到课本习题、例题的影子.高考试题“源于课本”,这是由高考的性质决定的.高考的命题都应遵循“立足基础,考查能力”这一重要原则.自然寻找高考数学试题的课本生长点、命题背景,探究题源,挖掘命题的“题根”,可以达到由例及类、触类旁通的目的.下面就以两个高考题进行探“源”觅“流”.
1 真题再现
例1(2014年新课标卷Ⅱ)设向量a,b满足则a·b=( ).

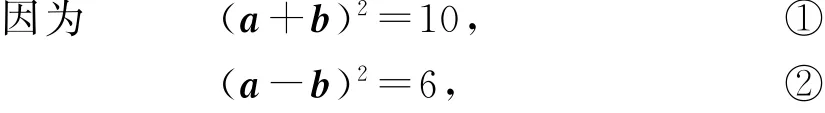
由①-②,得a·b=1.
例2(2017年新课标卷Ⅱ)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则PA→·的最小值是( ).
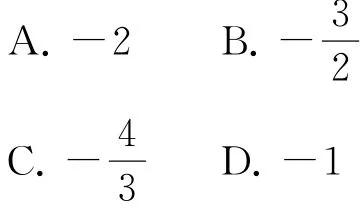
如图1所示,取BC的中点D,取AD的中点E.
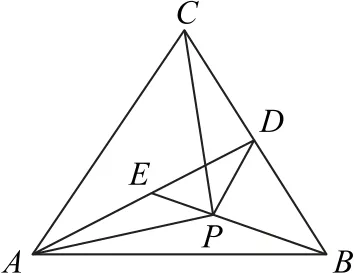
图1
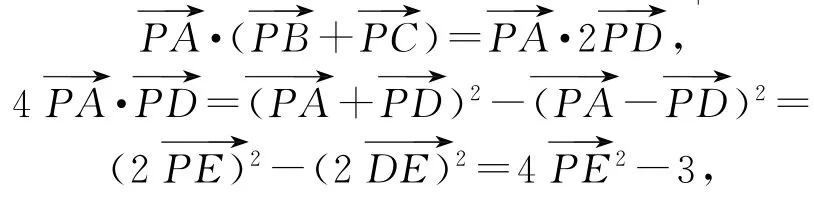
本题解法中,同样也是利用到例1提及的公式.
2 寻根溯源
上述两个问题的背景是普通高中课程标准实验教科书《数学必修4》A版第108页习题24中的A组第3题.
题目已知|a|=2,|b|=5,a·b=-3,求|a+b|,|a-b|.
通过这个题目的分析及课本例题2中证明:
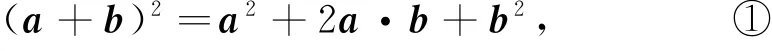
再将(a+b)2=a2+2a·b+b2中的向量b换成向量-b,又有
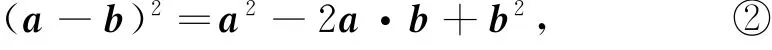
式①-②,可得
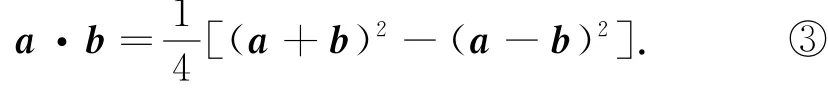
3 把握根本
式③就是著名的“极化恒等式”.
1)平行四边形模式:
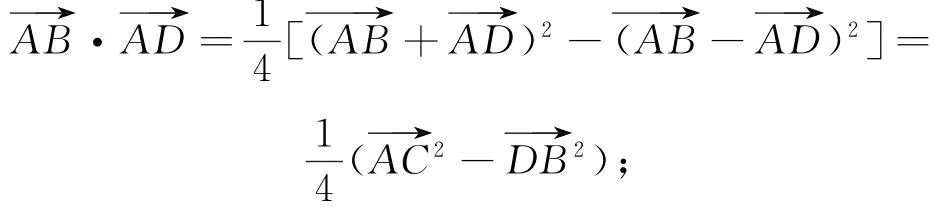
2)三角形模式:在△ABD中,AM是BD边上的中 线
极化恒等式的作用在于把数量积转化为“和向量”与“差向量”,因此当两个向量的“和向量”或“差向量”为定向量时可以应用极化恒等式进行转化.此恒等式的精妙之处在于建立向量与几何长度(数量)之间的桥梁,实现向量与几何、代数的巧妙结合.
4 舒展枝叶
从上面的分析,我们可以看到极化恒等式作为代数和几何的桥梁,具有化动(动点)为定(定点)、化动(动态)为静(静态)、化曲(曲线)为直(直线)、化普通为特殊的能力,所以在各地历届的高考题和模拟试题中得到广泛应用.
4.1 处理长度的问题
例3已知圆O:x2+y2=4,直线l与圆O交于P,Q两点,A(2,2),若AP2+AQ2=40,则弦PD的长度的最大值为取PQ的中点M,则化简得.要使得最大,当且仅当最小,即时,即时成立.即P(-2,0),Q(0,-2)时成立,所以
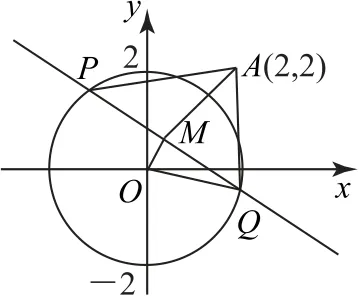
图3
4.2 求数量积的最值
例4已知等边△ABC内接于圆O:x2+y2=1,且P是圆O上一点,则的最大值是( ).

设D为BC的中点,M为AD的中点,则
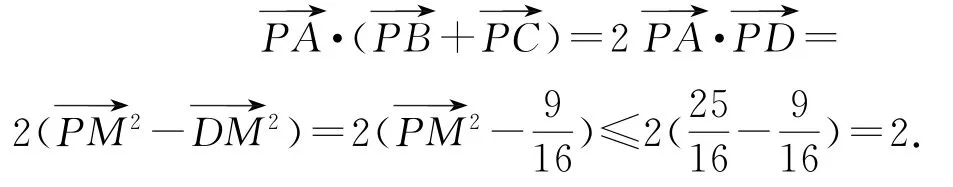
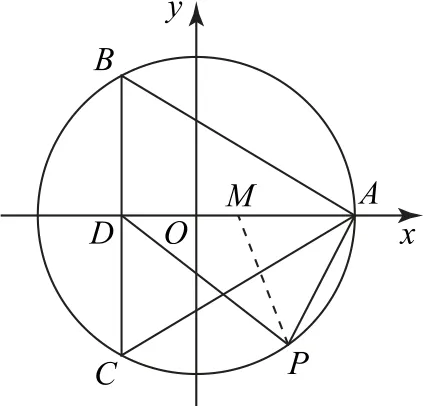
图4
4.3 结合圆锥曲线,迁移应用
例5已知AB为椭圆的一条动弦,且经过原点,M为直线3x-4y-15=0上的一个动点,则的最小值为( ).
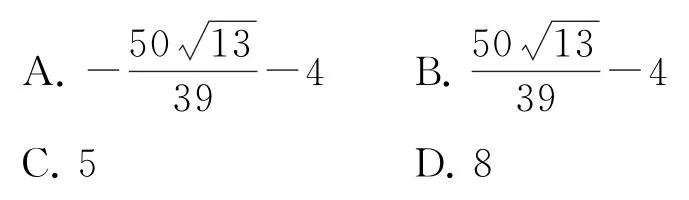
这个问题的破解难点就是A,B为椭圆y2=1曲线上的动点,连接MO,根据极化恒等式可得,这样考虑到取最小值且取最大值时,曲线动点问题便得以化解.
如图5所示,设d为点O到直线3x-4y-15=0的距离,则等于椭圆的长半轴长2.因此,
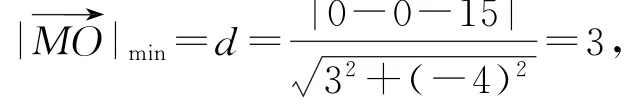
综上所述,选C.
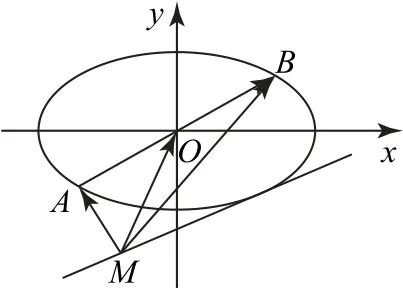
图5
通过两道高考真题的研究,寻根溯源,发现所有的高考题都会遵循一个重要规律:教材是高考题的发源地.一个不变原则就是“取材于课本,但又不拘泥于课本”.课本中每一个例题、习题的设置都有其目的和作用,许多高考题都能在课本上找到“根源”.不少高考题就是课本原题的变形、改造和整理.因此,平时的复习中,应充分发挥课本上典型例题和习题的作用,提高学习效率,达到事半功倍的学习效果,切实减轻学生过重的学习负担.

