数学方法在有机化学中的应用

◇ 罗维凤

数学作为基础学科在其他学科中的应用很广泛，为了使学生能够更好地理解有机化学知识，教师要善于利用数学方法来指导学生，使学生能够掌握解题策略和解题方法，灵活地解决问题．

1 平均值法，简化计算

化学中的计算是非常烦琐而且复杂的，稍有计算错误就会影响整道题的解答．教师可引导学生采用平均值法简化计算，达到快速而准确答题的目的．

例1燃烧0．1mol两种气态烃的混合物，生成3．584LCO2(标准状况)和3．60g水，则混合气体中( )．

A．一定有甲烷 B．一定有乙烷

C．一定无甲烷 D．一定有丙烷

分析通过思考，学生会想到设两种气态烃的平均分子式为CxHy，根据烃燃烧的通式算得x＝1．6，y＝4，即平均碳原子数为1．6，而碳原子数小于1．6的烃只有甲烷，所以一定有甲烷．

解题过程中利用了平均值的方式来计算，把化学问题转化为数学问题，使学生可以由此及彼，方便了答题．

2 十字交叉法，巧用关系

在计算二组分混合物平均量与组分量的问题时，若满足M1·n1＋M2·n2＝M·n，均可按十字交叉法计算．M表示平均相对分子质量，M1、M2表示两组分各自的相对分子质量，n1、n2表示两组分在混合物中所占的物质的量分数，则n1∶n2等于两组分的物质的量之比，有时也可以是两组分的质量之比．

例2在常温下，将1体积乙烯和一定量的某气态未知烃混合，测得混合气体对H2的相对密度为12，求这种烃所占的体积．

分析根据题意得，混合物的平均相对分子质量为24，相对分子质量小于24的烃只有甲烷，所以一定有甲烷．

根据十字交叉法有:

故该烃为甲烷，体积为乙烯的一半．

通过十字交叉的方式，巧用关系会促进学生理解化学中各物质的量，从而完成计算，快速解题．

3 差量法，把握差值

在一些根据化学方程式的计算中，给出的条件是反应前后的差值，这类问题用差量法解决十分简便．解题过程中，学生首先分析形成差量的原因；然后找出差量与已知量、未知量间的关系；最后列比例式求解．

例3amL三种气态烃的混合物与足量氧气混合点燃爆炸后，恢复到原来的状态(常温、常压)，体积共缩小2amL，则三种烃可能是( )．

分析可以设两种气态烃的平均分子式为CxHy，根据烃燃烧的通式可以写出如下关系式:

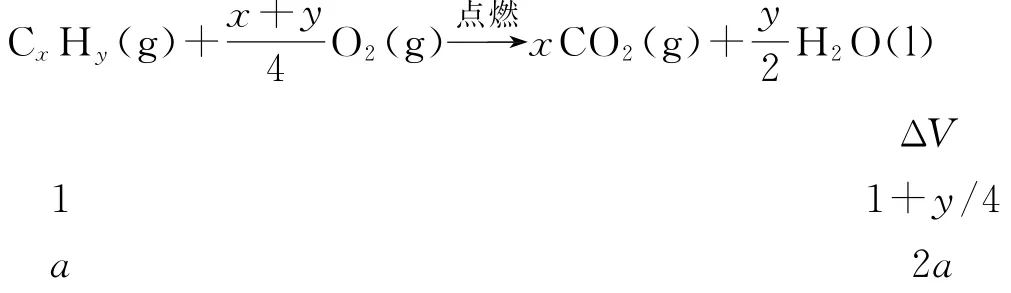
计算得y＝4，平均氢原子数为4，所以选A．

4 数列法，探究规律

化学变化如果是有规律的，教师则可以引导学生采用数列法，通过探究其中的变化规律来分析解题思路和解题方法，实现对问题的快速解答．

例4下列稠环芳烃，它们虽然不是同系物，但其组成和结构都是有规律变化的:

分析通过看图学生会发现(Ⅰ)、(Ⅱ)、(Ⅲ)的分子式分别为C10H8、C16H10、C22H12．分析发现前后两项碳原子数、氢原子数成等差数列，设通式为CaHb，利用数列法进行求值:a1＝10，a2＝16，a3＝22，an＝10＋(n－1)×6＝4＋6n．通过计算会算出b1＝8，b2＝10，b3＝12，bn＝8＋(n－1)×2＝6＋2n，所以通式为C4＋6nH6＋2n，则第25个物质分子式为C154H56．

解题过程中，学生用到的就是数学中的数列知识，根据已知化合物的分子式来设“通项公式”，利用数学通项公式的求解方法就可以顺利答题．

5 几何思想，直观形象

数学中的几何思想具有直观形象的特点，能使学生一目了然地看到各种数量关系，明确知识间的联系，看到知识的来龙去脉．教师要善于引导学生把抽象的化学知识和化学变化变成形象具体的几何图形，借助直观的图象来分析和探究化学知识．在教学过程中，教师要向学生渗透几何思想，引导学生把抽象的知识转化为形象的图形，通过直观观察的方式来学习．在判断原子共面问题时，学生需要注意以某一基团为基准向外延伸，如苯环、碳碳双键、碳碳三键，通过几何绘图，学生会构建出直观的形象，在绘图中理解规律，形成客观的认识．

例5如图1所示，在同一平面上碳原子最多有几个?

分析可以以苯环为基准向外延伸，苯环上的6个碳原子以及第2、5号碳原子在同一平面Ⅰ内；以碳碳三键为基准，第1、2、3号碳原子在同一直线上，即第2、3号碳原子所在直线属于Ⅰ，所以1号碳原子也在Ⅰ内；以碳碳双键为基准，4、5、6、7号碳原子在同一平面Ⅱ内，4、5号碳原子既在平面Ⅰ内又在平面Ⅱ内，两点决定一条直线，4、5号碳原子所在直线既在平面Ⅰ内又在平面Ⅱ内，两面共线可能相交也可能重叠，所以所有的碳原子可能共面．

通过直观观察，学生会清楚地看到各种化学关系，有利于学生借助几何图形的帮助在形象的图片中看到化学知识，提高理解能力，强化认识．

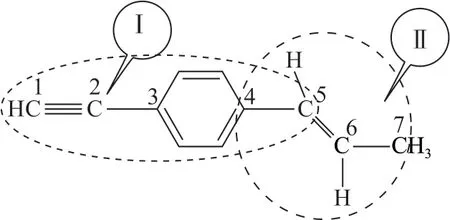
图1

总之，在化学计算中，若能够巧妙灵活地应用这些数学方法，可以化难为易、化繁为简．教师要多从解题方法上引导学生，对学生进行“授之以渔”的教育，让学生能够掌握技巧，灵活地应用数学方法解决化学问题，促进学生解题能力的提高和高效课堂的实现．