“作、识、用”三管齐下函数图像巧掌握

◇ 许 陈

函数图象是函数的一种表达形式，它形象地显示了相应函数的本质属性，在实质上与函数解析式是相同的．函数可以把图象精确化、细微化，反之图象能使函数直观化、形象化．高中对函数图象的要求有三个方面:作图、识图、用图．作图是基本能力，识图是综合素质，用图是最终目标．

1 作图

高中阶段主要利用描点法作图．函数的图象通常是一些连续的曲线或直线，但有时它也可能是几段光滑曲线，也可能由一些孤立点或几段线段组成，还可能由折线或射线来构成．

例1函数f(x)＝x2＋1，试作出对应的图象，并比较f(－2)，f(1)，f(3)的大小．

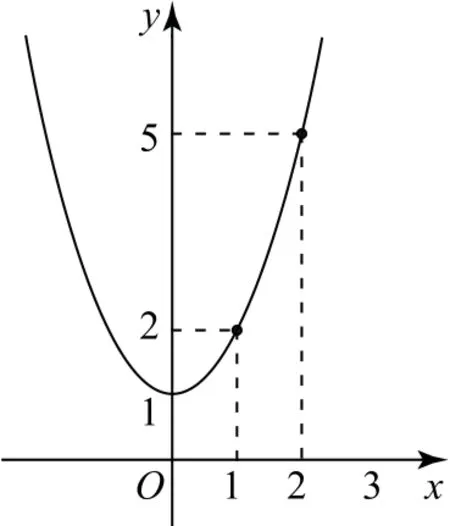
图1

通过描点法作出函数f(x)＝x2＋1的图象，如图1．其步骤是列表、描点、连线．注意其中的特殊点(0，1)，这时函数取最小值．

结合图象的特征，在第一象限内，y随着x的增大而增大，则有f(1)＜f(2)＜f(3)，容易发现f(－2)＝f(2)，即f(1)＜f(－2)＜f(3)．

掌握函数图象描点法的三步骤，结合函数图象中特殊点的大小关系或图象本身的特点，从“数”与“形”两个角度出发，判断不同自变量所对应的函数值的大小关系．画函数图象要先求定义域，然后在定义域内找特殊点，比如，端点、断点和极值点，并注意函数的图象变化趋势．

2 识图

对于给定的函数图象，要能从函数图象的分布范围、变化趋势、对称性等方面研究函数的定义域、值域、最大值、最小值等有关问题．

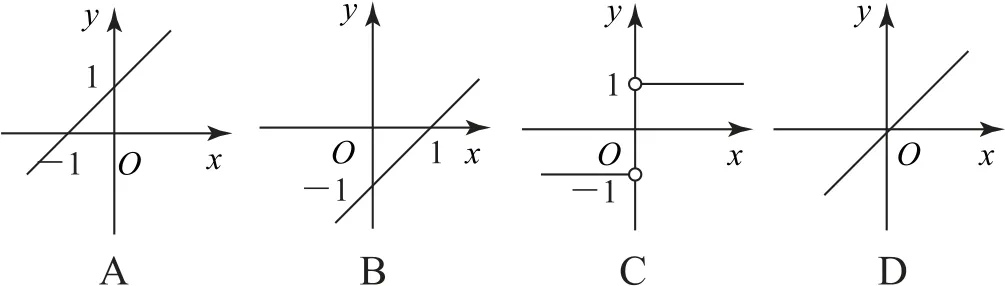
例2函数的图象是( )．

所给函数可化为

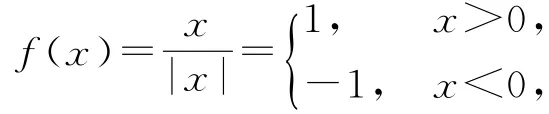
故对应的图象为C．

其实本题也可以直接根据函数的定义域{x|x≠0}，结合待选图象的特征，加以准确识图作出正确判断．在解答这类问题时，关键是抓住题目相应的量与量之间的对应关系和变化规律，结合初等函数的相应规律进行分析与判断．

3 用图

函数图象形象地显示了函数的相关性质，为研究数量关系提供了“形”的直观性，是探求解题途径、获得问题结果的重要工具．

例3设x∈R，求函数的最小值．

当0＜x＜1时，函数为反比例函数

图象的一段；当x≥1时，函数为直线y＝x图象的一段．从而可得到函数图象(如图2)，结合图象可知，函数的最小值为1．

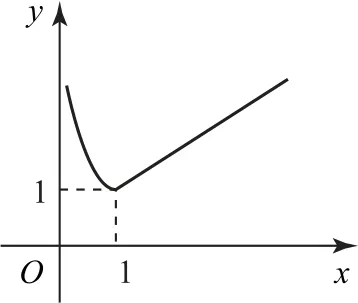
图2

此类问题通过数形结合可以非常直观明了地判断对应的最值问题．要注意作图的准确性，特别是端点和分段点的位置，只有保证作图的准确性，才能准确用图，为解题带来方便．

高中数学中，作图是函数的基本技能之一，通过作图为识图和用图提供直观依据，而识图又可以更精确、更有目的地用图．用好函数图象是最高目标，可以用来求解函数值、函数定义域、值域等相关问题，也可以用来处理一些与函数性质有关的其他问题．