数字化铸造砂型五轴联动成形控制技术研究
彭宝营,单忠德,刘 丰,侯明鹏,戴文强
(机械科学研究总院集团有限公司 先进成形技术与装备国家重点实验室,北京 100044)
0 引言
与传统铸造相比,数字化无模铸造精密成形技术利用加工砂型作为型腔或砂芯,无需木模、金属模具,具有污染少、周期短、成本低等优势[1-2],已成为快速绿色铸造领域的重要发展趋势。随着无模铸造技术的发展,越来越多复杂薄壁铸件如叶轮、异形舱体、复杂壳体等,采用砂型无模铸造,复杂砂型、砂芯需要五轴联动成形[3-4]。五轴联动加工是在X轴、Y轴、Z轴3个线性轴的基础上增加了2个旋转轴,用于刀具或工件的旋转。由于旋转运动的存在,为确保刀尖点始终位于编程轨迹上,控制系统需要实时调整旋转轴中心的位置,即具有旋转刀具中心(Rotation Tool Center Point, RTCP)控制功能[5-6],也称为“刀尖点编程”。作为高档五轴联动数控系统的核心功能,RTCP已成为众多企业的核心技术。目前,五轴联动控制技术的研究主要集中在金属切削领域,RTCP的研究以仿真为主[7-8]。开放式控制系统,如可编程多轴控制器(Programmable Multi Axes Controller, PMAC),建立在PC机平台上,可自定义编写正逆解和伺服算法程序,在五轴联动系统开发方面具有巨大的优势。
复杂薄壁构件铸造砂型常常需要几天才能加工完成,为缩短铸型生产周期,迫切需要提高成形效率。而砂型加工切削力较小,也使砂型高速成形成为可能。高速进给加工过程中,遇到超速或加工尖角情况时,前瞻控制通过对加工程序的超前处理,在精度允许的范围内预先调整加减速,使运动速度不高于极限值,一直保持在电机和装备的许可能力之内[9-11]。因此,前瞻技术已成为高速进给加工的关键技术之一[12-13]。在五轴联动高速加工前瞻控制方面,一些学者从速度、加速度、加加速度最大值约束的角度,研究了五轴加工轨迹前瞻插补算法[14-16];文献[17]分析了五轴加工过程中各轴速度、加速度之间的限制关系,提出了前瞻缓冲区处理办法;文献[18]研究了五轴联动非均匀有理B样条插补中的速度前瞻控制技术。为实现铸造砂型五轴联动快速成形制造,本文推导了B-C双摆头结构五轴联动RTCP运动学模型,分析了五轴联动加工过程速度波动机理,提出了砂型五轴联动高速成形单轴前瞻控制方法,并基于PMAC控制系统进行了实验验证。
1 砂型五轴联动成形RTCP运动学模型
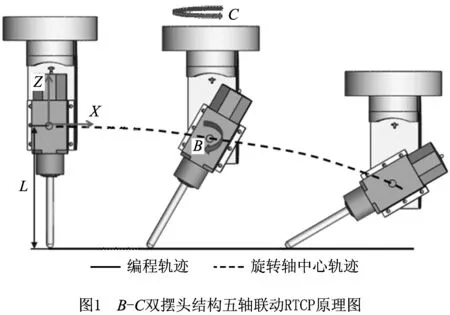
双转台结构五轴机床加工零件尺寸较小,而砂型以型腔为主,尺寸较大,适合采用双摆头结构。双摆头五轴装备主要有A-C、B-C两种组合结构[19],本文选取B-C双摆头结构,进行砂型五轴成形控制技术研究。B-C双摆头结构五轴联动RTCP原理图如图1所示,当编程轨迹为一条直线时,B轴或C轴转动时,为维持刀尖点沿直线轨迹运动,需要实时调整X轴、Y轴、Z轴位置,对刀尖点的位置偏移进行补偿。
建立B-C双摆头结构砂型五轴联动成形坐标系示意图,如图2所示。其中,OMXMYMZM是砂型工件坐标系,原点OM为工件轮廓的特征点,通常与CAM软件设置的原点保持一致;OTXTYTZT为刀具坐标系,其原点OT位于刀具轴线平行于Z轴时刀具的末端尖点;ORXRYRZR为回转坐标系,原点OR为B轴和C轴回转中心线的交点。

假设如下条件:所有坐标系的方向与机床坐标系的方向一致,均为直角坐标系,遵循右手笛卡尔定则;旋转轴中心线与坐标轴平行,没有其他偏角;工件坐标系OMXMYMZM与刀具坐标系OTXTYTZT仅在Z方向上相差摆长L,X、Y、Z方向没有其他偏置;在初始位置时,刀具轴线平行于Z轴。按照图2所示的运动链,OT在工件坐标系OMXMYMZM中的位置可用向量PM[PMX,PMX,PMX]表示,OR在刀具坐标系OTXTYTZT的位置可用向量MT[0,0,L]表示。刀具绕B轴、C轴旋转,引起的坐标变换可表示为[9]:
(1)
刀尖点在回转坐标系ORXRYRZR内的初始位置,可用向量TL[0,0,-L]表示。当刀轴方向发生变化时,刀尖点在工件坐标系内的位置变化量,可由向量TL在回转坐标系ORXRYRZR内的旋转与坐标系ORXRYRZR相对于OTXTYTZT的平移得到。刀具旋转后,在工件坐标系中引起的位置变化量可表示为
ΔP=RB·RC·TL+MT。
(2)
RTCP的核心在于刀具摆动角度时,仍然能够保持刀尖点在工件坐标系内的位置不变。因此,在工件坐标系内,为保持刀尖点位置不变,刀具旋转后的线性轴坐标P[PX,PY,PZ]可由原工件坐标减去刀具位置变化量获得:
P=PM-RB·RC·TL-MT。
(3)
将PM、RB、RC、MT、带入式(3),可得
(4)
串联机械机器人、并联机器人、五轴联动数控机床RTCP本质上都属于笛卡尔坐标系的坐标变换问题,可采用运动学正逆解来实现位置计算。对于B-C结构砂型五轴联动RTCP成形,运动学逆解是以主轴末端的刀尖点位置即编程坐标作为输入,逆向计算出各电机位置。运动学正解是以各电机位置作为输入,经过B轴、C轴旋转变换,计算主轴末端的刀尖点位置。控制器按照设定的周期,循环调用正、逆解程序,不断刷新指令位置,实现编程坐标的调用和各电机位置RTCP逆解计算。式(4)为逆向运动学公式,正向运动学公式可由式(4)变换得到:
(5)
将B-C双摆头RTCP正逆解公式即式(4)和式(5),分别封装到PMAC中,控制器会在运动过程中读取编程坐标,自动调用逆向运动学RTCP算法,实时进行线性轴运动轨迹及插补计算,实现五轴联动加工。
2 砂型五轴联动高速成形速度前瞻控制
2.1 砂型五轴联动成形速度波动分析
五轴联动加工过程中,由于数据量庞大,控制系统往往无法提前进行大量的RTCP逆解运算,运动速度只能根据编程坐标计算。基于该原理,采用五轴矢量速度控制时,每组指令点间的时间间隔t可根据编程坐标与编程速度的比值计算:
t=
(6)
式中:F为编程速度;μX、μY、μZ、μB、μC为长度或角度的标准单位转换为脉冲值的数量值。
在没有受到限制的情况下,各轴进给速度可由RTCP逆解位置增量除以时间间隔得到
(7)
五轴联动加工矢量速度是各轴速度的矢量和,可得
Fact=F×
(8)
由上述可知,五轴联动加工过程中,各轴实际运行的是RTCP逆解位置,而运动时间却是根据正解位置确定的,从而导致线性轴速度大幅超过编程速度,甚至超过最大速度限制。对于双摆头结构砂型五轴联动高速成形,当刀具长度较长时,线性轴实际速度超过编程速度幅度尤为明显。砂型五轴高速成形过程中,线性轴速度过高,会引起设备振动和报警,砂型材质易碎,极易造成砂型成形缺陷,损坏砂型。
2.2 砂型五轴联动高速成形单轴前瞻控制策略
为将砂型五轴联动高速成形过程中的各轴速度限制在允许范围内,采用前瞻控制是一种有效的方法。由式(7)可知,X轴、Y轴速度比如下:
(9)
由式(9)可知,五轴联动加工过程中,可以规划加工速度曲线,但各轴速度比值始终受到位置变化率比值的约束。同理,其他各轴速度间也存在位置变化比例约束关系。因此,可以通过前瞻控制限制任一坐标轴的速度,实现其余4个坐标轴的速度控制,避免进行的5个坐标轴的在线前瞻计算。当各轴存在正、负速度限制时,由式(7)和式(9),得到VX约束范围如下
(10)
根据式(10),可得到X轴的速度范围,边界值称为X轴前瞻速度阈值,用VXthreshold表示。将X轴最大速度设置成前瞻速度阈值,就可通过X轴单轴速度前瞻控制,实现五轴联动速度整体控制。同理可得,由Y轴、Z轴、B轴、C轴作为单轴前瞻控制轴时,速度范围计算公式如式(11)~式(14)所示,同样可以将获得的最小速度边界值作为单轴前瞻控制时的速度阈值。
(11)
(12)
(13)
(14)
砂型五轴联动高速成形前瞻动态控制原理图如图3所示。计算机数字控制(Computer Numerical Control, CNC)系统从加工文件中循环读取加工坐标,获得刀尖点位置。根据PMAC系统前瞻控制机理[13],计算前瞻运行所需的时间段数,并设置该轴速度最大值及前瞻运行缓存区,用于存放历史数据和前瞻计算数据;从X、Y、Z、B、C五个坐标轴中选取一个坐标轴作为前瞻控制轴,设置该轴的前瞻速度阈值。程序运行后,执行RTCP正逆解运算,正逆解运算周期通常为1~10 ms。砂型五轴联动高速进给过程中,前瞻动态控制提前将运动拆分成小片段,按照设定的时间间隔,进行前瞻计算。如发现计算得到的RTCP逆解速度超限,将通过调整时基,规划出合适的加减速,保证加工过程稳定地进行。

参照文献[13],可按式(15)计算单轴前瞻控制所需要的时间段数:
(15)
式中:ts为前瞻伺服周期,Amax为该轴最大加速度。
3 砂型五轴联动成形实验及分析
3.1 砂型五轴联动成形计算
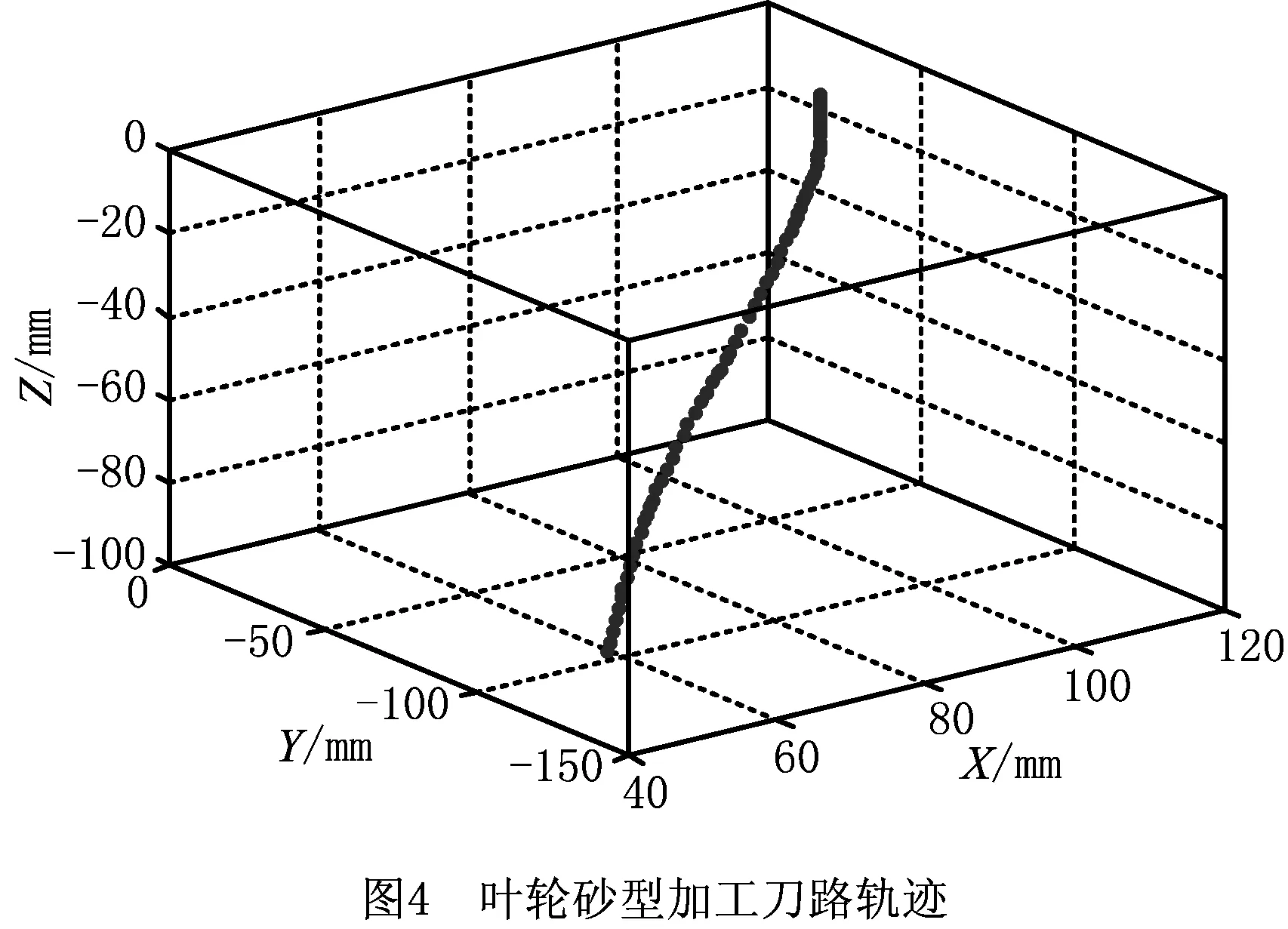
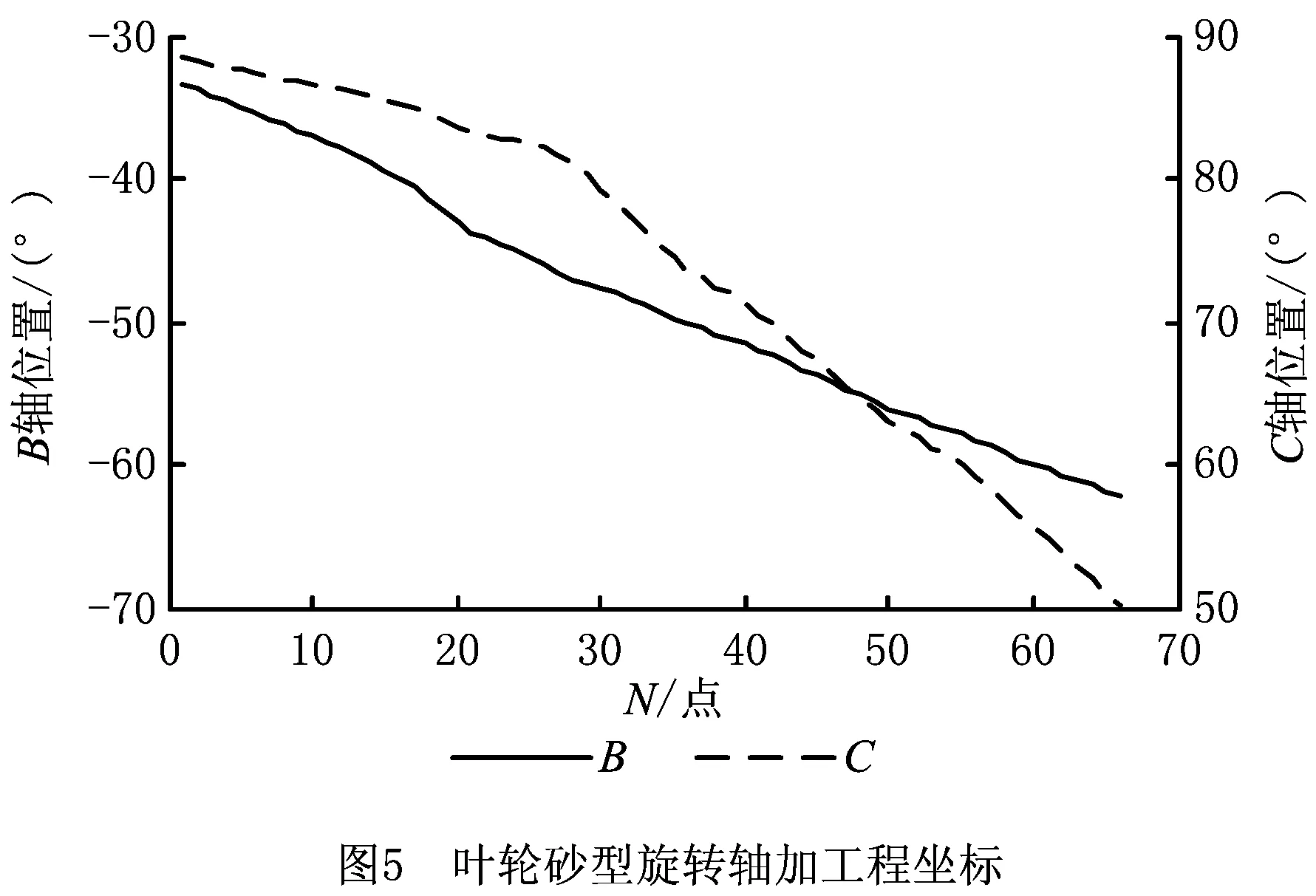
采用UG进行叶轮砂型三维建模,在CAM模块中选取自动刀轴加工模式,加工策略为从包覆圆柱插补到轮毂,坯料尺寸为337 mm×337 mm×166 mm,刀具直径为10 mm,切深恒定为6.6 mm。经过后置处理生成加工程序后,提取其中66个加工点的刀路轨迹,如图4所示,旋转轴编程坐标如图5所示。
将叶轮砂型五轴编程坐标作为RTCP正解位置坐标代入式(4),得到线性轴RTCP正逆解位置对比图,如图6所示。可以看出,与线性轴编程坐标PM相比,RTCP逆解后的位置P变化幅度较大。

按照式(6)和式(7),当计算编程速度为F500时,线性轴进给速度如图7所示,旋转轴进给速度如图8所示。


3.2 砂型五轴联动成形加工实验
本文实验设备为机械科学研究总院研制的数字化五轴无模铸造精密成形机,如图9所示。设备采用伺服电机驱动丝杠进给,控制系统为PMAC控制器。主轴采用电主轴,功率为8 KW,最高转速为12 000 rpm,刀具采用专用空心立铣刀。各进给轴参数如表1所示。


表1 数字化五轴无模铸造精密成形机进给轴参数
实测摆长L为403.70 mm,刀具直径为10 mm。设置RTCP正逆解运算周期为5 ms,编程速度为F500,矢量速度控制模式、直线插补,主轴转速6 000 rpm。启动RTCP正逆解计算,进行叶轮砂型五轴联动成形加工实验。叶轮砂型五轴联动加工过程如图10所示,成形过程平稳,砂型表面成形质量较好。

利用PMAC控制系统自带的Pmac Plot32 Pro数据采集软件,采集线性轴实际位置曲线如图11所示,图中Mtr1、Mtr3、Mtr4分别对应X、Y、Z三个线性轴,。

以X轴位置为横坐标,Y、Z轴位置为纵坐标,按照线性差值的方法,将图6中的逆解位置仿真计算与图11的实际运行进行对比,得到与控制器RTCP运行与仿真计算之间的位置误差如图12所示。
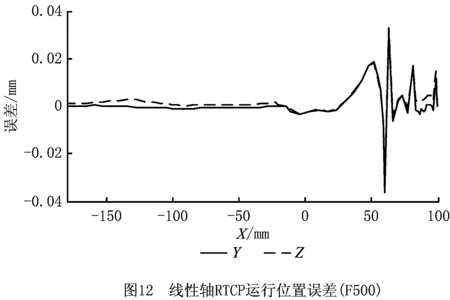
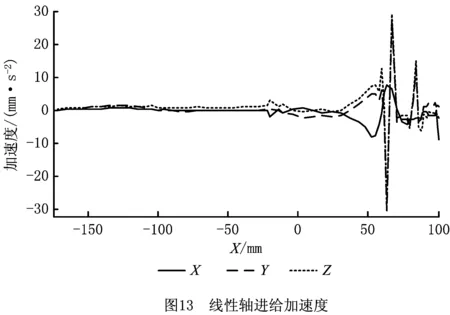
由图12可知,Y方向出现-0.036 mm误差、Z方向出现了-0.034 mm的最大误差。按照式(7)计算RTCP逆解线性轴的速度变化量,除以式(6)所示的时间间隔,得到线性轴进给加速度,如图13所示。可以看出,RTCP线性轴运行位置误差与进给加速度之间存在一定的对应关系。由于X轴进给加速度较小,Y轴、Z轴进给加速度最大时,RTCP的最大运行误差也最大。由式(4)、式(6)、式(7)可以看出,各进给轴加速度的大小及变化幅度取决于工件的轮廓特征、摆长长度及刀轴变化。此外,数据采样间隔、RTCP计算周期、各轴PID运算、反馈等环节也对误差大小产生了一定影响。
采集加工过程中线性轴速度、旋转轴速度,如图14和图15所示。其中:X轴位置作为横坐标,各轴速度作为纵坐标;Mtr5对应C轴,Mtr6对应B轴。

通过对比图7与图14、图8与图15,可知五轴实际加工速度曲线与仿真计算基本一致。在速度没有受到限制的情况下,矢量速度控制时,各轴速度变化规律可按式(7)计算。
3.3 砂型五轴联动成形高速进给实验
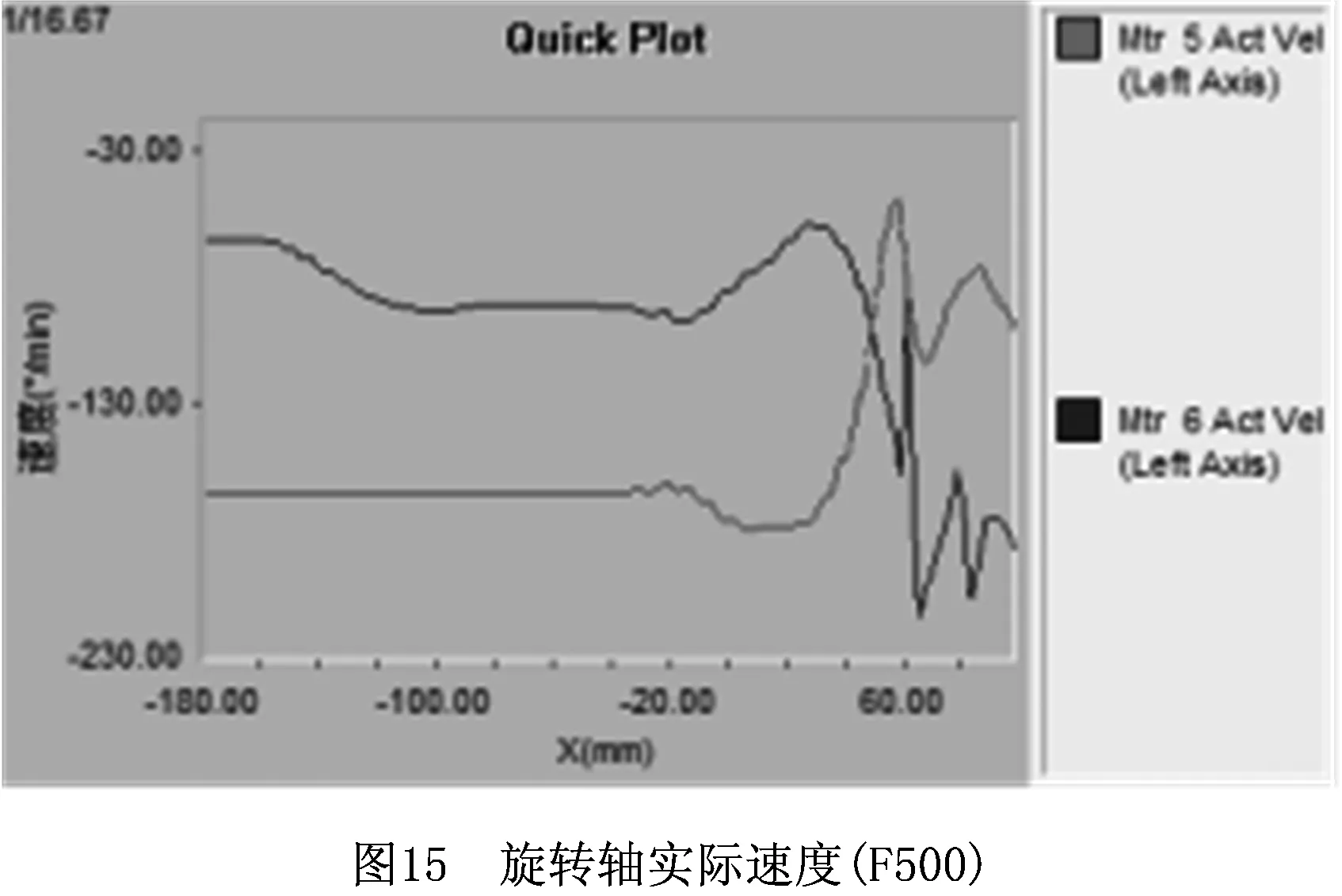
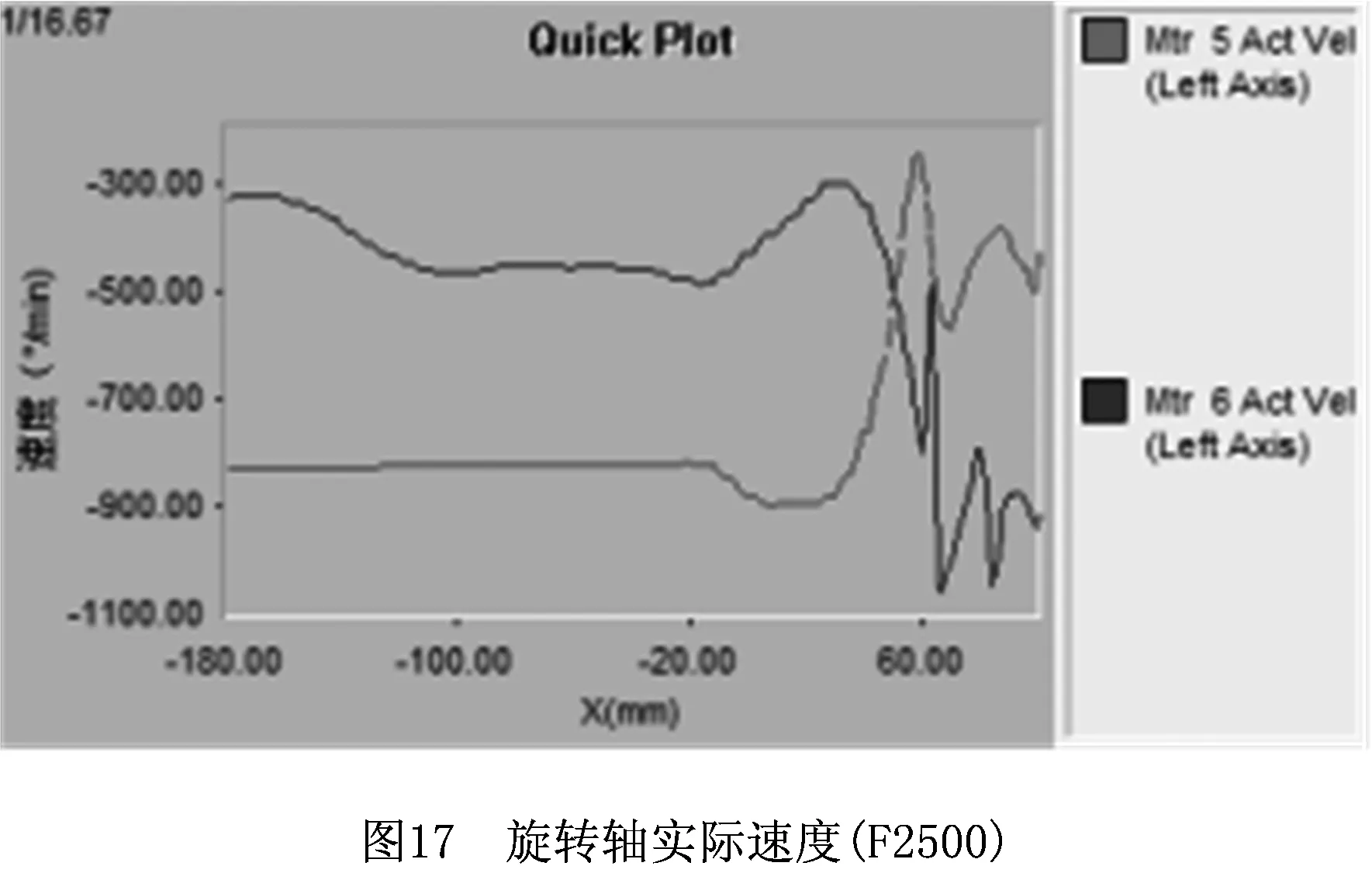
为进一步提高砂型五轴联动成形效率,在上述叶轮砂型加工程序中,设置编程矢量速度为F2500,重新运行加工程序。采集线性轴实际速度如图16所示,旋转轴实际速度如图17所示。线性轴进给速度变化较大,均大幅超过了编程速度F2500,且速度波动较大,设备出现明显振动。其中:X轴最大速度达到了-6 440 mm/min,Y轴最大速度达到了-7 528 mm/min,Z轴最大给速度达到了-6 119 mm/min。与线性轴相比,旋转轴的速度较低。可见,对于砂型五轴联动高速成形,采取前瞻控制十分必要。

同样,使用Plot32采集线性轴实际位置曲线,与RTCP仿真计算对比,得到X轴位置为横坐标时,Y轴、Z轴位置误差曲线如图18所示。

对比图12和图18,可以看出,编程速度增加到2 500 mm/min后,对应加速度进一步增加,RTCP运行位置误差也进一步加大,Y轴方向出现0.072 mm的误差,Z轴方向出现0.077 mm的误差。
3.4 砂型五轴联动高速成形前瞻控制实验及分析
选取Z轴作为前瞻控制轴,验证五轴联动速度控制效果。取各轴正向、反向速度极限值相等,分别设置各轴伺服驱动器电子齿轮比及脉冲分频,使线性轴脉冲当量为1 μm、旋转轴脉冲当量为0.001°,即μX、μY、μZ、μB、μC均为1 000。Z轴前瞻速度阈值计算公式即式(12),可进一步化简为:
(16)
取X、Y、Z三个线性轴最大速度均为2 500 mm/min,B、C轴的最大速度为1 000°/min。按式(16),计算Z轴速度限制曲线如图19所示,VZ的最小值为1 234.1 mm/min,出现在X轴速度限制曲线上。

设置Z轴的前瞻阈值VZthreshold=1 234.1 mm/min。其他各轴速度可取消限制,或设置成控制系统允许的最大值。由式(15)可知,仅Z轴的最大加速度会对前瞻计算时间段数产生影响。计算未使用前瞻控制、编程速度为F2500时,各轴最大加速度为757.3 mm/s2。设置Z最大加速度1 500 mm/s2,前瞻计算伺服周期为5 ms。按照式(15),计算得到Z轴前瞻控制时,需要提前5个周期进行前瞻运算。
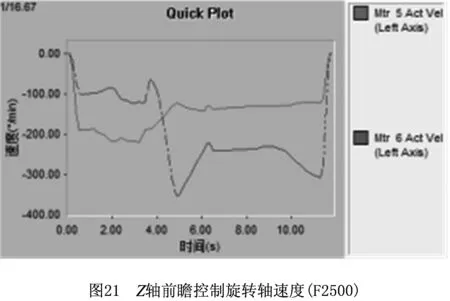
Z轴前瞻控制启动后,运行叶轮砂型加工程序,采集线性轴速度如图20所示,旋转轴的速度如图21所示。加工时长由3.31 s延长为11.4 s。可见,遇到超速状况时,前瞻控制通过提前计算来动态调整时基,虽然牺牲了响应时间,但线性轴速度超限部分得到提前计算规划,各轴速度均被限制在期望限值以内。其中X轴实际运行的最大速度最接近限制值。各轴速度波动得到明显抑制,设备运行平稳。可见,通过对Z轴单轴前瞻控制,实现了五轴联动整体速度约束控制。

按照文献[20],前瞻控制过程中,采用三次样条拟合运动学逆解离散点,所引起的误差
(17)
式中:V为前进方向的矢量速度,T为RTCP运算周期,R为运行轨迹的曲率半径。
按图7所示的叶轮砂型X轴、Y轴、Z轴RTCP逆解位置,计算运行轨迹的空间曲率半径R如图22所示。曲率半径变化幅度较大,曲率半径最大值为1 778.96 mm,最小值为10.23 mm。按照图20所示的线性轴速度,计算得到矢量速度V,如图23所示。


将RTCP运算周期5 ms、曲率半径及矢量速度带入式(17),得到叶轮砂型前瞻控制引起的误差,如图24所示,最大误差为0.000 52 mm。对比图22可知,前瞻控制引起的最大误差发生在曲率半径最小处。

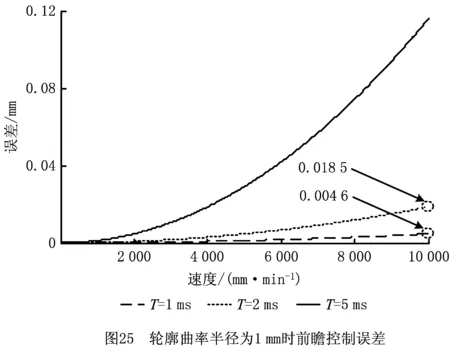
当RTCP运算周期分别为1 ms、2 ms、5 ms,曲率半径为1 mm轮廓时,在不考虑刀具的情况下,按照式(17),计算前瞻控制引起的误差如图25所示。可见,当遇到的“尖角”轮廓曲率半径较小、进给速度很高时,需要进一步缩短RTCP运算周期,以减小前瞻控制引起的轮廓误差。
文献[15]通过对五轴联动中的X、Y、Z三个线性轴进行前瞻控制,实现了五轴联动速度控制。与之相比,本文提出的前瞻控制模式,可以通过对任意1个坐标轴的速度进行前瞻控制,实现五轴联动加工整体速度控制,大大减小了前瞻控制在线计算的计算量,从而更加灵活、方便,实用性更强。
4 结束语
本文根据砂型五轴B-C双摆头结构RTCP正解、逆解运动数学模型,利用开放式控制系统高速循环调用正、逆解程序,实现编程坐标的调用和各电机位置RTCP实时计算,实验表明控制所引起的误差在砂型误差允许范围内,推导的RTCP模型和正逆解的实现方式能够实现砂型五轴联动成形。根据推导的五轴联动矢量速度计算公式,RTCP位置补偿运动是造成砂型五轴联动高速加工过程中线性轴速度波动和过冲的主要原因,各轴速度与位置变化率比值存在约束关系。五轴联动高速进给加工需要采取速度控制措施,才能保障加工过程的顺利进行。
按照本文提出的方法,可以将五轴中的任意4轴速度设置到最大,剩下1个单轴作为前瞻控制轴,通过该轴速度前瞻控制实现五轴联动加工整体速度控制,避免在线进行复杂的5个坐标轴的在线前瞻计算。单轴前瞻控制策略和前瞻阈值计算方法可以推广到其他五轴联动高速进给加工领域,具有一定的指导意义和参考价值。前瞻控制实现了五轴高速进给加工速度约束,并没有明显改善运动轨迹。为进一步提高砂型五轴联动成形效率,针对微小直线段轨迹光顺是今后的研究方向之一。

