非平稳需求面向订单装配系统库存稳定性研究

金 鑫,王正肖,叶建芳,潘晓弘

(1.浙江大学 机械工程学院，浙江 杭州 310027；2.浙江大学 华南工业技术研究院，广东 广州 510700)

0 引言

面向订单装配(Assemble to Order, ATO)是一种按照订单组织生产的生产模式。自上世纪80年代以来，对ATO生产系统的库存控制问题的研究有很多，其中库存补货策略(inventory replenishment policy)和库存分配策略(inventory allocation policy)是两个比较重要的研究问题。库存控制模型包括单周期模型、离散多周期模型和连续时间模型3种类型[1-2]。

本文研究的库存模型属于连续时间模型。在3种模型中，连续时间模型是最符合现实情形的，也是求解最困难的。对连续时间模型下ATO系统的库存控制问题有两种研究思路：①直接求解其最优库存补货策略和最优库存分配策略；②在给定的库存补货策略和库存分配策略组合下，求解最优参数和系统性能。

与本文研究相关的文献很多，这里仅简单介绍一些重要文献。Chen等[3]的研究表明Rosling[4]的结论可以从离散多周期系统推广到连续时间的情况下，即一个确定补货提前期的组装系统，在一些关于初始库存的较弱的假设下，可以等价于一个串联系统。根据Clark等[5]的经典研究结论,串联系统的最优库存补货策略是层级基准库存策略(echelon base-stock policy)。Ha[6]研究了一个具有多种需求类型和失销的单产品M/M/1队列。在最优策略下，每一种产品类型都有一个定量配给的阈值，当零部件现有库存小于等于该阈值时，系统将拒绝该类型的产品需求。De Vericourt等[7]在产品缺货的情况下研究了类似的问题，其最优策略也具有类似的形式。Lu[8]结合样本路径分析(sample-path analysis)和线性规划，给出了W型ATO系统产品成本对称时的最优策略形式以及产品成本不对称时的渐进最优策略形式。Pang[9]研究了分配系统的最优库存控制问题，利用L-convexity的概念,给出了最优库存策略结构的刻画。Nadar[10]研究了无限时段的具有产品失销(lost sales)的一般ATO系统，作者通过大量的仿真表明格相关(lattice是一个数学结构，学界通常翻译成“格”)的基准库存(lattice-dependent base-stock)策略和格相关的定量配给(lattice-dependent rationing)策略有可能是一般ATO系统的最优库存策略组合。Martin[11]将零部件补货提前期相同的ATO系统的最优化问题转化为一个两阶段随机规划问题，第一个阶段使用基准库存策略，第二个阶段使用线性规划来确定库存分配，他们证明这样的策略组合是渐进最优的。但斌等[12]研究了采用准时制生产和(r，nQ)策略的混合补货策略的ATO系统，表明了企业对何种类型的零部件采用准时制生产补货方式能够降低供应链库存成本。

Song[13]对ATO库存问题研究给出了3个关键性的结果：①提供了ATO系统的连续时间模型研究的基本框架；②证明了产品需求的时段满足率可以转化为即时满足率；③表明了即时满足率可以通过一系列的卷积迭代计算求得。Song[14]研究了相同模型下的产品缺货问题，由于产品缺货的精确计算相当复杂，该文献只给出了其上下界的表达式。Lu[15]用概率母函数法确定了在订库存联合分布、产品满足率以及缺货分布等许多重要指标的解析表达式。Lu[16]将上述方法推广到了产品需求服从更新过程、采取(r，nQ)策略的ATO系统中，同时还研究了产品需求和补货提前期的波动性变化对系统性能的影响。Zhao等[17]研究了基准库存策略和先到先得(First Come First Served, FCFS)策略下，产品需求为独立的齐次泊松过程、零部件补货提前期为序贯随机变量时，组装系统的产品满足率的精确表达式和一般ATO系统的一些重要性质。

Hoe等[18]研究了产品需求服从齐次泊松过程、零部件补货提前期是确定值的一般ATO系统的订单满足率的近似表达式。当零部件生产设备的能力有约束时，Song等[19]给出了基准库存策略和FCFS策略下，产品需求为泊松过程、单个生产设备且生产时间服从指数分布时，一般ATO系统的产品需求满足率的精确表达式。Cheung等[20]考虑了产品需求是多变量泊松过程时的情况，利用Jensen不等式给出了产品缺货期望的一个近似表达式。

在现实中，由于某些外生变量的影响，产品需求的到来强度可能是时间的函数(在最常见的情况下，产品需求存在“淡季”和“旺季”)。比如，假设某实施ATO生产模式的企业的各产品需求呈现周期性波动，且：①不同产品的需求波动性大小不同；②不同产品的需求波动周期性不同，有些产品的波动周期是一个月，有些产品的波动周期是一个季度等；③不同产品的需求波动之间相关性不同，有些产品间的需求波动是“正相关”的，有些产品的需求波动是“负相关”的。而通用零部件的存在，使得上述波动性在零部件层面产生了叠加，进一步增加了库存控制的复杂性。显然，此时ATO系统的零部件库存控制策略的最优参数值与(复合)齐次泊松过程情况下会有很大不同。因此，需要研究产品的需求到来强度存在波动时ATO系统的各种重要性能指标的求解，以及需求到来强度的波动对系统性能的影响。本文通过将产品需求到来过程建模为带时倚强度的泊松过程，对上述问题给出了部分解答。

1 模型的基本概念及基础假设

(1)装配物料清单结构

(2)各项成本

在任何时刻，零部件i导致的库存持有成本与其现有库存(stock on hand)成正比，产品j导致的缺货成本与其缺货成正比。零部件i的单个现有库存的单位时间库存持有成本为hi，产品j的单个缺货的单位时间缺货成本为bj。

(3)库存控制策略

ATO系统中的库存控制策略包括库存补货策略和库存分配策略。

在本文的证明部分中，采用基准库存策略(base stock policy)来管理零部件的库存补货，其中零部件i相应的控制参数为si。当零部件i的库存位置(IP)小于si时，立即触发一个对其的补货，使得其库存位置重新回到si。

库存分配策略为“先到先得”(First Come First Served, FCFS)策略，即:①当一个产品的需求到来时，若此时相应零部件的库存水平(IL)大于等于该产品对其所需个数，则该需求被立即满足，否则就进入缺货队列中等待；②当零部件的补货到来时，产品的缺货按照其相应需求到来的时间先后顺序进行满足；③当一个产品的需求到来时，若其相应的零部件需求只有部分得到满足，则将这部分的零部件库存“绑定”给该产品的需求。此后，其他产品需求将不能使用这些零部件库存。

(4)系统状态变量

H(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的现有库存的分布，H(t|s)=[H1(t|s),H2(t|s),…,Hm(t|s)]T；

B(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的产品缺货的分布，B(t|s)=[B1(t|s),B2(t|s),…,Bn(t|s)]T；

O(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的在订库存的分布，O(t|s)=[O1(t|s),O2(t|s),…,Om(t|s)]T；

IL(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的库存水平的分布，IL(t|s)=[IL1(t|s),IL2(t|s),…,ILm(t|s)]T；

IP(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的库存位置的分布，IP(t|s)=[IP1(t|s),IP2(t|s),…,IPm(t|s)]T；

c(t|s)为在给定结构以及库存控制参数下的ATO系统在时刻t的单位时间系统库存总成本。

(5)零部件的补货提前期和产品需求到来过程

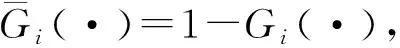
由于产品需求的到来过程是带时倚强度的泊松过程，只具有独立增量性而一般不具有平稳增量性，从而导致相应的ATO系统不一定会有平稳状态。因此，对于任意一个和时间有关的系统状态，转而研究它的平均分布，如平均在订库存分布、平均缺货分布、平均时段满足率分布等。

2 ATO系统的关键性能指标与初步结论

ATO系统的关键性能指标包括时段满足率、等待时间、缺货队列长度和总库存成本。

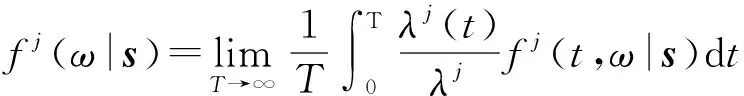
根据系统总库存成本的定义，在时刻t有：

c(t|s)=hH(t|s)+bB(t|s)；

(1)

根据各系统状态变量的定义，在时刻t有：

IP(t|s)=IL(t|s)+O(t|s)

=H(t|s)-AB(t|s)+O(t|s)；

(2)

根据基准库存策略的定义，在时刻t有：

IP(t|s)≡s。

(3)

联合式(1)～式(3)，可以得到：

c(t|s)=hs+(hA+b)B(t|s)-hO(t|s)。

(4)

对式(4)的两端在无限时间段内求平均，可以得到ATO系统的平均总库存成本期望的表达式：

(5)

进一步分析之前，易看出各性能指标满足如下两个性质：

(1)根据Endou[22]中关于Fubini’s定理成立的前提条件易知，当上述表达式中出现多个积分时，积分顺序可以交换。

(2)当其他条件相同时，对于不同初始状态的ATO系统，它们对应的平均性能指标将随时间t依概率收敛到同一分布。因此，ATO系统的平均总库存成本期望与初始状态无关。

3 ATO系统的在订库存分布及产品缺货分布

由平均单位时间总库存成本的表达式可知，求解它的关键在于获得任一时刻t的在订库存分布及产品缺货分布。下面先获得ATO系统在订库存分布的表达式。

3.1 ATO系统的在订库存分布

对于任何一种产品，其需求导致的在订库存在时刻t的分布求解过程与单产品—单零部件的情况类似。不失一般性，任选一种产品j。设产品j在[0,t]内一共来了d个需求，即Dj[0,t]=d。根据单产品—单零部件的类似求解过程，可以得到，当Dj[0,t]=d时，

(6)

因此，在时刻t产品j导致的在订库存分布的概率母函数为：

u)+Gi(t-u))-1)du)。

(7)

进一步，可以得出系统在时刻t的在订库存分布的概率母函数为：

Gi(t-u))-1)du)。

(8)

时刻t零部件i的在订库存的期望为：

(9)

零部件i的平均在订库存的期望为：

(10)

3.2 产品平均缺货分布及其期望

在一般ATO中，无法由在订库存的分布信息直接求出各产品的缺货分布。通常的做法是先求出每个产品的时段满足率，进而求出其期望等待时间，最后利用Little’s Law[21]求出每个产品的缺货期望。详细求解过程如下。

不失一般性，任选一类产品j，设在时刻t到来了一个产品j的需求，下面首先求出该需求的时段满足率。

因为使用FCFS策略进行库存分配，所以产品j的需求的时段满足率为P{Wj(t|s)≤ω}=P{si-Oi(t+ω|s)+Di(t,t+ω]≥0,i∈Kj}。显然，Oi(t+ω|s)包含Yi,1(t+ω|s)、Yi,2(t+ω|s)和Yi,3(t+ω|s)三部分，它们分别表示时刻t之前到来的需求所触发的补货、时刻t到来的产品j的需求所触发的补货、(t,t+ω]之间到来的需求所触发的补货在时刻t+ω时还有多少仍然在订。因此，时段满足率可以表示为：

P{Wj(t|s)≤ω}=P{Oi(t+ω|s)-

Di(t,t+ω]≤si,i∈Kj}

=P{Yi,1(t+ω|s)+Yi,2(t+ω|s)-

(Di(t,t+ω]-Yi,3(t+ω|s))≤si,i∈Kj}。

(11)

根据上式，可求出在随机变量D[0,t)和D(t,t+ω]发生的条件下，随机变量O(t+ω|s)-D(t,t+ω]发生的条件概率所对应的概率母函数，进而根据泊松分布的概率母函数的性质可以求出φO(t+ω|s)-D(t,t+ω](z1,z2,…,zm)，详细推导过程可见Lu[15]。φO(t+ω|s)-D(t,t+ω](z1,z2,…,zm)的表达式为：

(12)

4 需求强度的周期性波动对系统平均总库存成本期望的影响

本章研究需求强度的周期性波动对于以平均总库存成本期望为代表的ATO系统性能的影响。由于求解过程较为复杂，在进行研究时，均以几个典型的库存系统为例。

考虑任意两个产品的BOM之间的关系。对于产品j1和产品j2，提出以下两个参数：①结构竞争性参数，其定义为η(j1,j2)=|{i|i∈Kj1∩Kj2,i=1,2,…,m}|；②结构互补性参数，其定义为γ(j1,j2)=|{j|Kj∩Kj1≠∅,Kj∩Kj2≠∅,Kj∩Kj1∩Kj2=∅,j=1,2,…,n}|。直观上看，结构竞争性参数表示两个产品之间通用零部件的个数，而结构互补性参数则表示分别与两个产品都具有通用零部件(但3个产品不同时具有通用零部件)的产品的个数。当两个产品的结构竞争性(互补性)参数不为0时，称它们的结构之间具有竞争性(互补性)。

分别用两个例子来表明存在结构竞争性和存在结构互补性的情况下，需求强度波动性变化的联合模式对系统性能的影响。

(1)结构竞争性

考虑一个两产品的分配系统，显然产品1和产品2的结构竞争性参数η(1,2)=1，结构互补性参数γ(1,2)=0。即产品1和产品2的结构之间只具有竞争性。

产品1的需求到来是一个带时倚强度的泊松过程，当2rQ≤t<(2r+1)Q时，其强度λ(t)=λ-ε；当(2r+1)Q≤t<2(r+1)Q时，λ(t)=λ+ε，其中r=0,1,2,…，0≤ε≤λ。产品2的需求到来也是一个带时倚强度的泊松过程，其强度分为两种情况：①模式一，当2rQ≤t<(2r+1)Q时，λ(t)=λ-ε；当(2r+1)Q≤t<2(r+1)Q时，λ(t)=λ+ε；②模式二，当2rQ≤t<(2r+1)Q时，λ(t)=λ+ε；当(2r+1)Q≤t<2(r+1)Q时，λ(t)=λ-ε，其中r=0,1,2,…，0≤ε≤λ(即ε的值在模式一和模式二中正好相反，因此在模式一和模式二中产品2的需求强度变化的波动性相同。这样设定的原因是为了控制需求强度变化的波动性对系统性能的影响)。可见，当产品2的需求到来过程满足模式一时，产品1和产品2的需求周期性强度变化是“正相关”的，而当产品2的需求到来满足模式二时，产品1和产品2的需求周期性强度变化是“负相关”的。通过比较这两种情况下系统的平均总库存成本期望的大小，来研究具有结构竞争性的两产品的需求强度波动性变化的联合模式对系统性能的影响。每个零部件的平均在订库存的期望与ε无关，根据其表达式可知，平均总库存成本期望的大小只与产品平均缺货的期望有关。

根据上述分析，有如下命题。

定理1在产品的结构之间只存在竞争性的条件下，需求周期性强度变化“正相关”时的系统的平均总库存成本的期望大于需求周期性强度变化“负相关”时的系统的平均总库存成本的期望。

证明见附录。

(2)结构互补性

产品1和产品2的需求到来过程的模式与结构竞争性情况下类似(这样设定同样是为了控制需求强度变化的波动性对系统性能的影响)，产品3的需求到来是一个强度为μ的齐次泊松过程。与之前类似，平均总库存成本期望的大小只与产品平均缺货的期望有关，且产品1和产品2的平均缺货期望保持不变，只需考虑产品3的平均缺货期望即可。

根据上述分析，有如下定理。

定理2当产品的结构之间只存在互补性时，需求强度变化“正相关”时的系统的平均总库存成本期望小于需求强度变化“负相关”时的系统的平均总库存成本期望。

证明见附录。

由定理1和定理2可知，要确定需求强度波动性变化的联合模式对系统性能的影响，需要同时考察波动性产品的BOM之间的关系和需求强度变化的相关性这两个因素。

5 需求强度波动性变化对产品缺货期望影响的仿真研究

根据前面的证明过程，设计仿真实验，研究两个问题：①不同的零部件库存补货策略下，单产品需求强度波动性变化对产品缺货期望的影响；②多产品需求强度波动性变化的联合模式对产品缺货期望的影响。

齐次泊松过程的点间间距是相互独立的指数分布，本文研究的产品需求到来是带时倚强度的泊松过程，此时需要利用其点间间距的计算公式(参见文献[23])确定产品需求到来的时间点，其余部分与通常的库存系统仿真相同。

对于问题①，构建一个由2种产品和3种零部件组成的W型ATO系统，其中产品P1由一个零部件C1和一个零部件C2装配而成，产品P2由一个零部件C2和一个零部件C3装配而成。产品P1的需求到来过程是一个强度周期性波动的带时倚强度的泊松过程，产品P2的需求到来过程是一个齐次泊松过程。设定模型参数，零部件的相关参数和产品的相关参数分别如表1和表2所示。其中，r和Q分别是(r，Q)策略中的控制参数，W为需求到来强度的波动周期。

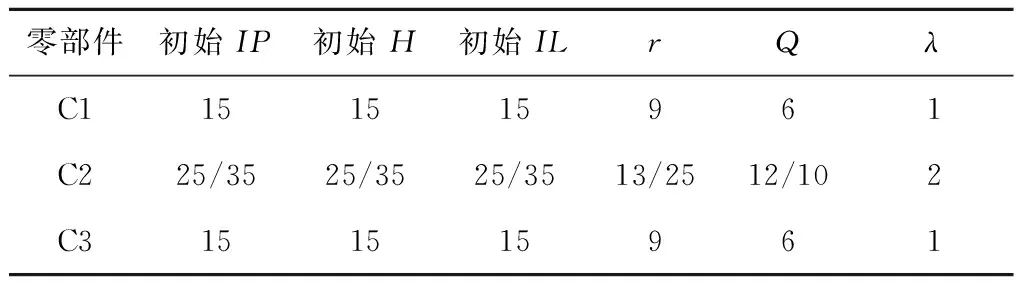
表1 仿真模型中零部件的相关参数

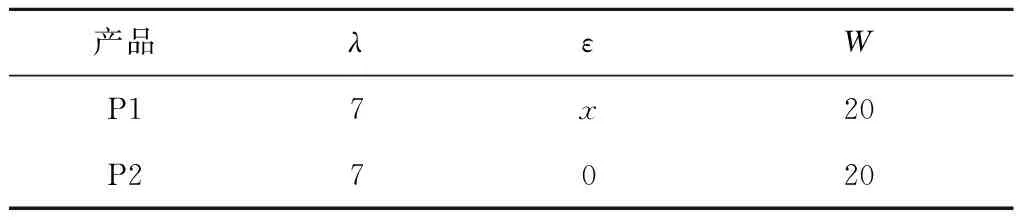
表2 仿真模型中产品的相关参数

对上述ATO系统中采用FCFS策略进行库存分配。通用零部件C2的补货策略有两种：再订货点为13，订货批量为12，此时表示通用零部件C2的库存较“稀缺”；再订货点为25，订货批量为10，此时表示通用零部件C2的库存较“充足”。产品P2的需求强度波动幅度的值为x。实验研究在零部件C2的不同补货策略下，当x变化时，产品P1和产品P2的缺货期望。对于每一次实验，仿真总时间设定为70 000单位仿真钟时间。设定仿真钟时间前20 000为初始阶段，对20 000～70 000时间内的运行数据进行统计。产品P2的需求强度波动幅度x在0～6之间每隔1取一个值。在每一次取值下，进行50次仿真。仿真结果如表3和表4所示。将表3和表4中不同补货策略下需求波动对产品缺货期望的影响绘制折线图，如图1和图2所示。所有仿真中，p值均小于0.000 1。

表3 通用零部件库存“稀缺”时的需求波动对产品缺货期望的影响

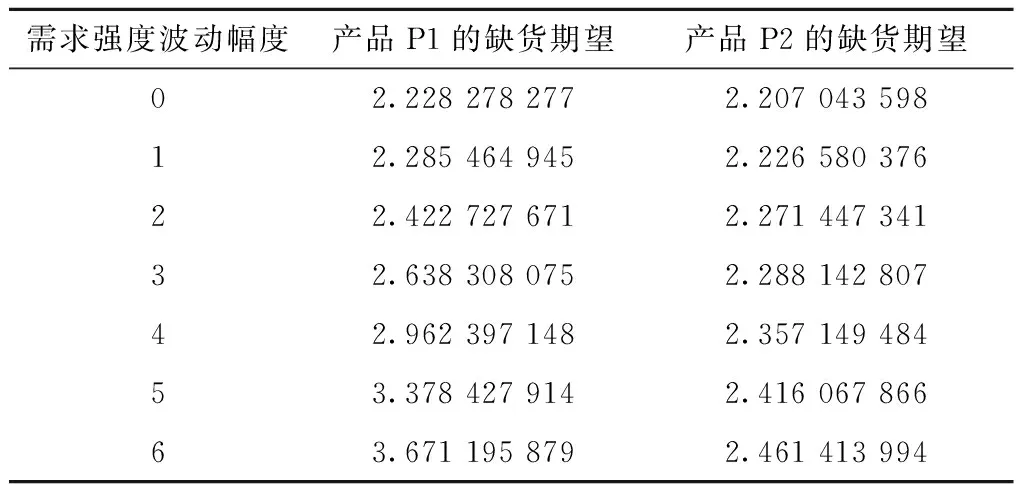
表4 通用零部件库存“充足”时的需求波动对产品缺货期望的影响

由图1和图2可以看出，对于需求具有时倚强度的产品P1，无论通用零部件库存“稀缺”还是“充足”，当需求强度波动幅度增大时，其缺货期望也增大。对于需求为齐次泊松过程的产品P2，通用零部件库存“稀缺”时，当需求强度波动幅度增大，其缺货期望先增大后减小，通用零部件库存“充足”时，当需求强度波动幅度增大，其缺货期望也增大。因此，与粗糙的直观想法相反，当通用零部件较库存“稀缺”时，产品需求的波动性增大有可能会降低ATO系统的单位时间库存总成本。

对于问题2，构建一个由3种产品和3种零部件组成的ATO系统，其中产品P1由一个零部件C1和一个零部件C2装配而成，产品P2由一个零部件C2和一个零部件C3装配而成，产品P3由一个零部件C1和一个零部件C3装配而成。可见，产品P1、产品P2和产品P3之间同时具有结构竞争性和结构互补性。设定模型参数，零部件的相关参数和产品的相关参数分别如表5和表6所示。表中各参数的意义与表3、表4相同。

表5 仿真模型中零部件的相关参数

表6 仿真模型中产品的相关参数

对上述ATO系统采用FCFS策略进行库存分配。产品P2的需求强度波动幅度的值为x。实验研究当x变化时，产品P1、产品P2和产品P3的缺货期望。对于每一次实验，仿真总时间设定为70 000单位仿真钟时间。设定仿真钟时间前20 000为初始阶段，对20 000～70 000时间内的运行数据进行统计。产品P2的需求强度波动幅度x在-6～6之间每隔2取一个值。在每一次取值下，进行50次仿真。仿真结果如表7所示。将表7中需求波动对产品缺货期望的影响绘制折线图，如图3所示。所有仿真中，p值均小于0.0001。

表7 需求波动的联合模式对产品缺货期望的影响

由图3可知，当产品P2需求强度波动幅度由负变正时：①产品P1的缺货期望增大，即影响其缺货期望的主要因素是产品P1和P2间的结构竞争性；②产品P3的缺货期望减小，即影响其缺货期望的主要因素是产品P3和P1间的结构竞争性；③产品P2的缺货期望先减小后增大，即影响其缺货期望的主要因素先是产品P2和P3间的结构竞争性，而后是产品P2和P1间的结构竞争性。因此，当多个产品均存在需求强度波动时，需要根据产品间的BOM结构关系来分析需求强度波动性变化对各产品的影响。

6 结束语

本文研究了产品需求到来强度有波动性的ATO系统，主要包括以下内容：

(1)结合带时倚强度的泊松过程的性质，利用概率母函数，求解出了时段满足率、等待时间、缺货队列长度和总库存成本等重要性能指标的解析表达式。

(2)在(1)的基础上分析了单产品与多产品的需求波动性对系统性能的影响。通过引入结构竞争性和结构互补性的概念，证明了当产品的结构之间只存在竞争性(互补性)时，需求强度变化“正(负)相关”时的系统的平均总库存成本期望小于需求强度变化“负(正)相关”时的系统的平均总库存成本期望。

(3)通过仿真实验表明在一般BOM结构的ATO系统中，需求波动性对产品缺货期望的影响十分复杂，在单产品需求波动的情况下，需要考虑通用零部件是“稀缺”还是“充足”，在多产品波动的情况下，需要同时考察波动性产品的BOM之间的关系和需求强度变化的相关性这两个因素。

在这一领域，还有很多工作需要完成，主要包括：

(1)本文中所有公式推导以及仿真研究都是在假设库存分配策略是FCFS策略下进行的，更进一步需要研究不同库存分配策略(如“先准备好先得”(First Ready First Served，FRFS)策略、定量配给策略等)下需求波动性对系统性能的影响规律。在这些库存分配策略下，系统状态之间的相关性通常更强，因此需求波动性对系统性能的影响规律预期会更加复杂。

(2)本文研究了给定库存补货参数下需求波动性对系统性能的影响，今后需要研究需求波动性对最优库存补货参数及系统最优性能的影响规律。