负泊松比梯度蜂窝结构研究

刘宇，郝琪，田钰楠，崔宏伟

（湖北汽车工业学院 汽车工程学院，湖北 十堰442002）

功能梯度材料是非均匀材料，其性能或组成结构沿长度或厚度方向成梯度分布，使结构的不同部位在不同荷载形式下充分发挥各自的功能，并且确保结构的整体性和可靠性，在抗冲击、能量吸收等方面具有一定的优越性，受到广泛关注。功能梯度多孔材料在受到面内冲击作用时，其动态响应和变形模式会随着梯度的变化而在局部发生变化。与传统材料相比，具有负泊松比效应的拉胀材料在受到拉伸时会发生侧向膨胀，这种反常的“拉胀”行为使负泊松比蜂窝材料具有更高的抗冲击、抗剪、能量吸收能力［1-4］。负泊松比蜂窝材料和功能梯度蜂窝材料在结构防护方面具有良好的应用前景。张新春等［5-6］根据功能梯度材料的概念构造了具有密度梯度的蜂窝材料模型，根据蜂窝单元细胞的几何尺寸来调整蜂窝材料的密度梯度分布，从而控制材料的能量吸收能力。姚兆楠［7-8］研究了角度梯度型六边形和内凹六边形蜂窝材料在不同冲击速度下的变形模式、应力应变曲线和能量吸收效果，分别与相应的均匀蜂窝材料进行对比，分析了角度梯度型蜂窝材料的动力学特性。

文中以某弧边负泊松比结构为研究对象，通过建立数值仿真模型，探讨该弧边负泊松比蜂窝结构和其功能梯度蜂窝结构的动力学特性，针对该弧边负泊松比结构的胞元弧夹角、内厚度、高度3 个几何参数［9］，建立3种梯度蜂窝结构，从变形模式、吸能量、比吸能及碰撞力方面对比研究均匀蜂窝结构与梯度蜂窝结构的差异。

1 角度梯度蜂窝结构

1.1 仿真设置

文中所研究弧边负泊松比胞元如图1所示，相邻胞元通过杆连接，h为胞元高，T为内部杆厚度，θ为两侧弧边切线与相临边的夹角。针对上述3 个参数建立正反梯度模型，并与均匀蜂窝结构进行对比，文中所有结构模型整体尺寸皆保持一致。

图1 负泊松比胞元结构图

采用刚性板对蜂窝结构进行冲击仿真［10］，刚性墙赋予500 kg 质量，使用MAT20 号材料卡片进行模拟，蜂窝结构使用Q235 号材料，采用MAT24号材料卡片进行模拟，壳单元类型取shell 163壳单元，使用面内单点积分，单元算法采用Belytschko-Tsay。为保证数值结果的收敛性，沿单元厚度取5个积分点。刚性墙与蜂窝结构使用面面接触，模型整体采用自动单面接触形式，忽略摩擦力的影响，约束蜂窝结构z方向移动与转动自由度，根据汽车碰撞应用场景，按照C-NCAP正面碰撞试验法规设置冲击速度为50 km·h-1，采用Ls-dyna求解器进行冲击计算［11］。

图2为均匀蜂窝结构，h为35 mm，T为1 mm，θ为50°。图3为角度梯度蜂窝结构，以3行结构为1个区域，正梯度从上至下每区域夹角依次为10°、30°、50°、70°，负梯度模型反之。

图2 均匀蜂窝结构

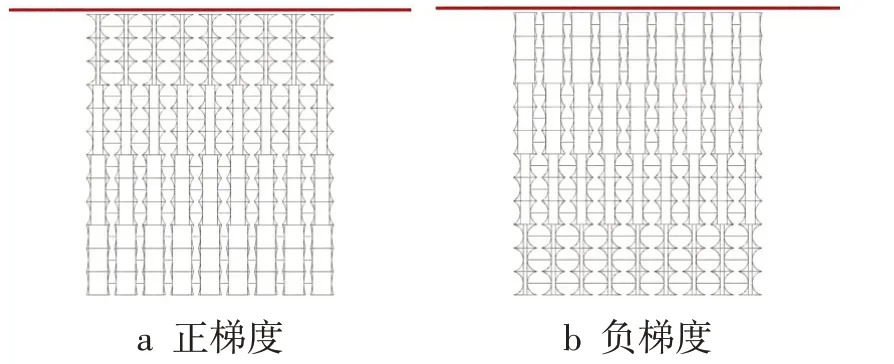
图3 角度梯度蜂窝结构

1.2 仿真研究

图4为均匀蜂窝结构不同应变下的变形模式，在应变为0.36时蜂窝结构呈现出X型变形特征，这是典型的负泊松比结构变形特性，冲击端结构首先发生收缩，随着结构继续变形，X 上部结构充分发生变形，此时呈现出倒V 型变形特征，冲击后期结构横向收缩达到极限，结构整体密度增大，负泊松比双向收缩特性达到极限。

如图5所示，角度正梯度蜂窝结构冲击端夹角较小，胞元首先发生变形且较快达到变形极限，此时蜂窝结构呈现出倒U型变形特性，变形由冲击端向支撑端两侧结构传递，最终被完全压溃。如图6所示，角度负梯度蜂窝结构冲击端胞元夹角较大，胞元近似正方形结构，在受到冲击后几乎不呈现出负泊松特性，故接近冲击端结构未呈现出向内部收缩的趋势，反而向外部发生轻微扩张，而支撑端夹角较小，呈现出的负泊松比特性较强，二者间存在较为明显的界限，在完全压溃后可以明显看到冲击端横向尺寸较大，接近支撑端的中部横向尺寸较小。与均匀蜂窝结构相比，角度梯度模型的负泊松比变形特性较弱，而角度正梯度的负泊松比特性稍好于负梯度。

图4 均匀蜂窝结构变形模式

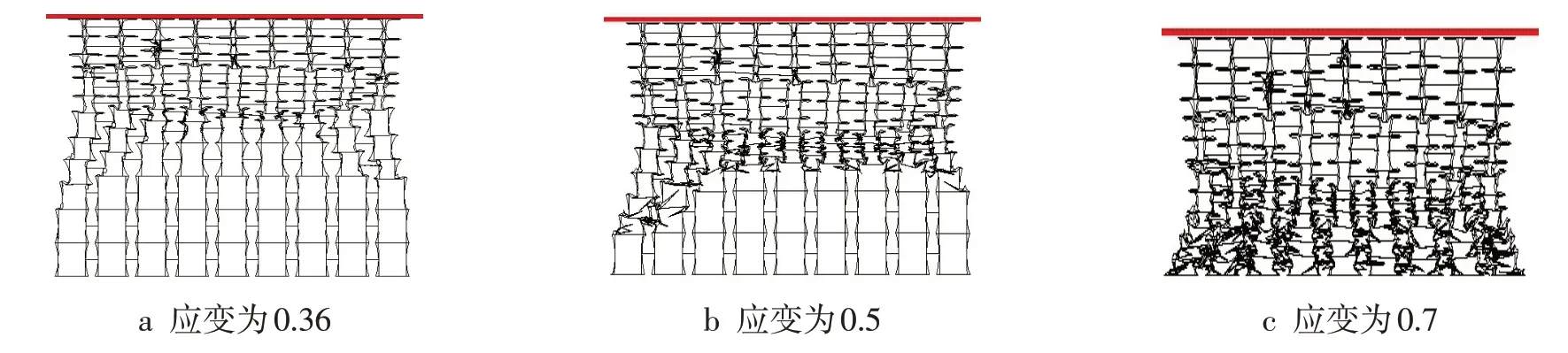
图5 角度正梯度蜂窝结构变形模式

图6 角度负梯度蜂窝结构变形模式

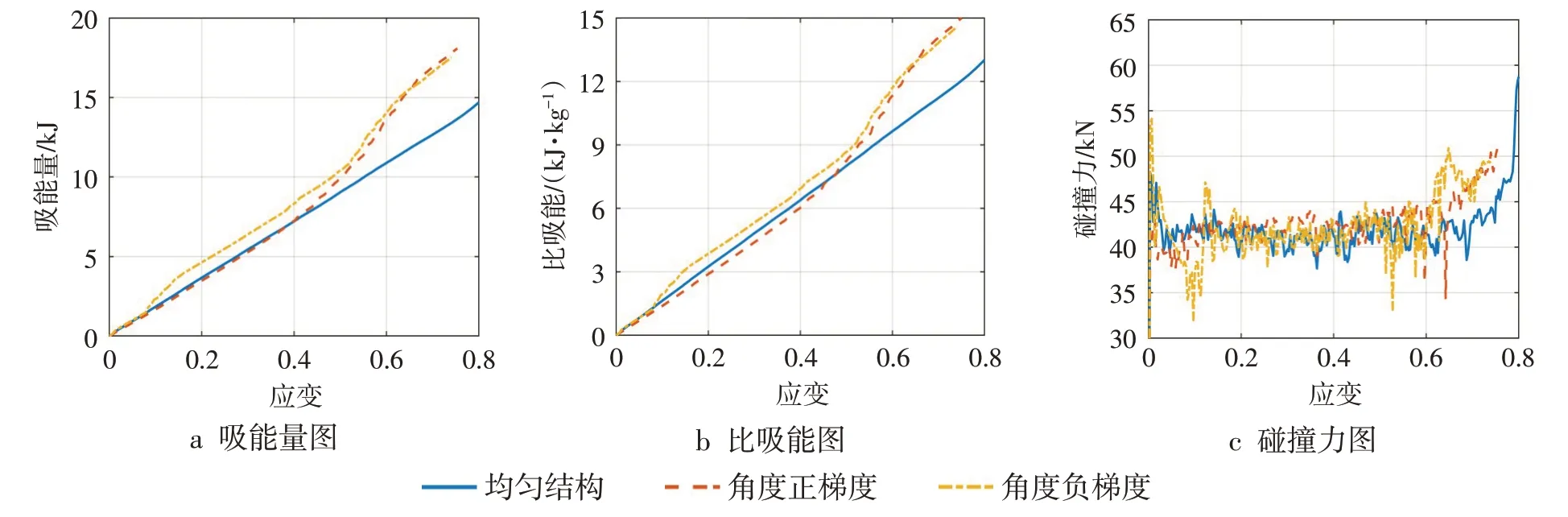
图7 角度梯度蜂窝结构数据图

吸能量和比吸能曲线如图7a～7b 所示。在冲击前期吸能量差异不大的情况下，质量影响较大，前期均匀结构略高于正梯度结构，而随着吸能量差异的增大，比吸能与吸能量变化趋势逐渐一致。吸能量曲线在冲击后期梯度模型出现了激升现象，这是由于此时夹角较大的胞元结构开始变形，从上述变形模式也可以看出夹角较大的胞元皆在后期开始受力变形，由于夹角过大，胞元近似正方形，可变形空间较大，故吸能量出现急剧上升，相应的所需变形力也较大，图7c 碰撞力曲线后期也出现了增加。在冲击开始时，角度正梯度冲击端结构夹角较小，变形诱导作用较大，极易发生变形，而负梯度与之相反，冲击端变形难度大且发生了外扩，因此角度负梯度结构第一碰撞力峰值远大于均匀结构及正梯度结构，而正梯度结构第一碰撞力峰值最小。总体上看，角度正梯度结构的吸能量及比吸能较高，负泊松比特性虽略弱于均匀结构，但第一碰撞力峰值最低。

2 内厚度梯度蜂窝结构

内厚度梯度模型整体与图2一致，正梯度内部杆的厚度从上至下依次为0.5 mm、1 mm、1.5 mm、2 mm，负梯度模型与之相反。由图8～9可以看出内厚度梯度蜂窝结构呈现出I型变形模式，即结构逐行发生压溃，结构中胞元发生双向收缩但蜂窝结构整体基本不呈现出双向收缩的负泊松比特性。结构中胞元发生变形时内厚度承担抵抗弧边变形的作用，内厚度越小胞元越容易变形，因此内厚度梯度结构中内厚度较小处首先发生变形，内厚度正梯度结构是冲击端，而负梯度结构则是支撑端。

图8 内厚度正梯度蜂窝结构变形模式

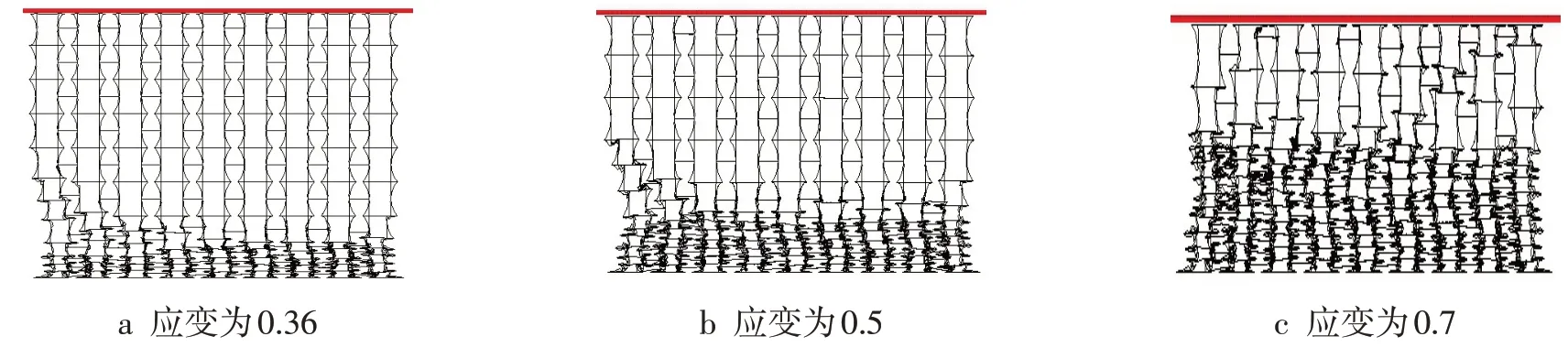
图9 内厚度负梯度蜂窝结构变形模式

内厚度梯度结构的吸能与碰撞力与角度梯度结构类似。冲击后期内厚度较大的胞元开始发生变形，由于内部杆的抵抗作用较大，胞元不易变形，达到相同纵向应变时需要更大的变形力，因此图10a～10b内厚度梯度结构吸能量后期增加较大，由于模型质量差异较小，所以比吸能变化趋势与吸能量一致。图10c 中内厚度正梯度结构在冲击开始时由于冲击端较易且首先变形，所以第一碰撞力峰值较低，而在后期需要更大的变形力使支撑端变形，后期碰撞力较大；内厚度负梯度结构冲击端不易变形，受到冲击时的冲击力从冲击端传递至支撑端，再由支撑端变形吸收，因此冲击初始的冲击端接触碰撞力较大，在后期略有降低。

图10 内厚度梯度蜂窝结构数据图

3 高度梯度蜂窝结构

图11 为高度梯度蜂窝结构，正梯度胞元高度依次为25 mm、30 mm、40 mm、45 mm，负梯度模型反之。图12为高度正梯度结构同样呈现出X型变形特征，但该效果较弱，蜂窝结构中部收缩效果较强，中部密度增加较快，完全压溃时中部横向尺寸较小。图13为高度负梯度结构从冲击端开始变形收缩，并逐步向支撑端压溃，压溃过程中虽未呈现出X型变形特性，但结构上半部整体发生向内部收缩的变形特性，完全压溃后上半部整体横向尺寸较小。高度负梯度结构完全压溃后的密度及横向尺寸与均匀结构相似，变形模式略有不同，而高度正梯度结构完全压溃后的冲击端横向尺寸略大于均匀结构与高度负梯度结构。

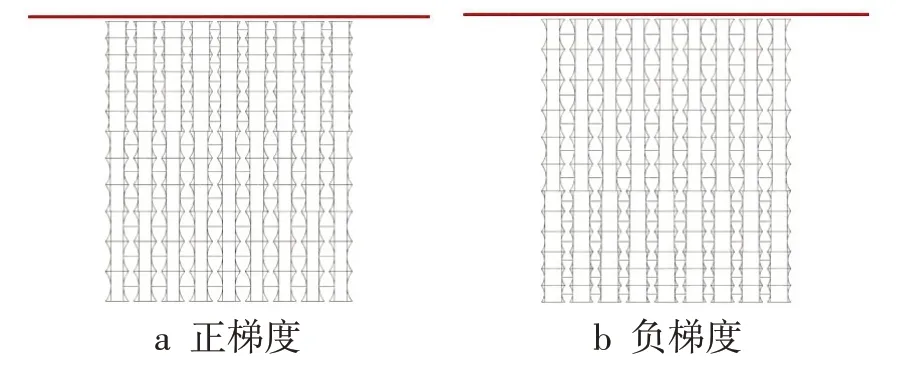
图11 高度梯度蜂窝结构

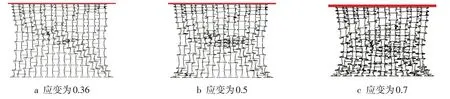
图12 高度正梯度蜂窝结构变形模式

图13 高度负梯度蜂窝结构变形模式

高度梯度蜂窝结构整体尺寸及质量与均匀蜂窝结构一致，因此不需考虑比吸能。由图14a可知高度梯度蜂窝结构与均匀蜂窝结构吸能量基本一致，图14b 中的第一碰撞力峰值也基本无差别，后期高度梯度蜂窝结构碰撞力增加较快，此时结构逐渐被完全压溃，比均匀结构更快达到密实极限。

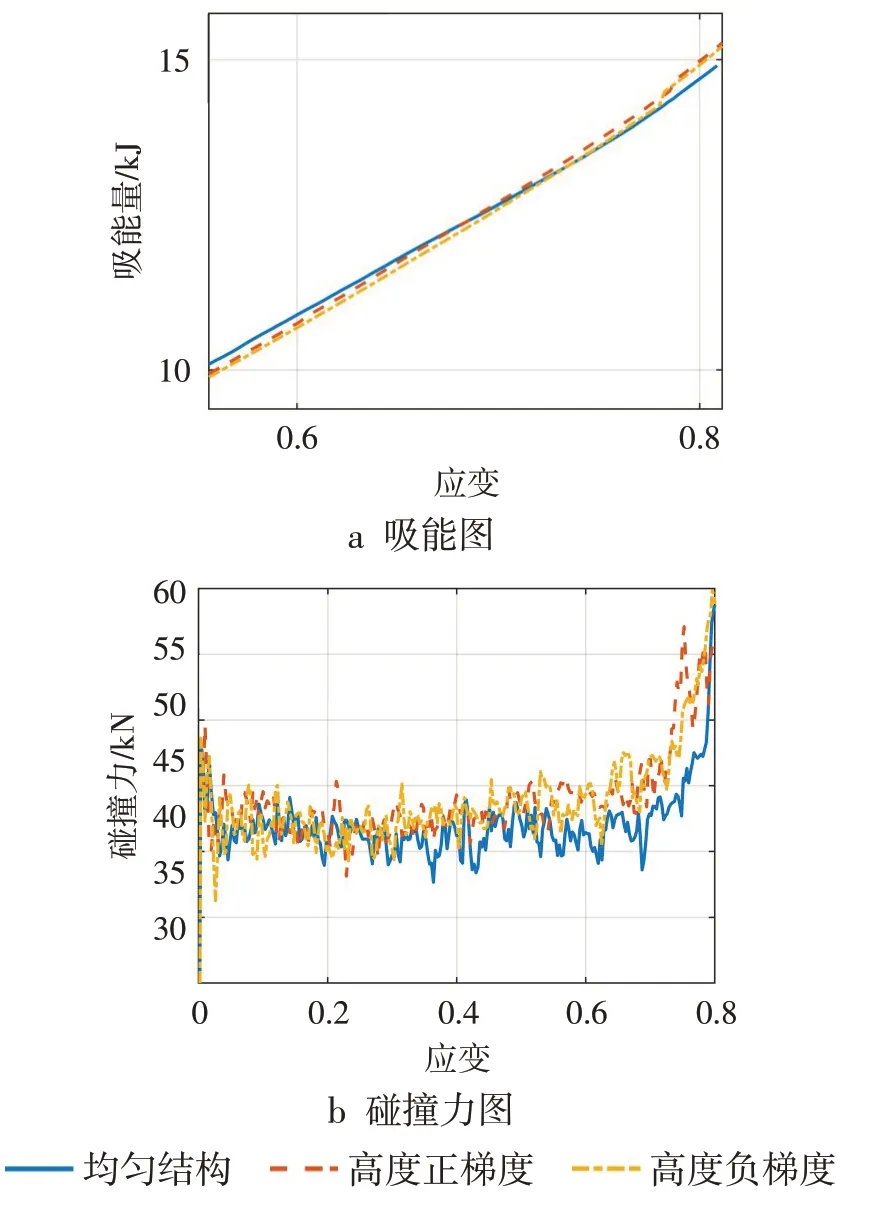
图14 高度梯度蜂窝结构数据图

纵向应变为0.7 时的各项数据如表1 所示，可以看出高度梯度蜂窝结构和均匀蜂窝结构的性能差异很小，而角度梯度结构和内厚度梯度结构的吸能量较高，由于内厚度的变化导致蜂窝结构的质量增加高于其他结构，故内厚度梯度结构比吸能低于角度梯度结构。

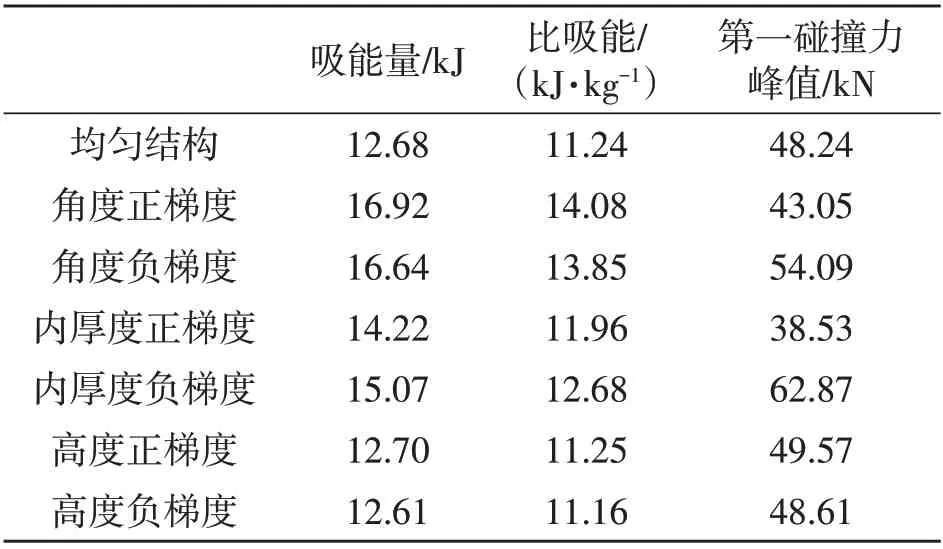
表1 等纵向应变下各梯度模型数据对比

4 结论

1）均匀蜂窝结构呈现出典型的X 型负泊松比变形特性，角度梯度蜂窝结构则呈现出U型变形特性，其吸能及比吸能高于其他蜂窝结构，其中角度正梯度蜂窝结构的第一碰撞力峰值较低。

2）内厚度梯度型蜂窝结构呈现出逐行压溃的I型变形模式，蜂窝结构整体未呈现出双向收缩的负泊松比特性，且内厚度对碰撞力影响较大。

3）高度梯度蜂窝结构与均匀蜂窝结构仅变形模式存在差异，结构更快达到密实极限，吸能效果及碰撞力基本无差异。