高频信号注入法的无传感器运行比较研究

李艺仁，简炜，彭国生，张金亮，陈宇峰，黄新成

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰442002）

在交流传动系统中，为了实现高精度、高动态性能的速度和位置控制，采用磁场定向矢量控制或直接转矩控制［1-2］，一般通过光电编码器、旋转变压器及霍尔传感器等机械传感器来实现转子位置和速度的测量。机械传感器的安装、电缆连接、故障等问题会降低系统的可靠性和稳定性，在电机转速较高的场所中会额外增加电机控制系统的整体尺寸及制作成本，这些因素限制了机械传感器的应用范围。因此学者们逐渐提出无传感器控制技术方案，其主要思想是将电机绕组中有关的电信号提取出来，然后对电信号进行处理，提取出转子位置及速度的相关信息。在这些获取转子位置及速度信息的方法中，多数以检测基波反电动势的方法来实现，但当电机处于低速甚至零速的工况下，基波反电动势很小而难以检测，具有一定的局限性。另外，由于反电动势法主要依赖于基波电压和电流信号来获取转子的位置及速度信息，所以对电机参数非常敏感，鲁棒性较差。为了在永磁同步电机低速及零速的工况下也能准确捕捉到转子的位置和速度信息，一些学者提出了转子凸极追踪法［3-4］。该方法需要持续注入高频激励信号，主要依赖于转子的凸极效应，故对电机参数不敏感，鲁棒性好。

高频信号注入法的主要思想是在电机中注入幅值和频率固定的高频信号，这些信号既可以是电流信号，也可以是电压信号；当这些信号经过电机三相绕组后，会产生对应的高频信号，而这些高频信号中携带与转子位置和速度相关的信息，可用特定的方式将其抽取出来。从注入高频电信号的种类进行划分，大体上可分为旋转高频电压注入法和脉振高频电压注入法，前者要求永磁同步电机交、直轴电感差值较大，即电机具有较大的凸极率；而后者由于高频电压的注入方式不同，会产生“饱和凸级效应”现象［4］，因此可应用于插入式、内置式甚至是隐极的表贴式永磁同步电机中，对永磁同步电机的类型无限制要求。很多专家学者都对2 种高频信号注入法进行了深入的理论研究，却很少直接将它们联系起来进行技术对比，分析其优缺点及各自适用的领域和场合。文中对旋转高频电压信号注入法以及脉振高频电压注入法的工作原理进行详细介绍，通过搭建仿真模型来对比分析2种高频信号注入法的运行情况，并客观评价其优劣。

1 旋转高频电压信号注入法

1.1 工作原理

一般电机的基波频率选择范围为50～60 Hz，而注入的高频信号频率选择范围为0.5～2 kHz，超过电机基波频率的10 倍，因此可将传统的永磁同步电机模型简化为简易RL模型来进行分析。高频时电阻相对于电抗来说小很多，所以忽略不计；此时高频激励下三相永磁同步电机的电压方程为

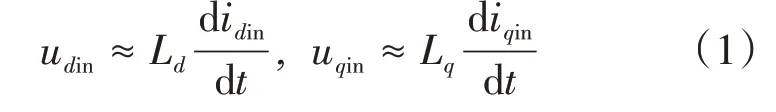
式中：udin、uqin和idin、iqin分别为旋转坐标系d-q 轴的高频电压和高频电流分量；Ld和Lq为定子d 轴和q轴电感。假定注入高频电压信号的频率为ωin，幅值为Vin，则高频电压信号的表达式为

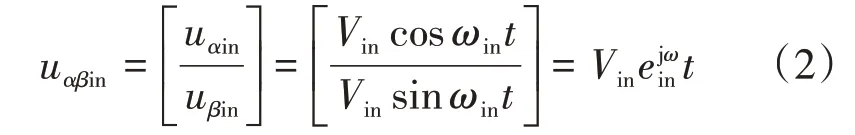
式中：uαin、uβin为静止坐标系α - β 下的高频电压分量。将式（1）变换到同步旋转坐标系下，即

将（3）式变换到静止坐标系中的表达式为

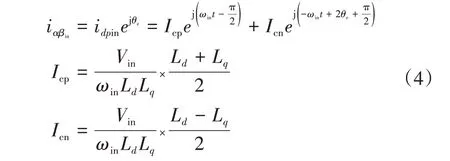
式中：θe为转子实际位置；Icp为正相序高频电流的最大值，而Icn为负相序高频电流分量的最大值。

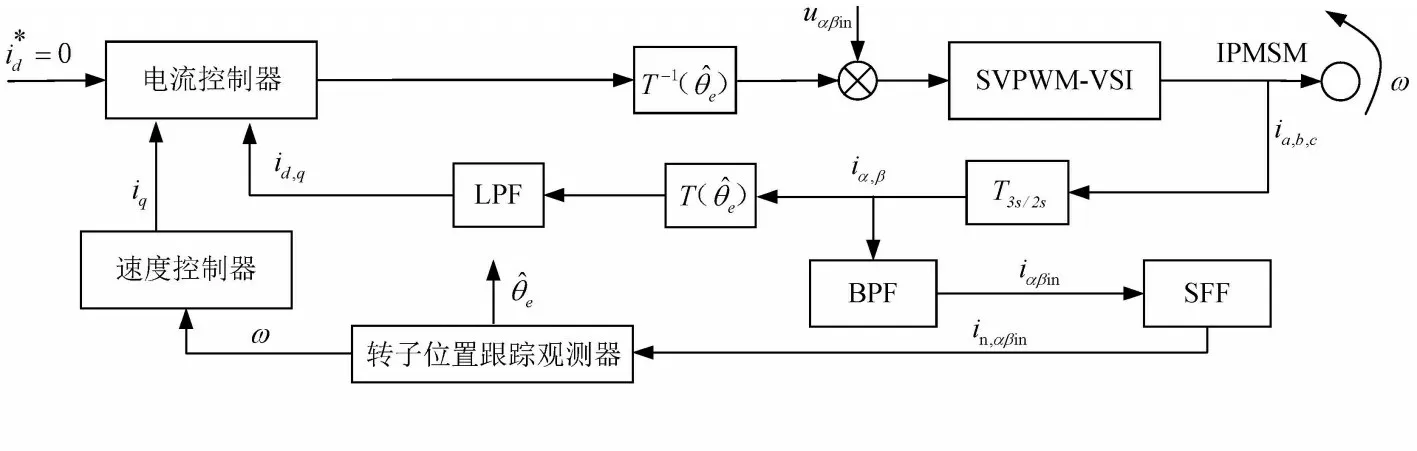
图1 旋转高频电压信号注入法系统原理图

为了准确获取负相序高频电流信号中包含的转子位置、速度信息，必须尽可能地将基波电流、SVPWM 载波频率电流以及正相序高频电流分量滤除，以免对负相序高频信号的检测与提取过程造成较大干扰。由于注入高频电流信号频率约为基波电流信号频率的10倍，而SVPWM载波频率又远高于高频电流信号的频率，因此可通过BPF设置合适的高低通带边缘频率来滤除基波电流和SVP⁃WM 载波频率电流。高频电流信号中的正负相序分量旋转方向相反，考虑用同步轴系高通滤波器将正相序高频电流分量滤除。其思想是通过坐标变换把高频电流矢量变换到与注入高频电压矢量同步旋转的参考坐标系中［5］，将正相序高频电流矢量变为直流，然后通过一般的高通滤波器将其滤除。LPF 的作用是在闭环控制中将混杂在基波电流中的高频电流信号滤除，保证电流闭环不受影响。由于系统中使用了较多数量的滤波器，使得在滤波前后负相序电流分量产生一定的相位滞后，导致转子位置估计值最终滞后于实际转子位置一定的角度，故在系统实现方面需加入对应的角度补偿，其值视电机实际转速的大小而定。

1.2 位置跟踪观测器的设计

对式（4）进行分析可看出：高频电流信号包含正负序2种分量，负相序电流分量包含转子位置信息，且正负相序电流分量旋转方向相反；所以需要设计转子位置追踪观测器来提取转子位置信息并对其进行检测。滤除基波电流和SVPWM 载波频率电流后，式（4）中只剩下提取出来的负相序高频电流信号，该信号中包含了转子的位置和速度信息，用来进行凸极追踪；其矢量信号表达式为

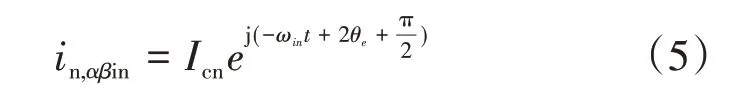
为了得到位置跟踪器所需的位置信息，采用外差法解调空间凸极调制的负相序分量，通过欧拉公式将式（5）写成复数形式，则有

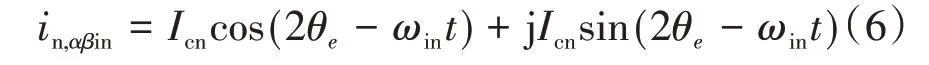
采用外差法的方式是将式（6）中的前后两项分别乘以sin(2- ωint)和jcos(2- ωint)，从而得到转子凸极跟踪表达式为

根据极限思想，当转子位置误差接近0 时式（7）可近似线性化；调节误差信号使之趋近于0，则估计转子位置和实际转子位置θe的差值也趋近于0，此时估计转子位置无限接近于实际转子位置θe的值，再对进行微分，得到估计转子角速度。文中位置跟踪观测器由外差法、PID 调节器、电机机械系统数学模型组成，结构框图见图2。

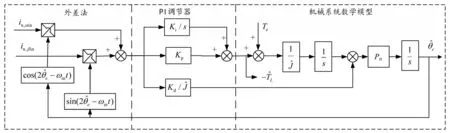
图2 旋转高频电压信号注入法位置观测器

2 脉振高频电压信号注入法

2.1 工作原理

从注入高频信号的方式和位置来看，脉振高频电压信号注入法不需要在坐标系中注入2 个高频信号，而是在估计同步旋转坐标系d-q 中的d 轴上注入1 个幅值和频率固定的高频正弦电压信号。在静止坐标系中，这个信号是脉振的电压信号［6］。

在估计同步旋转坐标系d-q中，系统注入高频电压信号的方程为

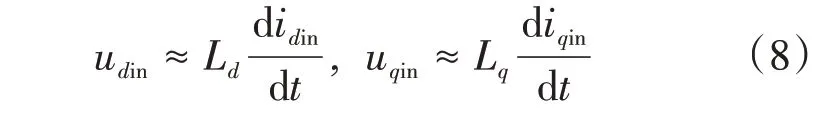
在坐标系d-q中电机交直轴的定子电感为

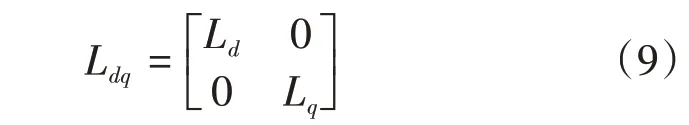
在两相静止坐标系α - β 中，式（9）中的定子电感表达式可写为

注入脉振高频电压信号的表达式为

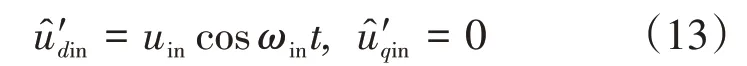
式中：uin和ωin分别为高频电压信号的幅值和频率，将式（13）代入式（12）进行化简可得：

图3 脉振高频电压信号注入法原理图

统结构更加简单，采用的滤波器个数更少［7］，且由于整个矢量控制系统构成了转子位置角的闭环控制，因此转子位置的估算值与实际值得差异很小，不需要进行额外的转子位置角度补偿。

2.2 位置跟踪观测器的设计

由于正弦函数在1个周期内满足条件：

当转子位置估算误差足够小趋近为0时，误差信号的表达式可简化为

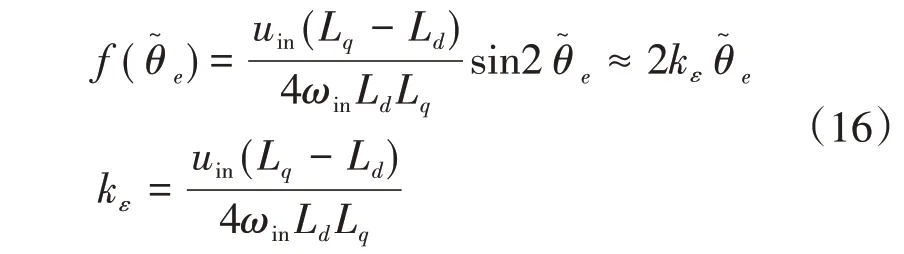
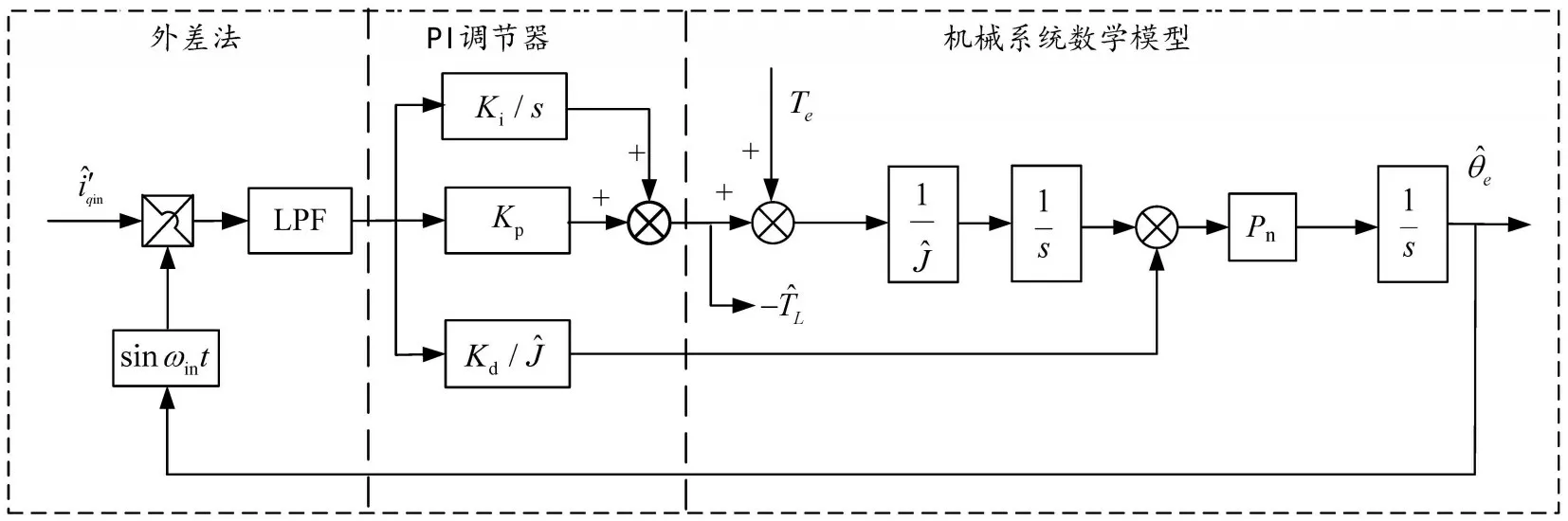
图4 脉振高频电压信号注入法位置观测器

为了更好地与旋转高频电压信号注入法进行比较，利用脉振高频电压信号注入法搭建了转子位置跟踪观测器，实现框图如图4 所示，转子位置误差信号经过转子位置跟踪观测器后就可以得到转子的位置信号。

3 仿真验证对比及分析

在Matlab 2019a 中分别用旋转高频电压信号注入法和脉振高频电压信号注入法搭建仿真模型，在转速估计、转子位置估计等方面对2种仿真模型的结果进行对比和验证，仿真系统基于传统id= 0的控制方式，电机极对数为2；定子电感Ld为5.2 mH，Lq为17.4mH；定子电阻为0.33Ω；磁链为0.646 Wb；转子转动惯量为0.008 kg·m2；阻尼系数为0.008 N·m·s，母线电压设定为311V；载波频率为5 kHz。对于高频载波信号的选择，如果高频信号频率太高，则会使系统产生混杂信号，故一般为0.5～2 kHz；另外高频载波信号的幅值上限由其需要的电能和产生的噪声等因素决定，故一般设定为额定电压的0.05～0.1 倍。最终确定2 种仿真模型中Vin为20 V，高频电压信号频率为1000 Hz，LPF通带边缘频率设置为987 Hz，BPF 低、高通带边缘频率分别设置为987 Hz和1018 Hz。

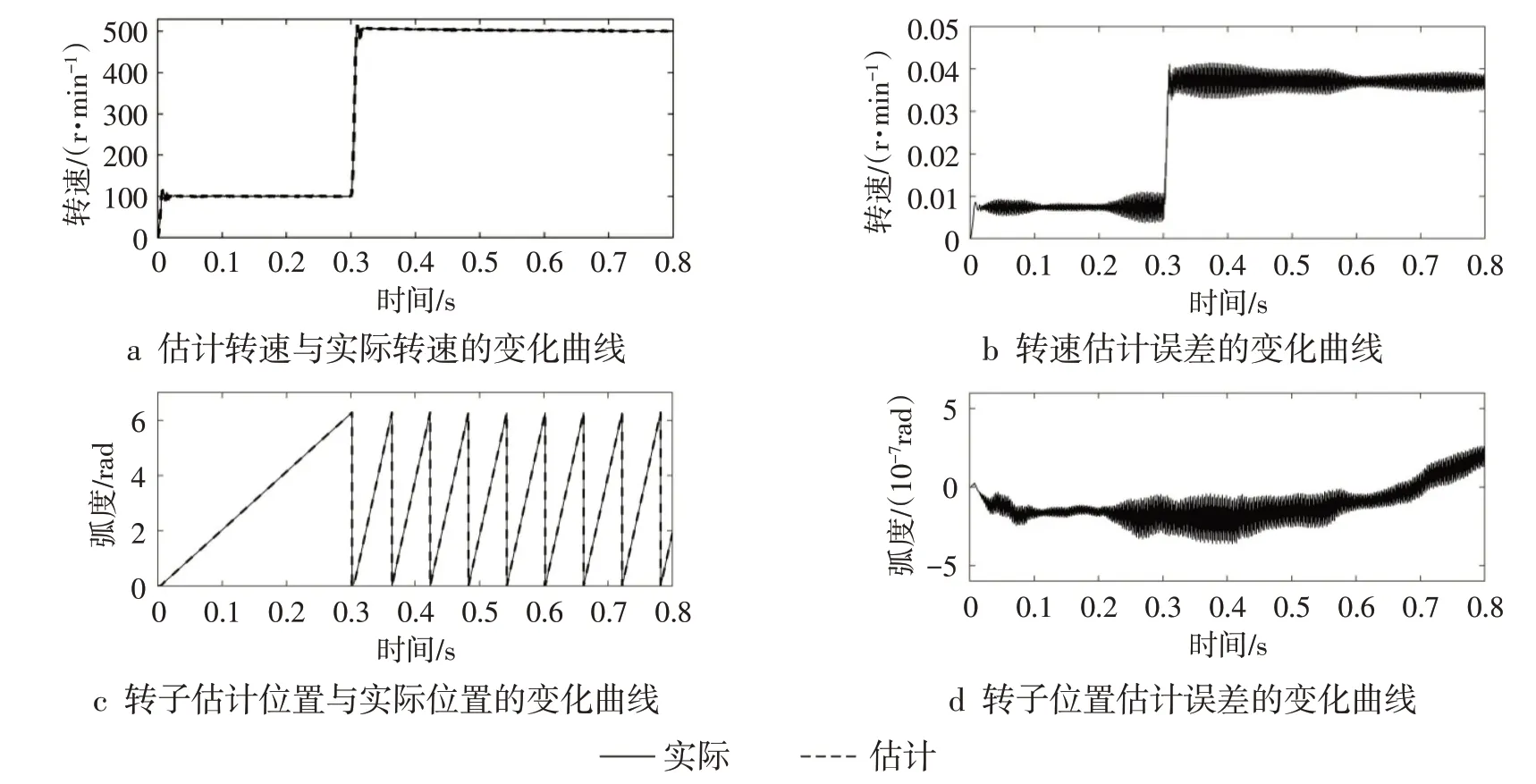
图5 旋转高频电压信号注入法仿真结果

为比较2 种高频信号注入法在低速下的作用效果，设定电机初始转速为100 r·min-1，在0.3 s 时刻升至500 r·min-1，仿真结果如图5～6 所示：当转速为100 r·min-1时，2 种高频信号注入法都有不错的效果，转速误差与位置误差十分小，可以忽略不计；设定转速升至500 r·min-1时，在0.7 s 时2 种方法的转速波形都趋近于稳定，转速误差虽略有增加，但依然控制在±0.05 r·min-1。采用脉振高频电压信号注入法的电机矢量控制系统中，由于整个矢量控制系统构成了转子位置角的闭环控制，系统比较依赖于PID调节器中的参数，但系统调速过程中PID调节器的参数难以及时调整，因此仿真结果中脉振高频电压信号注入法对转速突变时的转子位置误差更大一些；而在调试过程中也发现：由于高频电压信号注入法采用了更多种类和数量的滤波器，造成了估计转子位置角的滞后现象，需要经过精准计算后根据不同转速给估计转子位置角添加对应的角度，这也使系统在结构上变得更加复杂。将2 种方法的最大转子位置误差由弧度单位转化为角度单位后，最大转子位置误差均在0.1°以内，表明2 种方法均能在电机调速系统中精准地测出转子位置及转速，且系统的动静态性能良好。

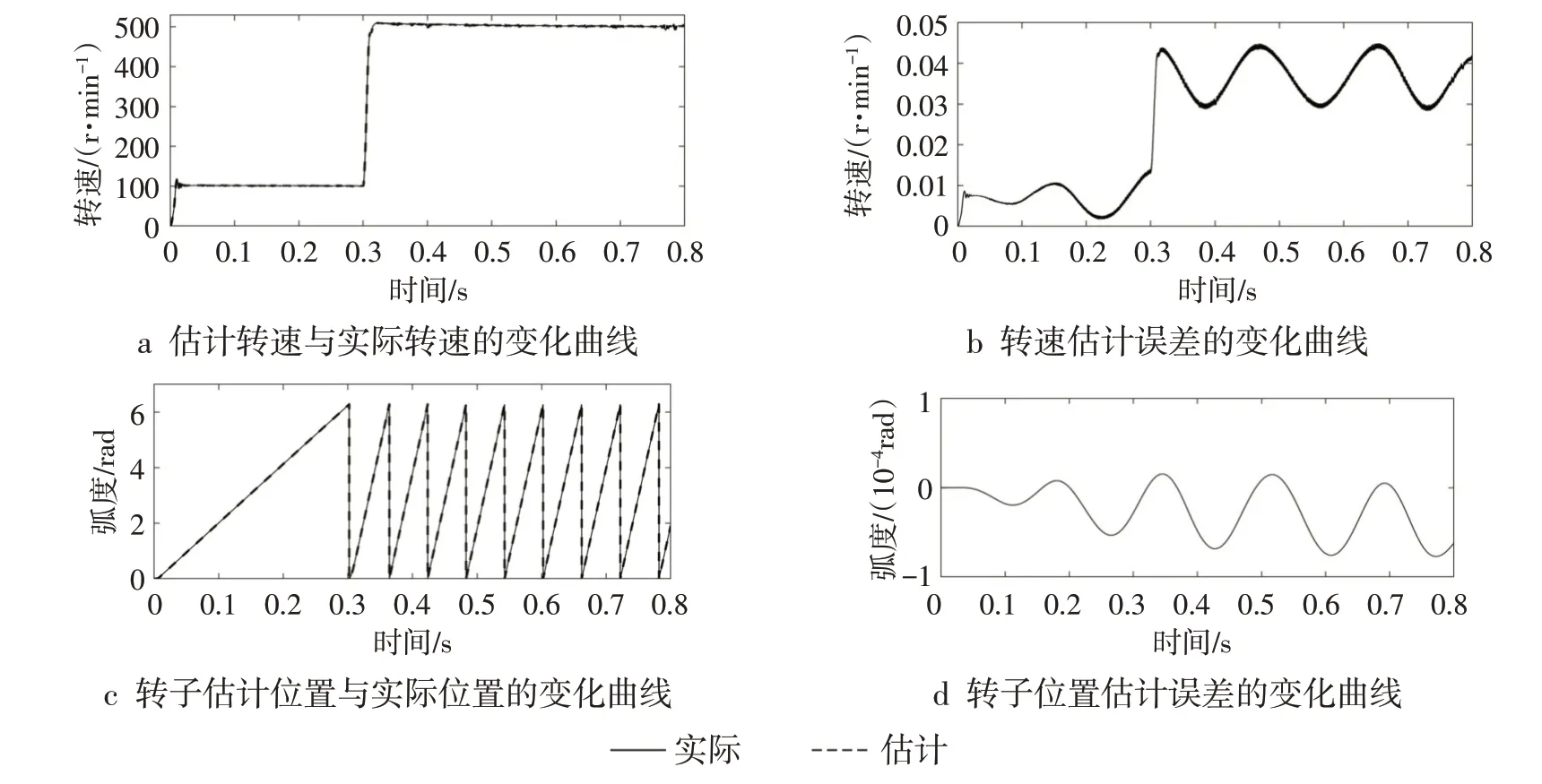
图6 脉振高频电压信号注入法仿真结果

4 结论

通过搭建仿真模型对采用旋转、脉振高频电压信号注入法的无传感电机矢量控制系统进行比较。对仿真结果进行分析可得：2种方法均能在低速下精准地估算出转子速度及位置，具有较强的鲁棒性。旋转高频电压信号注入法构成的系统结构相对复杂，使用了较多种类和数量的滤波器，从而使得转子位置估计角度存在一定的滞后，需要在不同转速情况下补偿相应的转子位置估计角度；其注入方式是在静止坐标系中注入高频正弦电压信号，不受控制策略的影响，在实际系统中更加容易调试和实现。脉振高频电压信号注入法的系统结构相对简单，不用对转子位置估算角进行额外补偿，但对PID调节器的参数较为敏感，且需要在注入高频电压信号时准确确定估计转子同步轴旋转坐标系的位置，故在实现方面相对困难一些。总体来说，2种高频信号注入法都能在中低速条件下有效检测出转子的位置及转速，且都不依赖于电机自身的参数，静动态调速性能较好。