加权有向图社区发现的子系统划分

杨晓峰,谢 巍,张浪文†

(1.华南理工大学自动化科学与工程学院,广东广州 510640;2.广州市标准化研究院,广东广州 510110)

1 引言

现代化学过程通常由相互连接的操作单元组成,它们通过能量和信息流紧密地集成在一起.先进控制算法在应用于这些过程时应满足预定的目标,达到预期的安全,可持续性和经济性水平[1].然而,传统的集中或分散控制架构难以适用于复杂过程系统[2].

近十年来,为提高计算效率,维护灵活性和容错性,分布式控制架构得到快速发展[3].分布式控制系统设计包括两个关键步骤[4]:1)合理地将整个系统划分成较小的子系统,需要保证子系统的能控性、能观性和灵活性等;2)针对每个子系统设计局部控制器及其协调算法.在过去的十年里,分布式控制算法(尤其是分布式模型预测控制)吸引了非常广泛的研究关注[5].然而,与其同等重要的子系统划分问题受到的关注相对较少[6].

近几年来,子系统划分方法取得了一些成果[7–9].文献[7]提出了一种基于层次聚类的分散控制系统分解方法.文献[8]提出了一种既考虑耦合强度又考虑结构紧密性的输入–输出配对方法.另外,文献[9]研究了基于无权重有向图的社区发现子系统划分算法.在社区发现算法中,将一个大规模系统看作一个网络,通过将网络分解为较小的子网络,建立面向分布式控制或估计的子系统模型.

考虑到不同状态和输出变量之间的结构紧密性,已有研究尝试将非线性系统分解为较小的单元,然后设计分布式状态估计[10–11].文献[10]提出了一种面向分布式状态估计的过程网络子系统划分方法.在文献[11],分布式状态估计和控制在一个架构内被共同考虑.上述面向分布式状态估计的子系统划分方法均只考虑过程系统的物理拓扑,而未考虑不同变量之间的连接强度.研究发现,如果不考虑变量间连通性的强弱,可能导致子系统划分的次优或不适当,特别是对于连接强度差异较大的系统影响更大[12].

基于上述分析,本文提出一种面向分布式状态估计的子系统划分方法,构建了加权有向图,既考虑结构的紧密性,又考虑系统状态/输出之间的连接强度.基于加权有向图,利用社区发现算法将所有系统变量划分为较小的群组,使得划分得到的子系统内部关联较强,而子系统之间的耦合强度较弱.

2 问题描述

考虑如下复杂非线性系统的子系统划分问题:

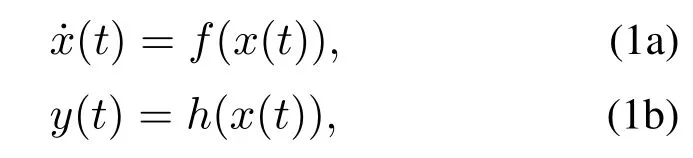
其中:x ∈Rnx表示状态向量,y ∈Rny表示输出向量,f和h分别表示非线性系统状态和输出方程.

本研究的目标是将系统(1)划分成多个子系统,得到第i个子系统的模型,以设计分布式状态估计器

其中:x(i)∈Rnx(i)表示第i个子系统的状态向量,y(i)∈Rny(i)表示第i个子系统的测量输出,X(i)表示所有与子系统i直接关联的子系统状态,i=1,···,p,p是划分得到子系统的个数.在本设计中,假设p是已知的且数量少于测量输出的个数,即pny.

由于本文子系统的划分是面向分布式状态估计设计,对于划分的子系统,需要进行能观性的判断.为了检验非线性系统(1)的能观性,可以判断该系统的能观矩阵是否满秩[13],能观矩阵通过如下方式构建:

其中:Lfh 表示方程h 对方程f 的Lie导数,其定义为表示h对f的r阶Lie导数,定义为如果对于x ∈X,有rank(Q(x))=nx,那么,系统(1)在范围X内是局部可观的[13],否则系统(1)是不可观的.

社区发现算法是一种将大规模复杂网络划分成多个子网络的有效工具[14],通过由文献[15]定义的模块度来评价一个网络划分的好坏.考虑一个带有N个节点的网络,其不加权的邻接矩阵A是一个N ×N矩阵,定义元素Aij为

通常,不考虑节点自身的回路,也就是说邻接矩阵的主对角线上的元素为0.用模块度来评价划分好坏,模块度Q的范围为0到1,社区发现算法通过最大化模块度来找到最优群组(子系统)结构,使得划分的子系统内部的连接数最多,而群组之间的连接数最少.一般模块度Q在0.3到0.7之间时被认为是较好的划分方法,否则表示该系统不适合再进行划分.

然而,实际应用的子系统划分中,仅考虑划分得到的子系统内部连接边数最多是不够的,还需要考虑连接边的连接权重.本文将对系统构造带权重的有向图,并利用模块度最大化方法对系统进行划分,以保证各个划分子系统之间的连接权重最小.

3 基于加权有向图的社区发现子系统划分

本节将提出一种系统化的子系统划分方法,考虑将非系统(1)划分成多个子系统,并设计滚动时域估计算法对子系统状态进行分布式状态估计.

本文方法的主要结构如图1所示.首先,将非线性系统(1)用加权有向图进行描述,其中系统状态和测量输出变量看成网络中的节点,这些节点通过加权连接边进行连接,连接边上的权重反映了节点之间的连接强度.然后,基于加权有向图,利用社区发现算法找到最大模块度,将系统划分成多个子系统群组.最后,通过检测划分子系统的能观性,获得子系统划分结果.

3.1 加权连接边的定义

本文将利用加权有向图对系统(1)进行描述,具体来说,将所有的状态和测量输出变量当做有向图的节点,这些节点通过有向边进行连接.令fi表示向量方程f的第i(i=1,···,nx)行,hj表示向量方程h的第j(j=1,···,ny)行,xi表示状态向量x的第i(i=1,···,nx)行,yj(j=1,···,ny)表示输出变量y的第j行.

在已有的无权重有向图中,不同变量(节点)之间的连接强度未被考虑.为获得权重,对非线性系统在工作点xs求一阶偏导得到有向图中连接边的敏感度

图1 本文子系统划分结构Fig.1 Flowchart of the proposed subsystem decomposition

定义如下连接边的权重:

状态变量xi到另一个状态变量xl连接边的权重定义为(l,i=1,···,nx)

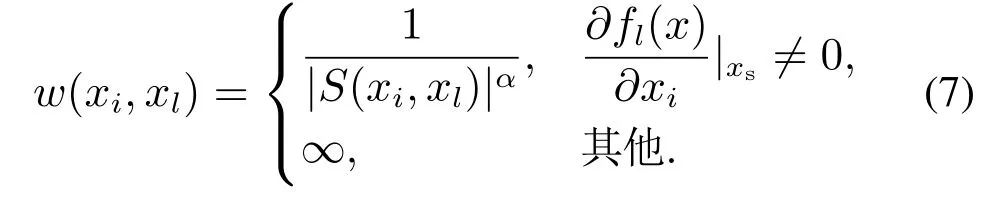
状态变量xl到测量输出变量yj连接边的权重定义为(l=1,···,nx,j=1,···,ny)

其中α是一个介于[0 1]的参数,用于调节连接边的权重在子系统划分过程中的重要性,当α=0时,所有连接边的权重为1,即等效于已有的无权重有向图;当α增加时,连接边的权重将在子系统划分中更多地被考虑.当S(xl,yj)=0或S(xi,xl)=0时,连接边的权重为无穷,即两个节点之间没有直接连接.

由于不同的α值将影响子系统的划分结果,如何选择合适的参数α对子系统划分相当重要.总体而言,当有向图中所有连接边的敏感度差异很小时,在子系统划分时应重点考虑连接边的数量,此时选择较小的α即可.相反,当所有连接边的敏感度差异很大时,应更多地考虑连接边的权重对子系统划分的影响[16].

3.2 最短路径

为实施社区发现算法,需要构造加权邻接矩阵,因此首先应找到有向图中的一个节点到另一个节点的最短路径.令P表示一个状态变量到另一个状态变量或输出变量的路径,在这条路径P中的所有连接边表示为e ∈P.路径L(P)的长度可以计算得到

其中:l=1,···,nx, j=1,···,ny,Plj,Plj表示从状态xl到输出yj所有路径和其中一条路径.本文利用Dijkstra’s算法[17]找到任意两个节点的最短路径,其计算复杂度为O(E log V),其中V 和E分别是节点的数量和连接的边数.

3.3 构建邻接矩阵

本节将构建非线性系统(1)的邻接矩阵.对于系统(1)所形成的有向图,总共有na(其中na=nx+ny)个顶点.令ca为状态和测量输出向量,定义为ca=[x1,···,xnx,y1,···,yny].

那么,所构建的加权邻接矩阵Aw将被用于社区发现算法,以对系统(1)进行划分.上述定义的加权邻接矩阵(15)是无权重邻接矩阵[14]的扩展,其主要区别是:a)加权邻接矩阵考虑了两个节点之间连接的权重,而文献[14]只考虑了两个节点之间的连接度;b)本文方法中,考虑了两个节点之间的最短路径,因此,邻接矩阵中的0元素表征了两个节点之间没有连接.

3.4 寻找最大模块度

模块度Qw既考虑了灵敏度,又考虑了边的数量.子系统划分问题等价于通过寻找最大化的模块化Qw进行社区结构发现.首先,需要进行初步的群组配置,群组结构的初始化基于如下假设:i)每个群组至少有一个测量输出;ii)应将直接影响yi的系统状态分配给属于yi同一个群组.初始化群组结构步骤如下:

步骤1定义关于复杂系统的群组结构sw(0)=[cx1(0) ··· cxnx(0) cy1(0) ··· cyny(0)],其中cη(0)表示每个节点xi(i=1,···,nx)或yj(j=1,···,ny)的群体标签.应用快速二分法(如文献[18])寻找最大模块度Qw时,在sw中的第i个变量被分配到第i个群体,i=1,···,na,即(0)=[1 ··· na].

步骤2对于每个状态变量xi,i=1,···,nx,找到所有和状态变量xi关联的测量输出,在¯sw(0)中将相应的元素标为相同编号.

步骤3对于每个测量输出yj,j=1,···,ny,找到所有和输出方程hj(·)关联的状态变量,并将这些状态标量标为和yj相同的编号.

步骤4所得到的分组(0)即可作为实施社区发现算法的初始群组.

得到的初始群组结构将用于寻找子系统分解中模块度的最大值.在所提出的方法中,子系统(即式(2)中的p)的数量应预先设定.在本文中,快速二分法用于最大化模块度[18],其步骤如下:

步骤1对每个节点i实施如下算法:

步骤1.1对于节点i的每个邻居节点j,通过将节点i从当前群组移动到节点j所在的群组,计算模块度的变化值∆Qw.

步骤1.2找到上一步中最大的∆Qw>0,将顶点i放入到相应的群组中(即将节点i编入最大∆Qw相应的分组),得到新的分组.

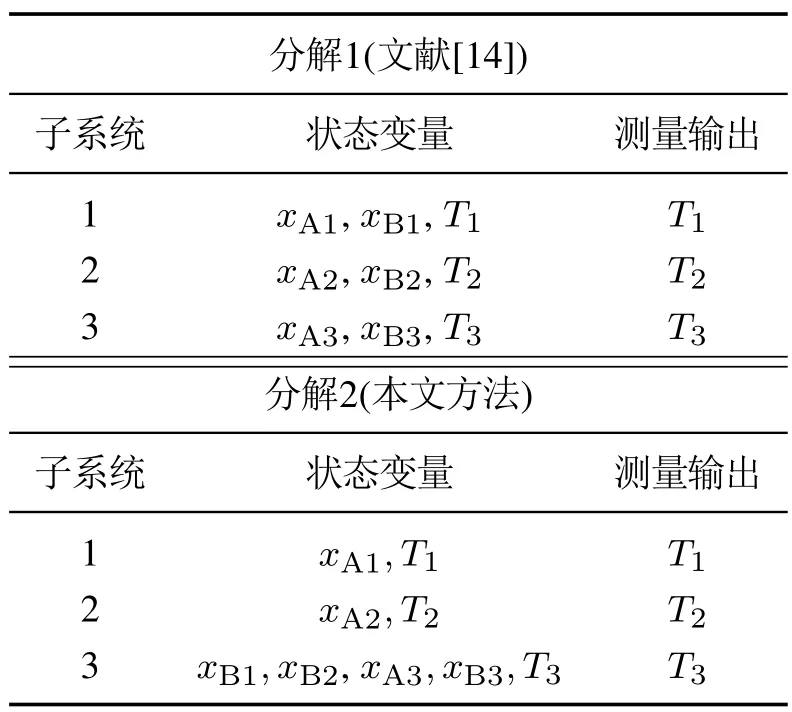
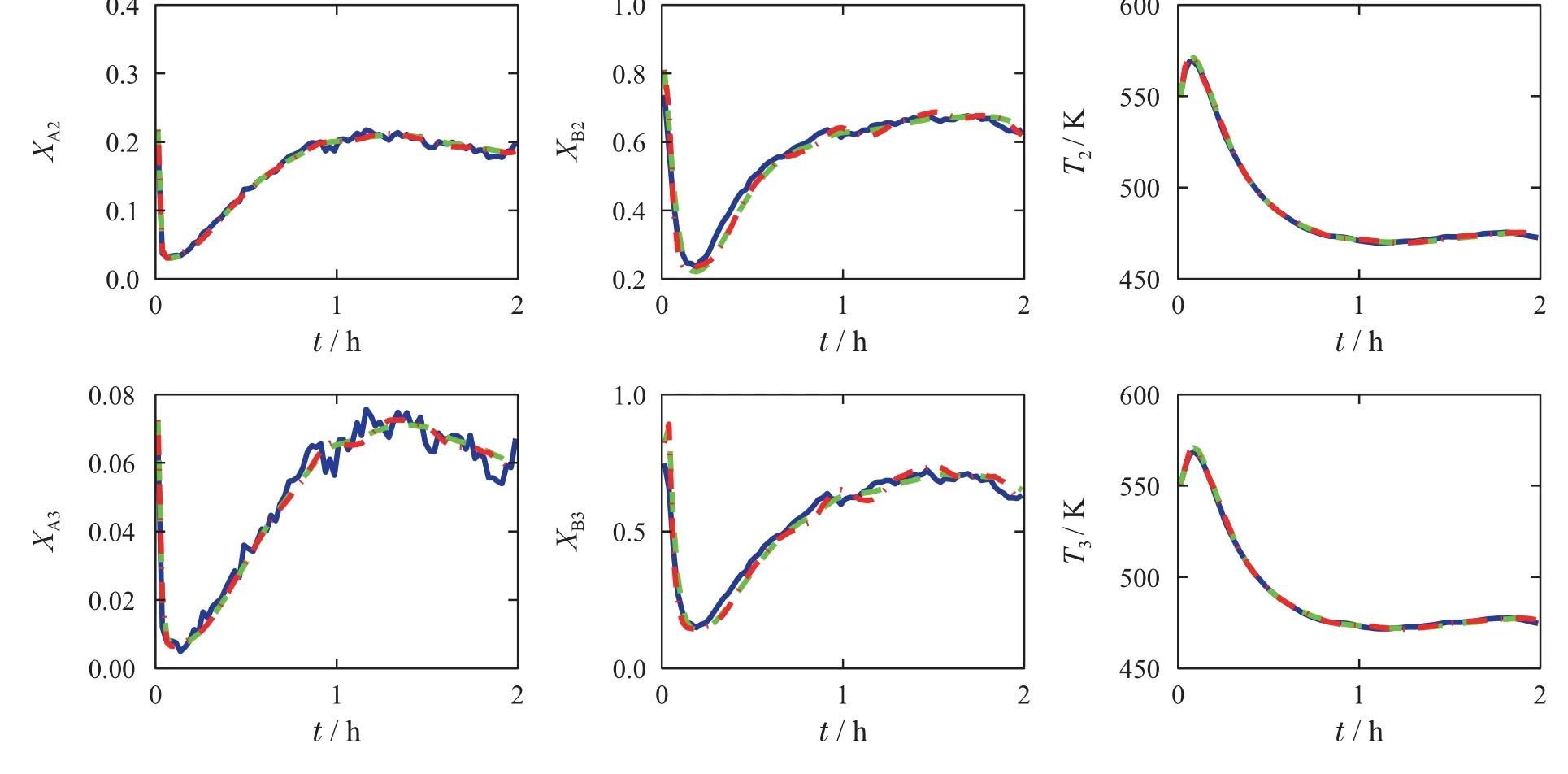
步骤2令nc(k+1)作为节点集结后的群组数量,如果nc(k+1)

3.5 分布式滚动时域估计设计

为对子系统的划分结果进行分析,本文将对所得到的子系统应用于分布式滚动时域估计算法,并说明考虑加权有向图的必要性.本文提出分布式滚动时域估计算法,局部估计器通过共享的通信网络进行信息交互.子系统i的局部估计器为求解如下优化问题:

4 实例应用

本节考虑将所提出的子系统划分及分布式滚动时域估计算法应用于反应–分离过程系统[19],该过程包括两个连续搅拌反应釜和一个快速分离釜(见图2).第一个连续搅拌反应釜包含反应物J,其给定蒸汽为F10,然后产出产品K.然后,产品K在第2个反应釜中转换成最终产品L.

图2 反应–分离过程系统Fig.2 Reactor-separator process

其中:xAi,xBi表示产品J,K在容器i(i=1,2,3)中的质量分数;xC3表示产品L在反应釜3中的质量分数;Ti容器i(i=1,2,3)中液体的温度;T10,T20表示输入到容器1和2的蒸汽温度;F1,F2表示物料从容器1和2流出的流速;F10,F20表示物料从容器1和2流出的稳态流速;Fr,Fp分别表示产品的循环和废弃流速;Vi表示容器i(i=1,2,3)的体积;E1和E2表示反应过程1和2的催化剂;k1和k2表示反应过程1和2的指前因子值;∆H1和∆H2表示反应过程1和2的热量;αA,αB,αC表示物质J,K,L的相对挥发率;Q1,Q2,Q3分别表示容器i(i=1,2,3)的热量输入;Cp热容量;R表示气体常数;ρ表示溶液浓度.

相关模型参数参见表1.

表1 模型参数Table 1 Model parameters

该反应–分离过程的其中一个稳定工作点为

为实现利用测量输出Ti(i=1,2,3)对系统状态xAi,xBi,Ti(i=1,2,3)的估计,首先对子系统进行划分,并和已有的子系统划分方法(文献[14])进行比较,得到如表2所示的划分结果.

表2 子系统划分结果Table 2 Decompositions for the CSTR process

在应用分布式估计算法时,如果进行实时信息交互,分布式估计器的通信成本较高,因此希望子估计器之间可以在较少通信交互的同时获得较好的估计效果.如图3所示,应用分布式滚动时域估计算法时(通讯间隔n=1),基于子系统划分2的估计效果比基于子系统划分1获得了更好的效果,本文提出的基于加权有向图的子系统划分方法比未考虑连接权重的分解算法具有更小的估计误差.

图3 当n=1时,实际状态轨迹(蓝色实线)、基于分解1的状态估计(绿色虚线)和基于分解2的状态估计(红色点划线)Fig.3 The trajectories for n=1 of the actual states(blue solid lines),estimated states based on Decomposition 1(green dashed-dot lines)and Decomposition 2(red dashed lines)

图4 当n=3时,实际状态轨迹(蓝色实线)、基于分解1的状态估计(绿色虚线)和基于分解2的状态估计(红色点划线)Fig.4 The trajectories for n=3 of the actual states(blue solid lines),estimated states based on Decomposition 1(green dashed-dot lines)and Decomposition 2(red dashed lines).

考虑不同的通信间隔n=1,2,3,对分布式滚动时域估计算法进行测试.如表3和图4(通信间隔n=3)所示,随着通信间隔的增加,基于分解1的状态估计效果受到较大的影响.而对于基于本文方法的分解2,由于子系统之间的关联较弱,因此较大的通信间隔对估计性能的影响并不大.其现实意义是在保证估计效果的同时,可以减轻分布式状态估计设计过程中子系统通信的次数,降低通信成本.

表3 不同通信间隔对估计性能的影响Table 3 Summary of the estimation performance

5 总结

本文提出一种基于加权有向图的社区发现子系统划分方法,并应用于分布式状态估计设计中.基于耦合关联的强度研究了一种系统化的复杂大系统分解方法,根据系统的动态模型自动构建系统的加权有向图,进而获得系统的划分,得到的子系统内部的关联远强于子系统之间的关联.这类分解方能够为在复杂系统的分布式状态估计和控制奠定基础,同时也对研究复杂网络的特性具有重要作用.未来可扩展到带系统输入的复杂系统划分方法,及其对分布式控制策略下的性能提升研究,通过分布式状态估计和控制,对该子系统划分方法进行系统的评估.