基于复合抗扰的溶解氧浓度控制

魏 伟,陈 楠,左 敏,刘载文

(北京工商大学计算机与信息工程学院,北京 100048;北京工商大学农产品质量安全追溯技术及应用国家工程实验室,北京 100048;食品安全大数据技术北京市重点实验室,北京 100048)

1 引言

近年来,随着工业化和城镇化的高速发展,人们对淡水资源的需求逐年增加,工业废水与生活污水排放量剧增,严重超过生态系统的承载能力[1];污水处理率不高、处理效果不达标,造成水资源匮乏严重[2],缺水已成全球的共性问题.为解决缺水问题,实现生态环境的可持续发展,污水处理已成人们关注的焦点.

活性污泥法是一种基于生化反应的污水处理方法,该方法处理污水的效果好、效率高,已广泛应用.活性污泥法利用好氧微生物处理污水,溶解氧浓度直接影响水处理效果.提高水处理效果和效率,溶解氧浓度的自动控制非常关键,各种方法相继应用,如:PID控制、基于模糊神经网络的控制、滑模控制等[3–5].然而,污水处理是一个动态过程,其非线性、时变性、耦合性强;同时,出水水质受进水流量、组分、浓度等诸多变化因素[6]的影响.因此,被动接受偏差而产生控制作用的PID控制无法获得满意的控制效果[4].基于模糊神经网络的溶解氧浓度控制具有一定的自学习和逼近能力,但结构固定的神经网络无法很好地处理诸多不确定因素,适应复杂工况[7].滑模控制虽具有较好的鲁棒性,但其最大不足在于控制量的抖振[8].

实际上,若将非线性、时变、耦合因素,以及波动的进水流量、水温、组分、浓度等因素均视为影响出水水质的扰动,从主动抗扰的角度,研究污水处理的抗扰调控,可望获得期望的调控效果.滑模控制具有较强的抑制扰动的能力,扩张状态观测器(extended state observer,ESO)能够实时估计总扰动并通过控制律补偿扰动[9].本文结合滑模控制与扩张状态观测器的优势,针对污水处理过程受多源干扰影响的特点,提出污水处理过程溶解氧浓度控制的复合抗扰控制策略.利用ESO 估计总扰动并通过控制律予以补偿,设计滑模控制抑制未被完全补偿的扰动,既发挥了滑模控制鲁棒性强、设计简单的优势,又在一定程度上解决了滑模控制的抖振问题,提高了污水处理效果,降低了能耗.

2 BSM1结构

污水处理过程1号基准模型(benchmark simulation model No.1,BSM1)模拟了污水处理的布局、进水负荷及生化处理过程,提供了污水处理过程控制公认的评价标准.BSM1中包含晴天、雨天和暴雨天3种天气情况下14天的污水流量及13种组分的变化[10].BSM1模型由生化反应池和二次沉淀池组成(如图1所示)[11].其中:Qi表示相应位置的水流量,Zi表示相应水流中各组分浓度.

图1 BSM1结构Fig.1 Structure of the BSM1

生化反应池为活性污泥1号模型(activated sludge model No.1,ASM1)[12].其中:前2个反应池为缺氧池(V1=V2=1000 m3),发生反硝化反应;后3个反应池为好氧池(V3=V4=V5=1333 m3),发生硝化反应.二沉池(V=6000 m3,底面积A=1500 m2,每层高zj=0.4 m, j=1 ∼10)分为10 层,采用双指数沉降速度模型[13].最上层输出即为达到排放标准的水,最底层为排出的废弃物.

好氧池的溶解氧浓度直接影响氮的去除,进而影响污水处理效果.因此,需控制第5个反应池的溶解氧浓度.第5个反应池的溶解氧变化为[4]

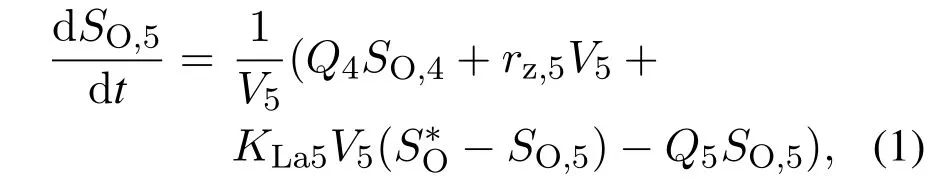
其中:V5为第5个反应池的体积(1333 m3),Q4为第4个反应池的出水流量,SO,4为第4个反应池的溶解氧浓度,KLa5为第5个反应池的氧转移系数,为溶解氧的饱和浓度(8 g/m3),Q5为第5个反应池的出水流量,SO,5为第5个反应池的溶解氧浓度,rz,5表示反应速率.

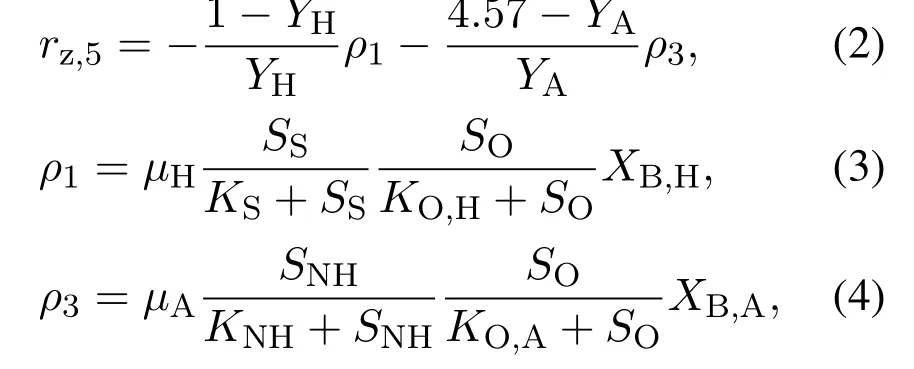
其中:XB,A,XB,H分别为第5个反应池的自养菌和异养菌,SS为第5个反应池的快速可生物降解有机碳,SO为第5个反应池的溶解氧浓度,SNH为第5个反应池中和NH3浓度,式(2)–(4)中其余参数值见表1–2.

表1 化学计量参数Table 1 Stoichiometric parameters

表2 动力学参数Table 2 Kinetic parameters

通常,误差绝对值积分(integral of absolute error,IAE)、误差平方积分(integral of squared error,ISE)及总成本指数(overall cost index,OCI)用于评价不同控制策略的调控效果[6,14].

3 复合抗扰控制设计

由式(1)知,第5个反应池的溶解氧浓度SO,5受前几个反应池的溶解氧浓度、水流量以及第5个反应池溶解氧转化速率rz,5等因素的影响.同时,由式(2)–(4)可知,rz,5中包含可生物降解有机碳SS、异样菌XB,H、氨氮SNH、自养菌XB,A等组分.在实际处理过程中,这些组分浓度随时间变化大、各组分之间相互耦合,微生物种群的生化反应规律尚无法完全辨识,组分测量成本较高或难以实时测量.因此,污水处理过程的溶解氧浓度受到强烈的非线性、耦合以及不确定性的影响,要保证溶解氧浓度控制效果、提高出水水质,对溶解氧浓度控制带来了极大的挑战.此外,受季节、天气、进水流量、组分、浓度等诸多因素的影响,无法建立污水处理过程的精确模型.因此,对模型信息依赖小的控制方法,可获得期望的污水处理过程控制效果.

溶解氧浓度动态特性(1)可改写为

由上述分析,Q4,Q5(第4,5反应池的出水流量),SO,4(第4个反应池的溶解氧浓度),以及f均处于动态变化之中.因此,式(5)仅从形式上反映第5个反应池的溶解氧浓度变化,其精确动态无法获得.

基于污水处理的特点及溶解氧浓度的控制要求,设计图2所示复合抗扰控制.扩张状态观测器估计扰动,滑模控制抑制未被完全补偿的扰动.

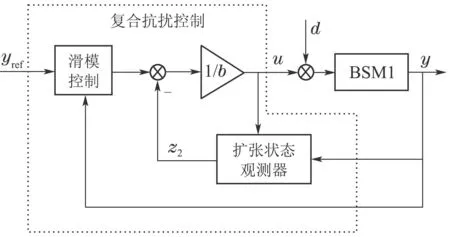
图2 溶解氧浓度的复合抗扰控制结构Fig.2 Compound disturbance rejection control of the dissolved oxygen

3.1 扩张状态观测器设计

根据溶解氧浓度方程(5),充分利用可获取的信息,可设计扩张状态观测器为[15]

其中:z1为y的估计值,y为第5个反应池中的溶解氧浓度SO,5.考虑到Q4,Q5,SO,4,SO,5可由流量计及溶解氧分析仪测得,V5为已知的设计参数,在ESO的设计中,引入.式(5)中的f由z2估计,β1,β2为ESO的增益,为观测器带宽.

3.2 控制器设计

对于第5个反应池的溶解氧浓度,设计滑模面

其中r为溶解氧设定值.

基于扩张状态观测器和滑模控制的复合抗扰控制律为

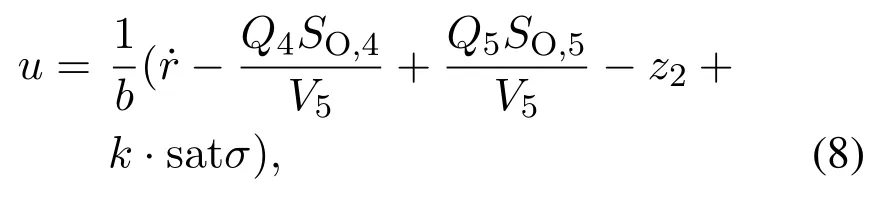
其中k为切换增益且k >0.

3.3 稳定性分析

对式(7)定义的滑模面求导,有

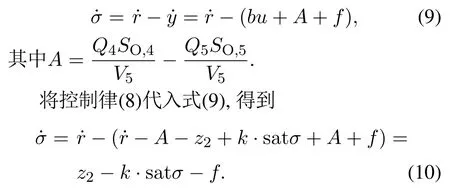
复合抗扰控制律(8)作用下的污水处理溶解氧浓度控制有如下定理.

定理1污水处理溶解氧浓度控制的复合抗扰控制律(8)的切换增益k >k∗时,在扩张状态观测器(6)和控制律(8)的作用下,闭环系统的输出能够沿着滑模面在有限时间内跟随设定值.

证令总扰动估计误差ed=f −z2.由文献[16]知,选择合适的观测器增益,可使扰动估计误差ed有界,即,ESO 收敛.此时,若滑模控制稳定,则闭环系统稳定.

因此,取李雅普诺夫函数

时间内到达设定的滑模面σ=0.也就是说,系统输出可在有限时间内跟随设定值. 证毕.

4 数值仿真

本节以BSM1模型模拟3种天气的污水处理过程.在第7天加入正弦扰动时,对比复合抗扰控制(compound disturbance rejection control,CDRC)、自抗扰控制(active disturbance rejection control,ADRC)、滑模控制(sliding mode control,SMC)以及BSM1提供的PI控制调控溶解氧浓度的效果(控制参数见表3).仿真中,溶解氧浓度设定为2 mg/L,仿真时间为14天.

表3 PI,SMC与CDRC参数Table 3 Parameters of PI,SMC and CDRC

采用误差绝对值积分(integral of absolute error,IAE)、误差平方积分(integral of squared error,ISE)及总成本指数(overall cost index,OCI)定量比较不同控制策略的调控效果:

其中:e=r −y,AE为曝气能,PE为泵能,SP为污泥总量,EC为外部碳源消耗,ME为混合能.

其中:CODEC=400000 g COD/m3,T=tf−t0,其余各变量的物理意义及参数取值参照文献[17].

考虑晴天、雨天和暴雨天时溶解氧浓度的调控情况.

①晴天时,3种调控方法的溶解氧浓度控制响应和调控信号如图3所示.

图3 晴天的溶解氧调控效果及调控信号Fig.3 Control variable and the dissolved oxygen concentration in dry weather

可见,晴天时,4种方法均可调控溶解氧浓度.但CDRC控制溶解氧浓度的效果最好,并且CDRC控制信号的波动大小与其他控制方法的控制信号波动类似.表4所列性能指标显示,与PI相比,CDRC的IAE指标提高了54.6%,ISE指标提高了78.9%,OCI指标几乎相同;与SMC相比,IAE指标提高了81.8%,ISE指标提高了95.7%,OCI指标大小相似;与ADRC相比,IAE指标提高了54.4%,ISE指标提高了78.7%,OCI指标相似.

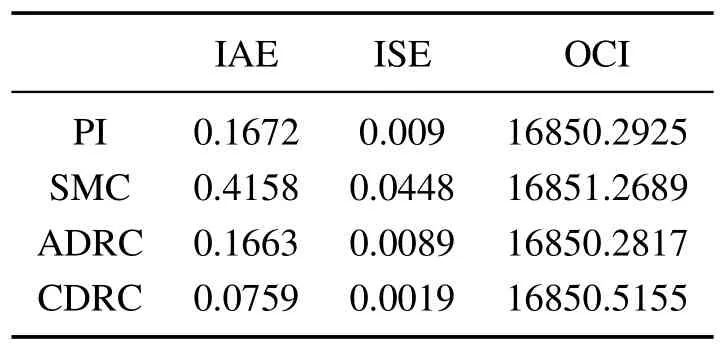
表4 晴天时3种控制的性能指标Table 4 Performance indexes under dry weather

第7天加入幅值为5的正弦信号(5sin(5t))为输入端扰动,溶解氧调控效果及控制量如图4所示.

图4 晴天的溶解氧调控效果及调控信号(存在正弦扰动)Fig.4 Control variable and the dissolved oxygen concentration in dry weather(with sinusoidal disturbance)

图4(a)显示,加入正弦扰动时,CDRC调控的溶解氧浓度与期望值偏差最小、效果最好.图4(b)表明CDRC的控制量波动大小与其他控制方法的相似.同时,表5亦显示,与PI相比,CDRC的IAE提高了54.5%,ISE提高了79.1%,OCI几乎相同;与SMC相比,IAE 提高了81.7%,ISE 提高了95.8%,OCI 指标几乎相同;与ADRC相比,IAE指标提高了54.3%,ISE指标提高了78.9%,OCI指标相似.

表5 晴天时3种控制的性能指标(存在正弦扰动)Table 5 Performance indexes under dry weather(with sinusoidal disturbance)

②雨天时,3种调控方法的溶解氧浓度、调控信号如图5所示.

图5 雨天的溶解氧调控效果及调控信号Fig.5 Control variable and the dissolved oxygen concentration in rain weather

图5(a)显示,雨天时,CDRC控制的溶解氧浓度与期望值偏差仍最小;图5(b)表明4种控制信号的波动亦相似.同时,从表6 可知,与PI 相比,CDRC 的IAE指标提高了55.1%,ISE指标提高了78.9%,OCI指标几乎相同;与SMC相比,IAE指标提高了82.3%,ISE指标提高了96.6%,OCI指标提高了0.03%;与ADRC相比,IAE指标提高了54.4%,ISE指标提高了78.4%,OCI指标大小相似.

表6 雨天时3种控制的性能指标Table 6 Performance indexes under rain weather

第7天加入幅值为5的正弦信号(5sin(5t))为输入端扰动,溶解氧调控效果及控制量如图6所示.

图6 雨天的溶解氧调控效果及调控信号(存在正弦扰动)Fig.6 Control variable and the dissolved oxygen concentration in rain weather(with sinusoidal disturbance)

图6显示CDRC以相似的控制量波动获得最好的溶解氧浓度调控效果.表7同样显示,CDRC比PI的IAE指标提高了55.0%,ISE指标提高了78.9%,OCI指标几乎不变;比SMC 的IAE 指标提高了82.8%,ISE 指标提高了96.7%,OCI 指标提高了0.03%;与ADRC 相比,IAE 指标提高了54.4%,ISE 指标提高了78.8%,OCI指标相似.

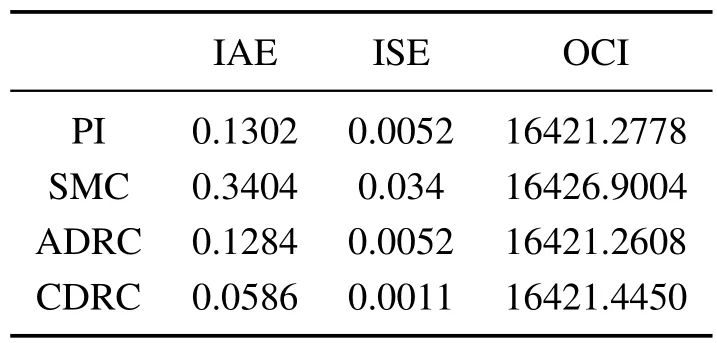
表7 雨天时3种控制的性能指标(存在正弦扰动)Table 7 Performance indexes under rain weather(with sinusoidal disturbance)

③暴雨天时的溶解氧浓度调控效果以及调控信号如图7所示.

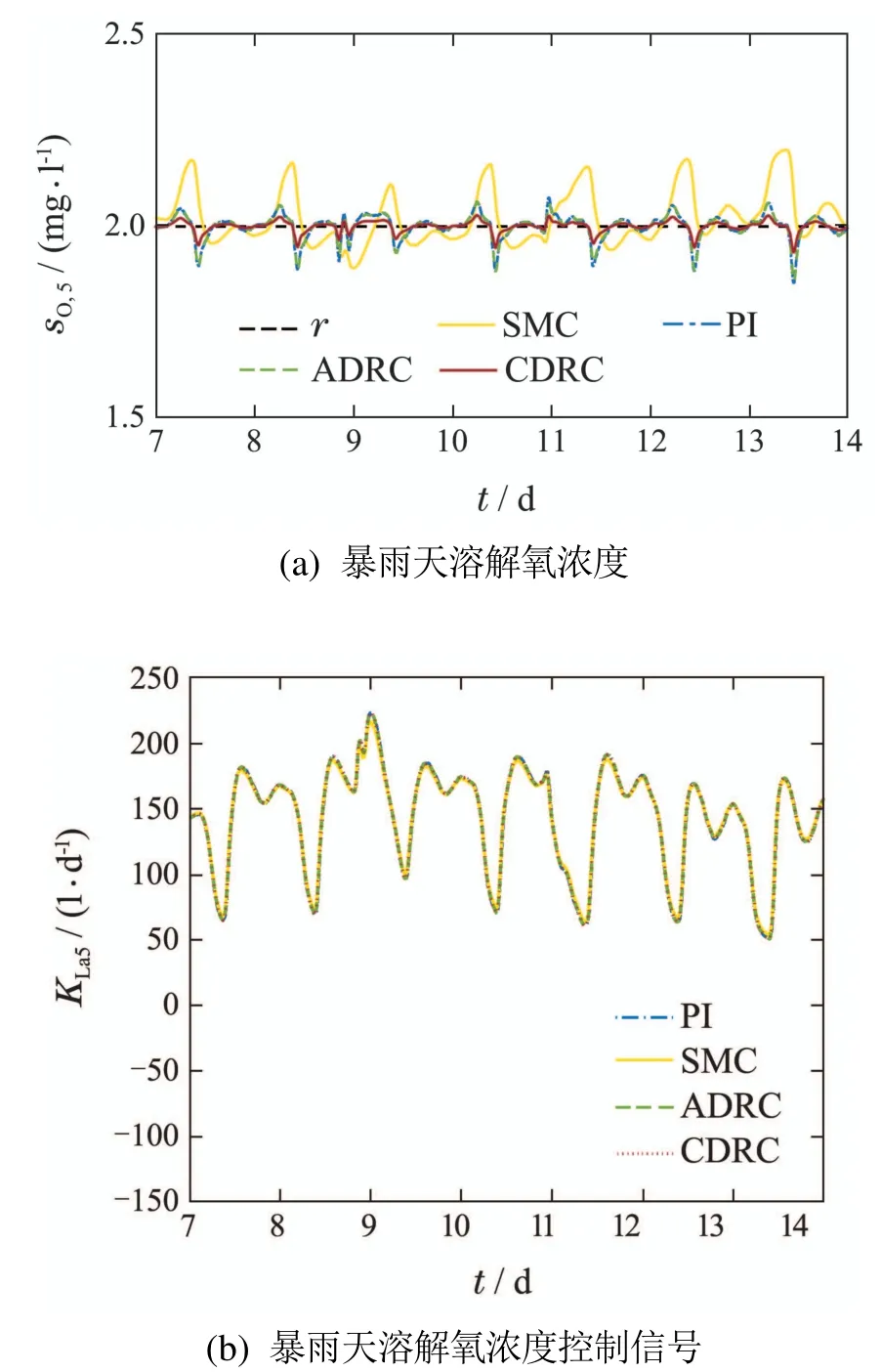
图7 暴雨天的溶解氧调控效果及调控信号Fig.7 Control variable and the dissolved oxygen concentration in storm weather

图7结果依旧表明,CDRC控制溶解氧浓度的效果最好、控制量波动与其他控制方法相似.表8中的数据显示,CDRC比PI的IAE指标提高了55.2%,ISE指标提高了79.7%,OCI指标几乎相同;比SMC的IA E指标提高了81.6%,ISE指标提高了96.0%,OCI指标几乎不变;与ADRC相比,IAE指标提高了54.2%,ISE指标提高了78.8%,OCI指标相似.

表8 暴雨天时3种控制的性能指标Table 8 Performance indexes under storm weather

第7天同样加入幅值为5的正弦扰动(5sin(5t)),溶解氧调控效果及控制量曲线如图8所示.

图8 暴雨天的溶解氧调控效果及调控信号(存在正弦扰动)Fig.8 Control variable and the dissolved oxygen concentration in storm weather(with sinusoidal disturbance)

图8表明CDRC控制的溶解氧浓度效果最好.表9显示,CDRC比PI更优,IAE指标提高了55.2%,ISE指标提高了80%,OCI指标大致相同;与SMC相比,CDRC的IAE指标提高了81.8%,OCI指标几乎相同,ISE指标提高了96.2%;与ADRC 相比,IAE指标提高了54.3%,ISE指标提高了79.2%,OCI指标相似.

表9 暴雨天时3种控制的性能指标(存在正弦扰动)Table 9 Performance indexes under storm weather(with sinusoidal disturbance)

由上述实验结果可知,3种天气情况下,SMC的调控效果不及PI,ADRC和CDRC.这表明,当各种非线性、强耦合及不确定性存在时,要实现期望的控制效果,SMC需要消耗较大的能量.3种天气情况下,CDRC的IAE和ISE指标均最小,这表明CDRC能以较低的能耗获得最佳的调控效果.

此外,由表4–9可知,在有无输入端正弦扰动时,CDRC 的IAE和ISE指标近乎相同.这表明,在ESO及控制律的共同作用下,CDRC能够很好地估计、补偿、抑制扰动,获得期望的控制性能,鲁棒性好.同时,在同样的扰动补偿作用下,CDRC的控制效果皆优于ADRC,这表明CDRC中的滑模控制能够抑制未补偿的扰动,能够进一步提高控制效果.3种天气情况下,输入端加入正弦扰动时,ESO 估计总扰动的效果如图9所示.可见,ESO均能很好地估计总扰动,这是保证调控效果的前提.

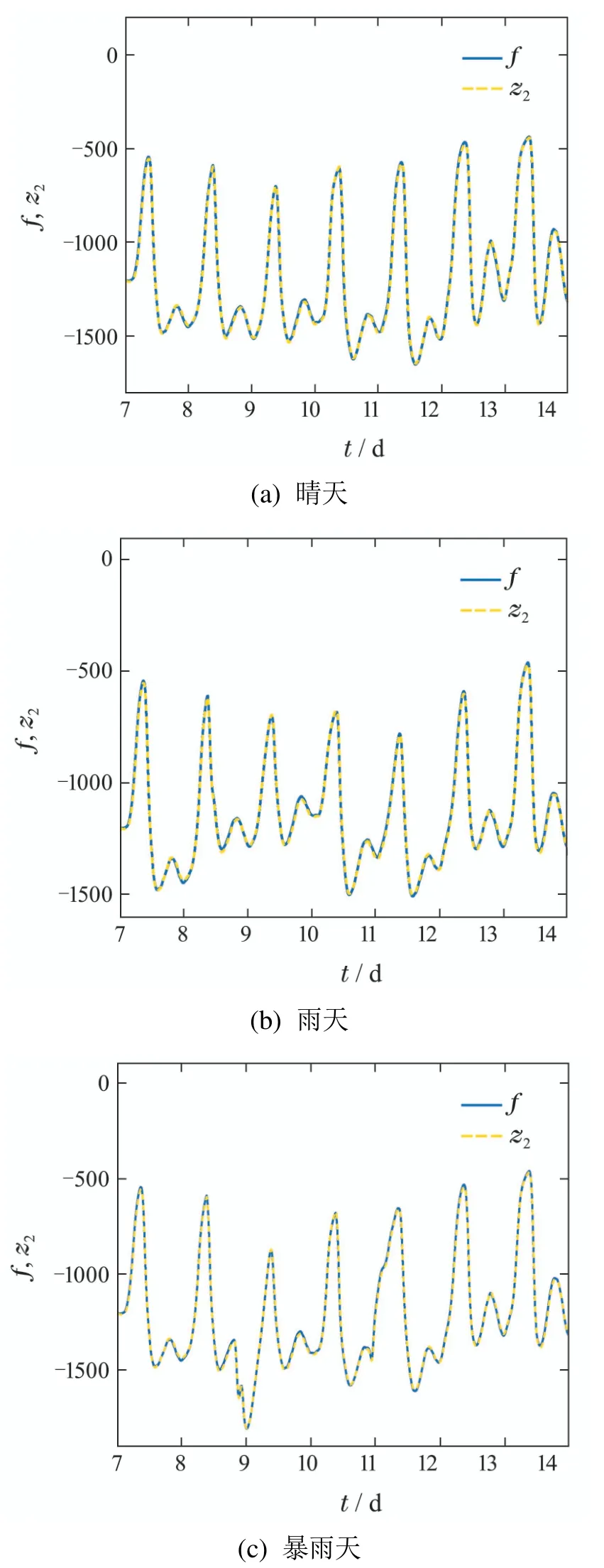
图9 3种天气下扩张状态观测器的总扰动估计效果Fig.9 Total disturbance estimations of ESOs under three weather conditions

5 结论

针对污水处理过程的溶解氧浓度控制问题,考虑污水处理受多源干扰影响、难以获得准确的数学模型的特点,本文提出了基于扩张状态观测器和滑模控制的复合抗扰控制策略.扩张状态观测器估计系统总扰动并通过控制律补偿,滑模控制抑制无法完全补偿的扰动,能够有效减小控制能耗、提高污水处理效果.基于国际水协会提出的污水处理过程控制性能评价模型BSM1,对比了PI,SMC,ADRC和CDRC调控溶解氧的性能指标,验证了复合抗扰控制在溶解氧浓度控制中的效果.为污水处理过程溶解氧浓度控制提供了一种可行的参考方案.