小学估算教学的误区及应对策略
——从“加法估算,先把加数四舍五入到十位”谈起
□石忠富
一、缘起

这是人教版三年级上册P18的一道题,“今天大约卖出多少根冰棍?”女儿在课本上写下了610根(如上图),从中可以看出她的估算过程:392≈390,219≈220,392+219≈390+220=610(根)。我问390+220计算起来简单吗?女儿告诉我,她觉得估算也并不是很简单的事,班上有好多同学在列竖式计算390+220。我问她为什么不把392看成400,把219看成200?估算成392+219≈400+200=600(根)不是更简单吗?我的想法遭到了女儿的否定,她告诉我她的老师规定:两个数相加,估算时先把这两个加数分别四舍五入到十位,就是对个位进行四舍五入,再相加。
“加法估算,先把加数四舍五入到十位?”这样的估算,结果毫无疑问是正确的,但是这样估算的过程简单吗?估算应该是粗略、简约地计算,上题的估算过程其实是改变数字后的精确计算。在数学学习中,这样的估算方法能体现估算什么样的价值呢?解决问题时的生命力在哪呢?
二、估算教学误区成因
(一)来自传统计算教学的影响
教材处理估算时,总是把它与口算(认为口算是笔算的基础)处于同等地位,估算情境往往放在笔算之前,用来验证笔算的正确性,让学生觉得反正要进行笔算,估不估无所谓。而学生相对擅长精确计算,对估算的作用没有真切的体验和感受,缺乏自觉估算的意识,体会不到估算在实际生活和数学学习中的价值。
(二)来自估算过程中方法的偏位
在估算教学中,教师没有领会估算教学的内涵和目标要求,再加上课堂教学时间有限,教师常常忽视让学生对估算的思考过程用语言做出解释,忽视学生对估算方法的感悟。估算教学“蜻蜓点水”,学生学而不精。
(三)来自评价模式的干扰
很多教师认为数学考试的答案是唯一的,认识停留在应试的层面上,认为估算教学必须教给学生一个统一的方法,例如,382+514,如果给学生规定估算的标准,把加数都四舍五入到十位,那么答案就统一为382+514≈380+510=890,这样学生在应试中正确率就相对较高,教学过程也简单明了,因为答案是唯一的,作业批改简单方便。
三、全面理解估算
其实估算的方法是多样的、开放的,结果也是多元的。估算没有唯一标准,只要在某个区间内能体现问题解决的价值,那就是合理的。国内外对估算有着不同的界定,罗增儒教授将估算定义为粗略的计算,实质上是一种快速的近似计算,它的基本特点是对数值进行扩大或缩小,从而对运算结果确定一个范围或做出一个估计,Dowker将其定义为在没有精确计算或在精确计算之前对一些算术问题做一个合理的猜测。
本文中所指的估算是未经过精确计算对问题提出粗略答案的一种估计,是心算、数概念和算术计算技巧之间相互作用的过程。
但粗略不是随意,它要求计算过程简单而快速。Reys等人(1987)说过,“估算可以使我们判断一个经由粗略计算得到的答案的合理性”。“先把加数四舍五入到十位”的估算方法不是不行,但得考虑这种估算是否繁杂,很显然,这种估算就是因为题目要求估算而增加的过程,实际是为估算而估算。
[案例]
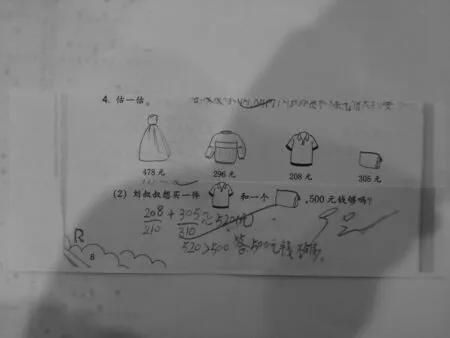
这是人教版三年级上册《数学作业本》P8的一道题,第(2)小题,要求学生通过估一估判断500元钱够不够买一件上衣和一个包。这个问题的正解是:把208看成200(估少),305看成300(估少),208+305≈200+300=500(元),因为200+300<208+305,也就是估少后,计算的结果是500,所以500元钱是不够的。采取整百数估算,整个过程简单快速,学生也容易理解,估算解决问题的优势非常明显。上图是女儿作业本的截图,可以看出她遵循“先把加数四舍五入到十位然后再相加”的方法,远没有取整百数作近似数计算起来简单快速。
另外,女儿的解答中还有一个明显的错误,把208看作210(估大),把305看成310(估大),两个加数都被估大,那么最后的结果肯定被估大,估大了结果以后又怎么能判断500元够不够呢?估小不够肯定不够,估大不够就无法判断了。
所以作为数学教师,应该要清醒地认识到估算的重要意义,不要为估算而估算。
四、走出估算教学误区的策略
估算是估和算的过程,是具有推理和猜想的心理活动,是一种开放的计算活动,它没有通用的模式和方法,其合理性取决于问题的背景和要求。估算的结果是不唯一的,不同的精确度要求使用不同的估算策略,不同的估算策略自然导致不同的估算结果,对于结果孰优孰劣,必须同时考虑误差的大小和计算的繁简。
那么,如何走出估算教学的误区呢?
(一)增强估算意识
教师要提高估算教学对于促进学生形成良好数感重要性的认识,在实际行动上加强估算教学。
日常教学中需要用到估算的地方很多,教师要做一个有心人,寻找契机。可通过观察、分析、交流估算方法、技巧等途径,让学生感受估算的乐趣,体验估算的便捷,凸显估算的价值。
[案例]
学生在笔算“735÷7”时出现了三种不同的答案。

哪个答案是正确的呢?学生进行了激烈的讨论,其中有位学生果断地认为答案(3)是错误的,因为735÷7的商应该是100多,不可能是15,如果商是15的话,那么被除数应该是100多。另一个学生说,答案(2)肯定也是错误的,如果商是170的话,那被除数要接近1000。这里估算是进行判断的一个重要策略,这种估算教学有过程,有探究,有交流,有需要。学生经过思考,将笔算、估算、验算有机结合,相互作用。与笔算相比,估算快速,优势明显。
(二)加强方法指导
估算是一种开放的创造性活动,往往带有很多不确定因素。这就要求学生明白,什么时候估算是合理的,可行的;如何根据条件确定估算的精确度;如何提取主要因素,忽略不重要数据,这一切都需要结合实际需要,灵活选择。
1.取整估算
取整估算是教材比较强调的一种估算方法,是一种有用且有效的策略。取整包括取整十数、取整百数、取整千数等,也包括保留最高位法。小数也同样可以采用取整法。
[案例]
a.估算:905-688。取整十数:905-688≈910-690=220;取整百数:905-688≈900-700=200。这里估算的过程所运用的是一个取整思维,不管采用哪一种方法得到的结果都是正确的。
b.估算:9.21+10.07。取一位小数:9.21+10.07≈9.2+10.1=19.3;取整数:9.21+10.07≈9+10=19。虽然是小数的估算,但是这里依然属于取整思维。
2.口诀估算
口诀估算,就是直接运用乘法口诀去估算结果的一种方法,在乘法和除法的估算过程中是比较多见的。
[案例]
a.估算:67×8。看到这样的题目,马上想到乘法口诀,七八五十六,估算过程可以写作:67×8≈70×8=560。
b.估算:346÷8。和上面的乘法一样,运用口诀:四八三十二,346÷8≈320÷8=40,这里需要考虑的是,不要把346取近似数350,否则估算起来就有很大的麻烦。
c.估算:258×41。如果将两个因数四舍五入到十位,那么估算的过程就是258×41≈260×40=10400,但仔细研究会发现这两个因数是一个特殊组合,258不一定要估成260,可以取近似数250,那样的话算起来会更加方便,估算的过程就可以写成250×40≈10000,这样的估算,其实也可以算作是口诀估算的一种。当然,258×41也可以用取最高位法把258估计成300,41估计成40,估算的过程又可以写成258×41≈300×40=12000。
估算结果会因估算的方法不同而不同,只要估算的过程是合理的,估算就是正确的,它能很好地培养学生的数感。
3.引入中间量估算
引入中间量来估算,多用于“比较数的大小”。
[案例]
引入中间量来估算,其实还包括取平均数估算,如:54+48+47+51+54≈(),仔细观察发现,这几个加数都和50很接近,可以用50作为这组数的基准数,那么估算的过程就可以写作54+48+47+51+54≈50×5=250。这个中间量50很重要,它是这组数的近似数,所以估算的时候就以这个数为基准数,利用乘法口诀五五二十五,把这五个数的和的近似数求出来了。
4.化成分数或小数估算
有时候取整数后计算并不容易,化成小数或分数反而更加方便。
[案例]
估算:63.2×0.33。估算除了要快速粗略估计以外,它的估值也有一定的范围,看这组数的特征,63.2把小数部分的2去掉刚好是63,是3的倍数,而很接近,所以根据经验,可以把估算的过程写成
估算的方法有很多,使用的时候往往相互融合。
(三)重视能力培养
估算不仅在解决实际问题上表现出价值,对培养学生的数学意识,发展学生的数学思维也有重要意义。
[案例]
“水上乐园门票8元一张,39位师生购买门票大约需要带多少钱?”这是用估算的方法解决实际问题,学生往往有以下三种答案。
(1)39×8≈40×8=320(元)
(2)39×8≈39×10=390(元)
(3)39×8≈40×10=400(元)
三种估算的结果虽然不同,但都是合理的,因为它符合估算的本质意义:在一定范围内,快速估计。但是这里涉及学生对日常问题的判别能力,首先是带的钱足够买所有的门票,其次是带的钱与准确数接近。所以从估算的结果可以看出学生的计算能力、评估判断能力、对数的感知能力,是多种思维能力的结合。
总之,估算是一项数学的基本技能,教师要努力将估算教学内化为一种自觉的意识,努力挖掘教材中隐含的估算资源,并为学生搭建估算平台,让学生的估算策略合理,多样灵活。

