单输入单输出系统离散积分滑模预测控制
刘 邱,赵东亚
(中国石油大学(华东) 新能源学院,山东 青岛 266580)
滑模控制最早出现于20世纪50年代,由Utkin提出[1].经过几十年的发展,滑模控制已成为一个相对独立的研究分支,广泛适用于线性和非线性系统、确定和不确定系统以及连续和离散系统等[2].随着现代计算机技术的发展,越来越多的场合利用计算机来控制,因此,离散滑模控制的研究得到了更多的关注和发展.普通的滑模控制在跟踪轨迹时,如果有外部扰动,易产生稳态误差,难以达到预期的性能指标.针对上述问题,Slotine等[3]提出了一种积分滑模控制器策略,通过该积分非线性滑模面削弱了系统抖振并减小了系统误差.文献[4]提出了一种可以更加自由地选取滑模面参数的一般形式积分滑模面.文献[5]提出了一种新的积分滑模控制方法,解决了对象的局限性问题,并将其成功应用于最小相位系统和非最小相位系统.因为积分滑模良好的控制表现,越来越多的学者投身于积分滑模的研究.此外,积分滑模控制器的设计也得以推广到带有匹配以及非匹配不确定性连续或离散系统中[5-7].相对一般滑模控制而言,在积分滑模面中,系统具有和状态空间一样的维数.在设计积分滑模控制器时,可以通过合理设计状态初始值,保证系统的状态轨线总是处于滑模面上,从而消除了不具备鲁棒性的趋近阶段,保证了系统的整体鲁棒性[8].
预测控制是一种在工业应用中发展起来的一种控制技术,其控制的3项基本组成为:预测模型、滚动优化和反馈校正[9],即通过状态空间、阶跃响应这样的预测模型得到未来的动态行为,对未来的输出进行预测以及在线优化,对未来的误差做出预测和补偿[10].预测控制的优点在于对模型的要求不高,简化了系统建模的工作,并且滚动优化的策略保证了系统的动态特性.近年来,研究人员在预测控制在理论及应用方面都取得了极其显著的成果,突破了早期的框架,与鲁棒控制、滑模控制、自适应控制等相结合,形成了更为先进的控制策略[11].文献[12]将预测控制和滑模控制结合,以系统名义模型为预测模型,将滚动优化、反馈校正的思想引入离散滑模控制器的设计中,既削弱了抖振又加强了鲁棒性.文献[13]将滑模控制与非线性模型预测控制结合,利用切换函数使滑动模态渐进稳定,在有限预测时域的基础上,对切换函数施加等式约束.结果显示,该方法结合了预测控制处理约束和滑模控制对干扰不变性的优点.
考虑到滑模控制与模型控制的特点,本文将离散积分滑模控制与模型预测控制结合,设计了一种离散积分滑模预测控制器,所提出的控制算法具有积分滑模控制的强鲁棒性,削弱了预测控制的超调,还解决了滑模控制不能处理约束的问题.
1 离散积分滑模设计
考虑一个不确定离散系统
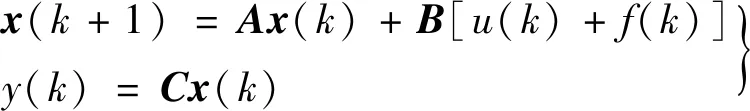
(1)
式中:x(k)∈Rn×1为状态向量;u(k)为控制输入;A∈Rn×n,B∈Rn×1可控;C∈R1×n;f(k)为输入的干扰.
离散积分滑模设计:
σ(k)=Gx(k)-Gx(0)+b(k)
(2)
b(k)=b(k-1)-
[GBu0(k-1)+GAx(k-1)]
(3)
式中:σ∈R,b∈R,b(0)=0,G∈R1×n.
由式(2)和(3)可得
σ(k+1)=
Gx(k+1)-Gx(0)+b(k+1)
(4)
b(k+1)=
b(k)-[GBu0(k)+GAx(k)]
(5)
将式(5)代入式(4)得
σ(k+1)=Gx(k+1)-Gx(0)+b(k)-
[GBu0(k)+GAx(k)]
(6)
将等式(6)变形
σ(k+1)=Gx(k+1)+Gx(k)-
Gx(0)+b(k)-Gx(k)-
[GBu0(k)+GAx(k)]
(7)
由积分滑模性质可知
σ(k+1)=σ(k)=0
(8)
则式(7)可化为
(9)
将u0(k)写为
u0(k)=u1(k)+u2(k)+u3(k)
(10)
式中:u1(k)由预测控制设计;u2(k)设计为状态反馈的形式;u3(k)为克服干扰项;I为单位矩阵.
(11)
式中:K∈R1×n,η∈R.这里状态反馈增益K和滑模控制增益不同.
2 预测控制设计
基于模型预测控制系统未来的动态,默认系统全部状态可测,将状态空间模型(式(1))改写为增量模型
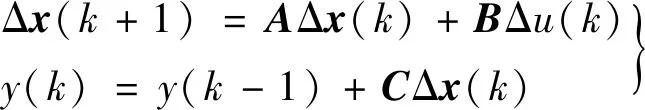
(12)
式中:
Δx(k)=x(k)-x(k-1)
Δu(k)=u(k)-u(k-1)
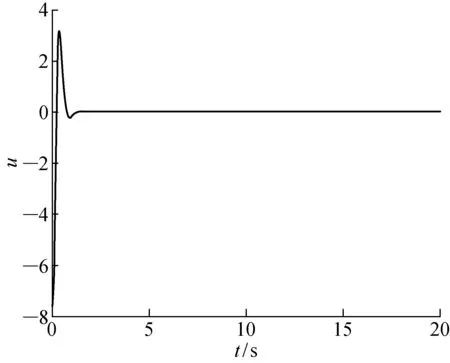
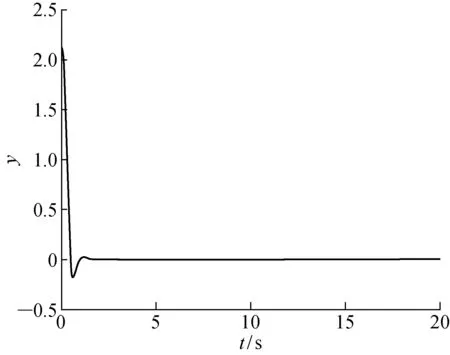
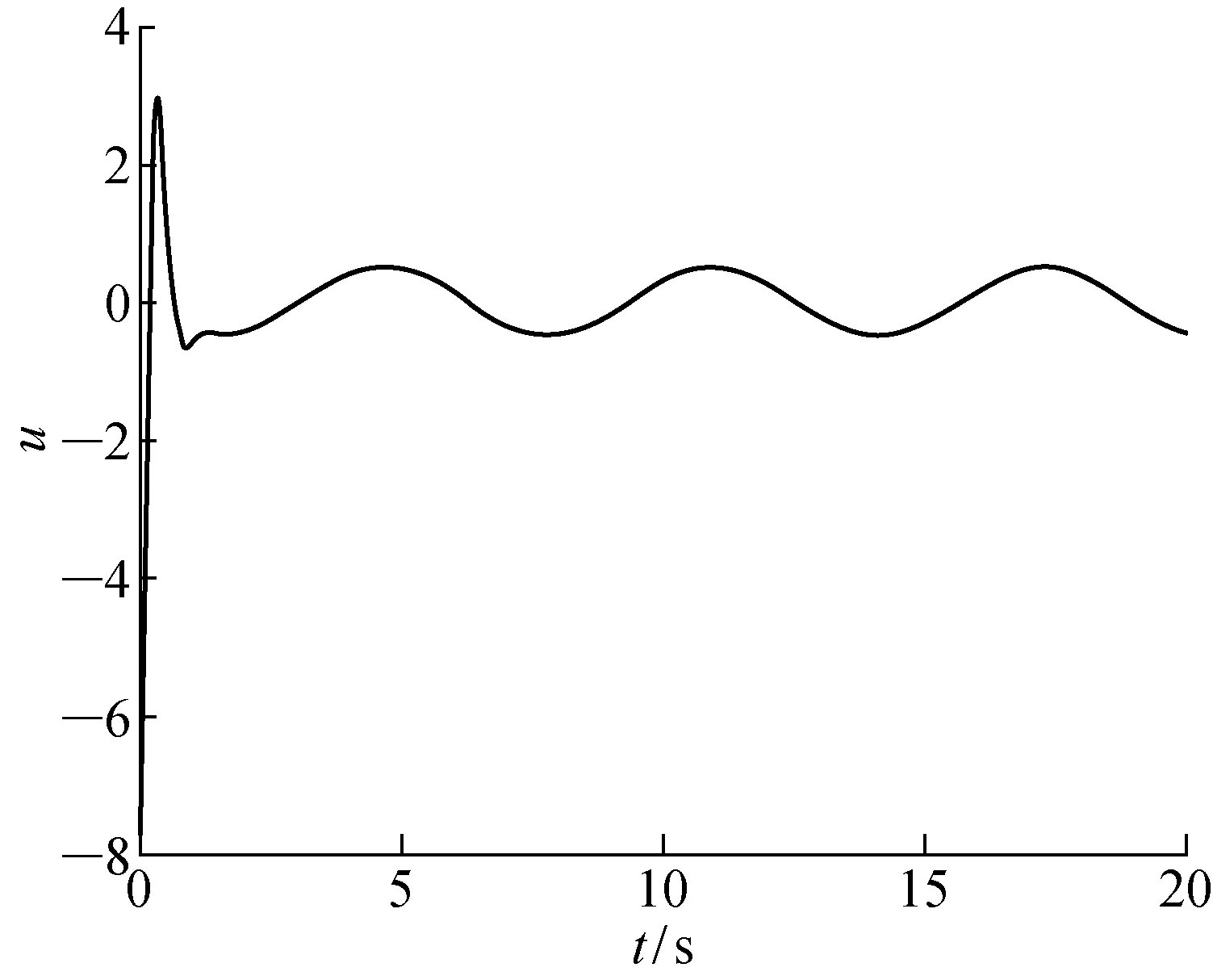
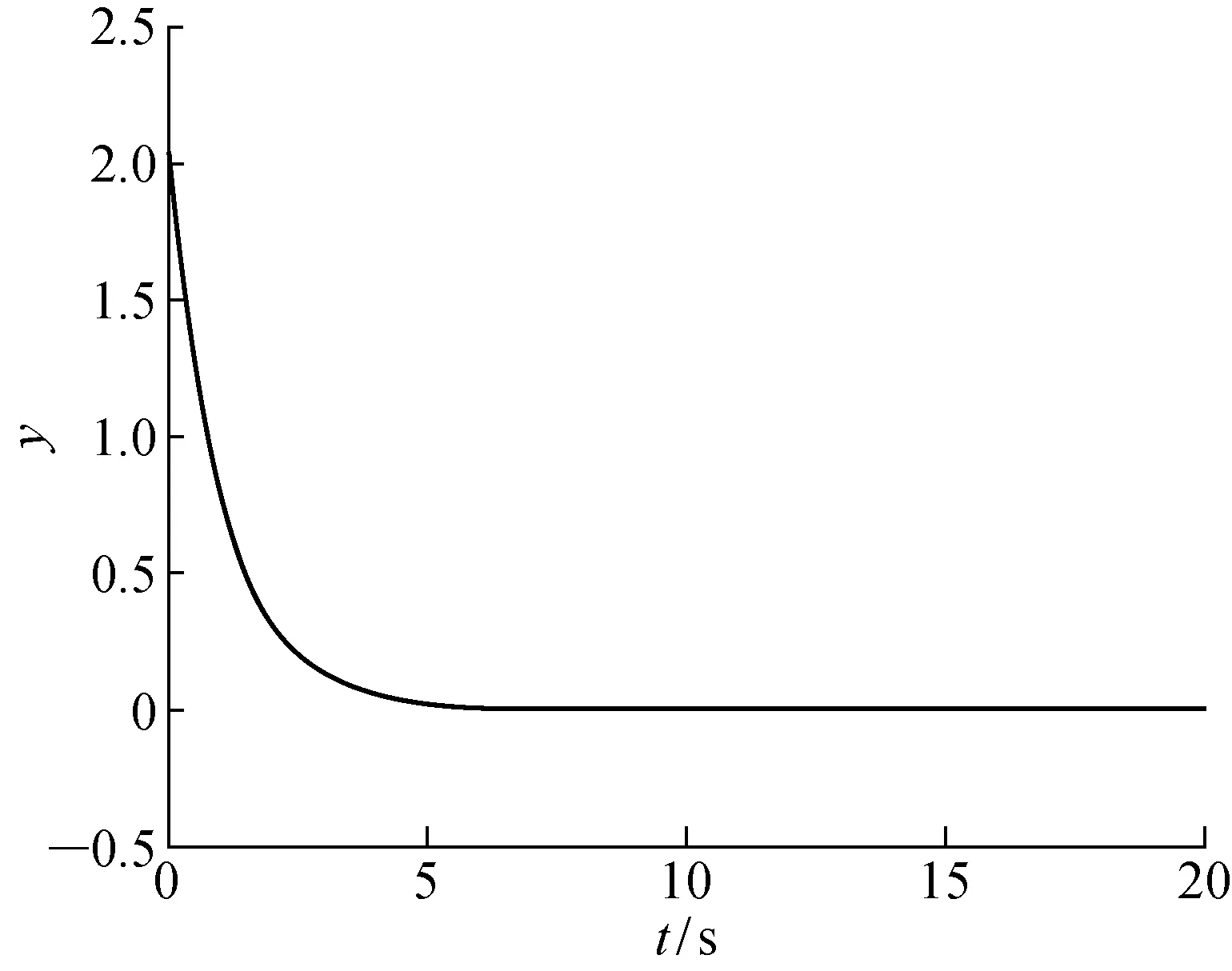
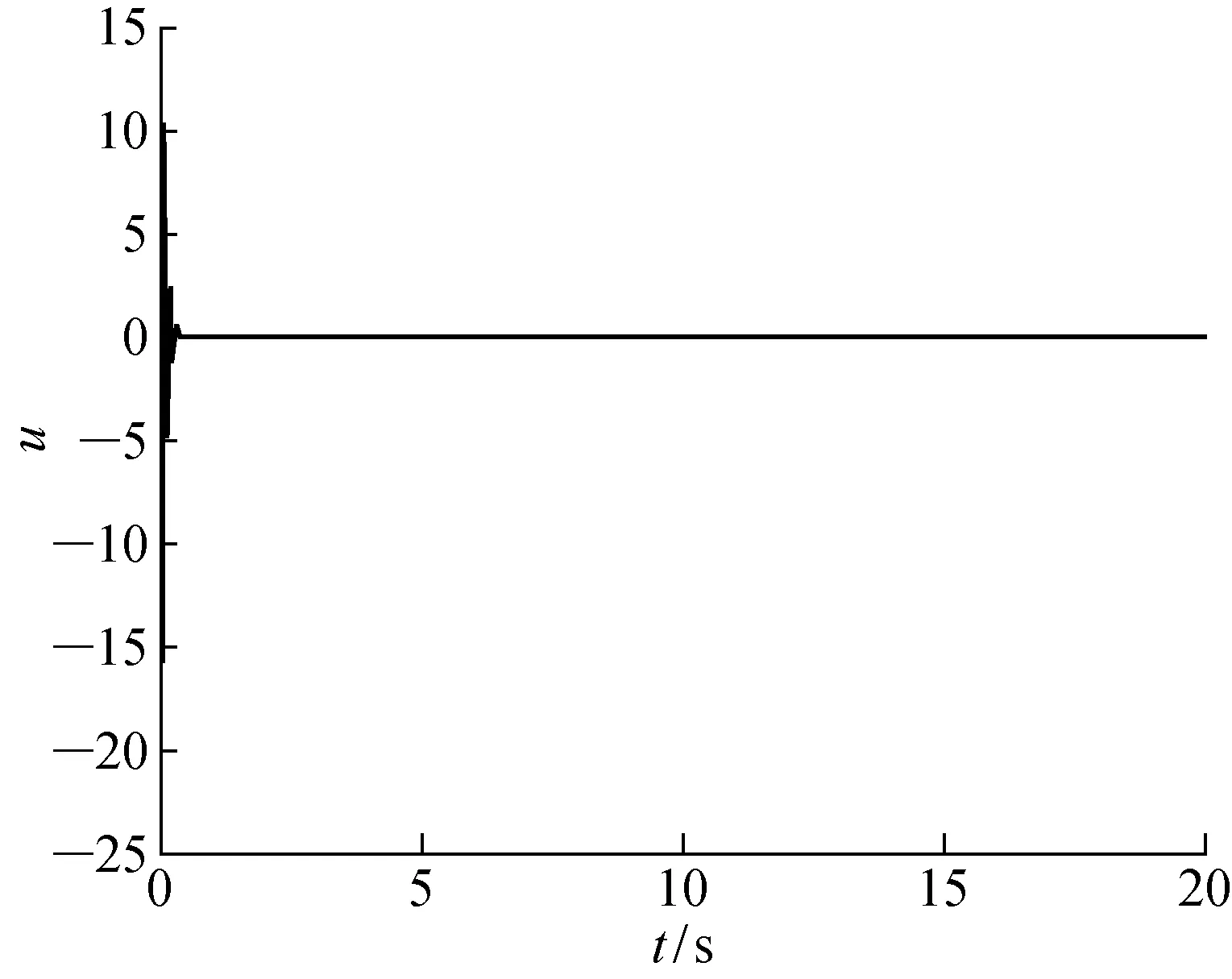
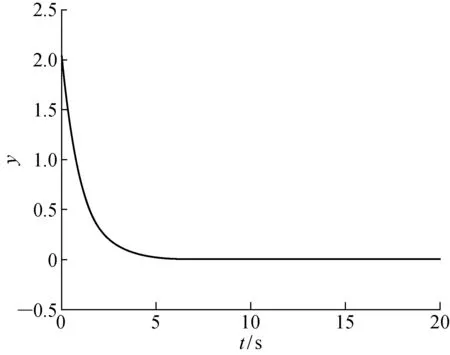
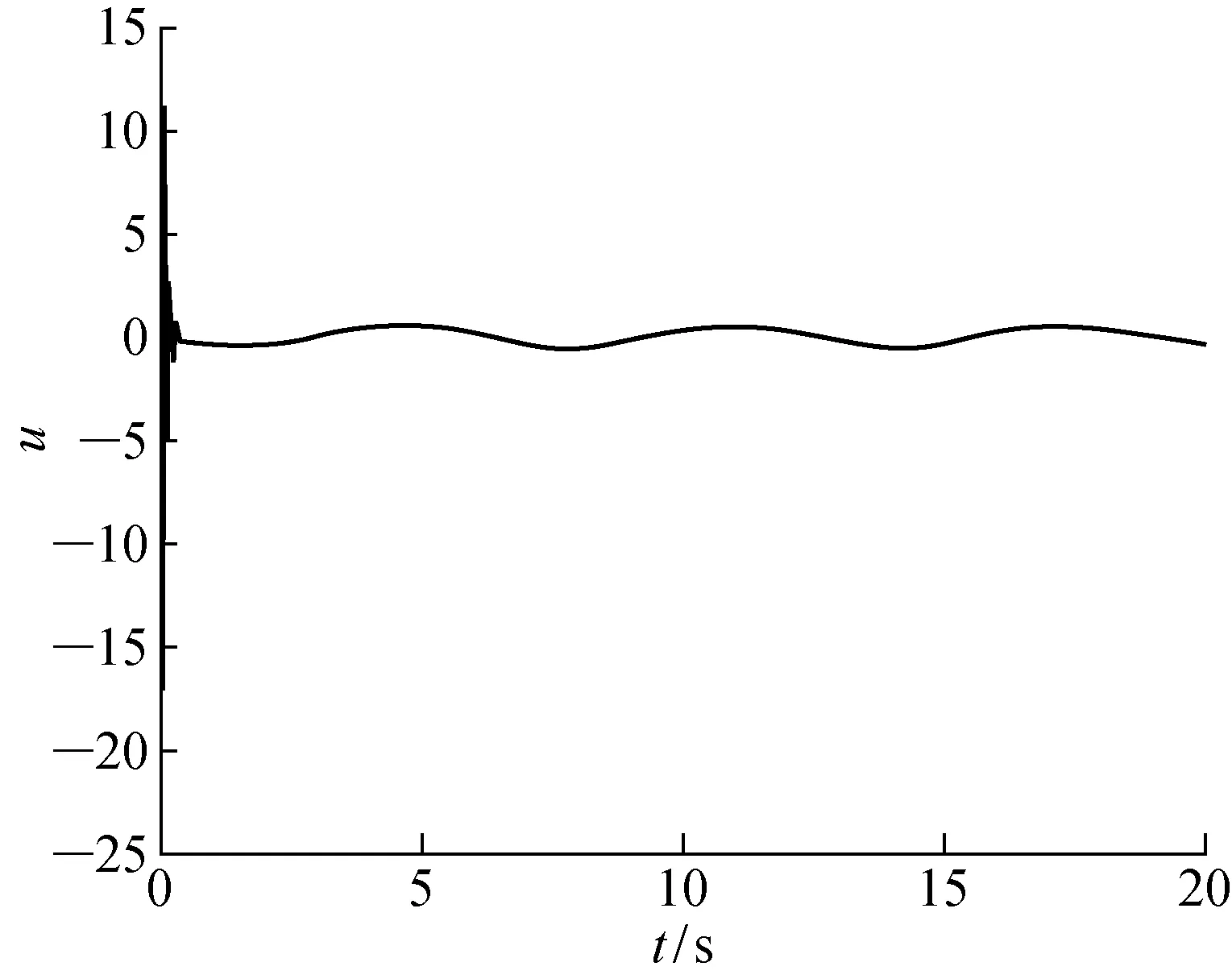
预测控制的原理首先是以最新测量值为初始条件的,并基于模型(式(1))来预测未来系统状态.设控制时域为m,预测时域为p,且m 假设1在控制时域以外,控制量不变,即Δu(k+i)=0,m≤i 假设2可测干扰在k时刻后不变,即Δu(k+i)=0,1≤i 在当前时刻k,可以预测未来p个时刻的状态增量: Δx(k+1|k)=AΔx(k)+BΔu(k) Δx(k+2|k)= Δx(k+1)+BΔu(k+1)= A2Δx(k)+ABΔu(k)+BΔu(k+1) ⋮ Δx(k+p|k)= Δx(k+2)+BΔu(k+2)= ApΔx(k)+Ap-1BΔu(k)+ Ap-2BΔu(k+1)+…+BΔu(k+p-1) 同理,可以预测未来p个时刻的输出为 y(k+1|k)=CΔx(k+1|k)+y(k)= CAΔx(k)+CBΔu(k)+y(k) y(k+2|k)=CΔx(k+2|k)+y(k+1|k)= (CA2+CA)Δx(k)+y(k)+ (CAB+CB)Δu(k)+CBΔu(k+1) ⋮ y(k+p|k)= CΔx(k+p|k)+y(k+p-1|k)= 将预测输出(p步)以及输入(m步)写成向量的形式: (13) (14) 由此可以得到预测未来p步输出的预测方程 Y(k+1|k)= SΔx(k)+Iyy(k)+QΔU(k) (15) 式中: Q= 为求解控制律,选取目标函数如下: (16) 式中:r为参考轨迹.为方便求解,将式(16)写成矩阵向量形式 J=‖Γy(Y(k+1|k))- R(k+1)‖2+‖ΓuΔU(k)‖2 (17) 式中: Γy=diag(Γy,1,Γy,2,…,Γy,p) Γu=diag(Γu,1,Γu,2,…,Γu,m) 为方便求解,定义辅助变量 (18) 则目标函数变为 J=ρTρ (19) 将式(13)和(14)代入式(18)得 ρ= Φz-Ω (20) E(k+1|k)= R(k+1)-SΔx(k)-Iyy(k) (21) 求解问题在于使目标函数最小化,即 minρTρ (22) 对式(22)求导: (23) 求得极值解为 z*=(ΦTΦ)-1ΦTΩ (24) 二阶导数 (25) 所以z*为目标函数取得最小值的解. 则得到k时刻的最优控制序列为: ΔU*(k)= (26) 根据模型预测控制的原理,只有最优控制序列的第一个元素作用于系统,即: (27) 为简化形式,定义控制增益为 (28) 则控制增量为 Δu(k)=KmpcE(k+1|k) (29) 可得控制律: u(k)=u(k-1)+Δu(k) (30) 考虑系统的增量模型: Δx(k+1)=AΔx(k)+BΔu(k) (31) 推导闭环系统表达式,将式(21)和(28)代入式(29)可得 Δu(k)= Kmpc[R(k+1)-SΔx(k)-Iyy(k)]= KmpcR(k+1)-KmpcSΔx(k)-KmpcIyCx(k) (32) 将式(32)代入(31)得 Δx(k+1)= AΔx(k)+BKmpcR(k+1)- BKmpcSΔx(k)-BKmpcIyCx(k)= (A-KmpcS)Δx(k)+ BKmpc[R(k+1)-IyCx(k)] (33) 由自动控制稳定性条件可知,如果矩阵(A-KmpcS)所有特征值都位于单位圆内,则闭环系统(式(33))是名义渐近稳定的. 研究如下的SISO系统: (34) 当采样时间T=0.01 s时, f(k)=0.5sin(kT) (35) (36) 预测时域p=30,控制时域m=4, 单纯的预测控制仿真结果如图1~4所示:单纯的预测控制能够使系统在有限时间内稳定,但面对干扰系统控制不太平稳,存在超调现象,控制输入的波动也比较大. 图1 纯预测控制无干扰的输出Fig.1 Output of predictive control without disturbance 图2 纯预测控制无干扰的输入Fig.2 Input of predictive control without disturbance 图3 纯预测控制有干扰的输出Fig.3 Output of predictive control with disturbance 图4 纯预测控制有干扰的输入Fig.4 Input of predictive control with disturbance 图5 滑模预测控制无干扰的输出Fig.5 Output of sliding mode predictive control without disturbance 图6 滑模预测控制无干扰的输入Fig.6 Input of sliding mode predictive control without disturbance 图7 滑模预测控制有干扰的输出Fig.7 Output of sliding mode predictive control with disturbance 图8 滑模预测控制有干扰的输入Fig.8 Input of sliding mode predictive control with disturbance 滑模控制和预测控制算法都是工业应用中比较成熟的控制算法.本文利用滑模控制对干扰的鲁棒性和预测控制能够利用丰富的动态信息多步预测输出状态的优点,提出了一种积分滑模预测控制算法.该方法结合了两种控制算法的优点,具有控制平稳、超调量小的优点,为处理约束问题和提高控制鲁棒性提供了一种新的思路.
3 稳定性分析
4 仿真研究
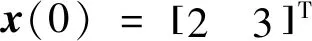

5 结语

