基于径向点插值方法的柔性螺旋桨气动弹性模拟

张 宇，王晓亮

(上海交通大学 航空航天学院，上海 200240)

流固耦合问题广泛存在于航空航天、船舰和能源等领域[1-3].气动弹性问题的本质与流固耦合问题一致，常见于飞行器设计领域，主要涉及机翼颤振和螺旋桨变形等[4-5].作为常规飞行器(推进器)中的重要分支——螺旋桨动力飞行器(推进器)在航空(航海)领域始终扮演着关键角色.螺旋桨作为早期的动力系统，因其在低速时具有高推力、低能耗等优点，被广泛使用在平流层飞艇、运输机和倾转旋翼机上[6-7].典型的飞行器有A400M运输机、C-130运输机、运12、AG600水陆两用飞机、V-22倾转旋翼机等.普通螺旋桨一般由合金材料制造，故在设计时把螺旋桨桨叶视为刚体而忽略在运行过程中可能发生的变形.但随着飞行器的载荷能力和机动性能的不断提高，普通的合金材料对高强度气动载荷和周期性疲劳振动的承受能力会大大降低.因此，新型的碳纤维材料逐渐进入了人们的视野[8].相较于传统的金属螺旋桨，碳纤维材质的螺旋桨具有更好的抗疲劳性，能在一定程度上降低整机重量，提高有效荷载能力.但由于粘接和复合工艺的限制会造成弹性模量较低，在运转时易发生变形，此时的螺旋桨推进性能将会发生改变.如果忽略气动弹性，往往又会造成设计点的偏移，使真实情况与预期有较大的偏差.因此，在对柔性碳纤维螺旋桨进行推进性能预测时，有必要考虑材料的气动弹性效应.

在针对螺旋桨气动弹性问题的研究方法上，Sodja等[9]结合叶素动量理论和非线性梁理论，建立了柔性螺旋桨的气动弹性简化模型，并预测了前掠、后掠和平直型螺旋桨的推进性能结果.Hsiao等[10]耦合了可压/不可压流体求解代码和有限元固体求解代码，对多层复合材料螺旋桨的推进性能进行了研究，最后给出了合适的铺陈方式以提高推力.Zhang等[11]依托ANSYS Workbench软件中的System Coupling平台，研究了在流固耦合作用下夹层复合材料螺旋桨的推进效率和结构响应.Das等[12]使用一阶切应变理论和雷诺平均Navier-Stokes(RANS)方程研究了全尺寸多层粘合弯扭螺旋桨的推进特性.王建等[13]采用面元法与有限元法相结合的流固耦合分析方法对碳纤维螺旋桨进行了水动力性能分析，并借助iSIGHT软件构建起基于响应面近似模型碳纤维螺旋桨的多目标优化策略.娄本强等[14]分别使用直接耦合数值计算和瞬态激励实验方法，研究了某型螺旋桨叶片在空气中和浸入静水域中的固有流固耦合振动特性.

从上述文献可见，虽然现有研究已经建立起了关于螺旋桨气动弹性的分析技术，但已有的研究方法一般是通过简化的理论方法将流场和位移场方程耦合并求解，这种方式在应用对象上有一定的局限性，对于复杂的工况不能完全反映其流场情况.此外，通过封装好的平台实现耦合过程中的数据传递，容易导致数据不透明，降低了信息提取的自由度.

本文借助成熟的计算流体力学(CFD)/计算固体力学(CSD)求解器分别求解流场和位移场，CFD/CSD模块彼此独立，可操作性较强，便于数据信息的提取.应用无网格的径向点插值方法(RPIM)完成固体网格节点朝流体网格节点的位移传递[15].结合位移传递矩阵和虚位移原理，生成节点力传递矩阵，该方法能保证数据在传递中力、力矩和能量的守恒.在动网格方面，采取Delaunay映射法进行流场网格更新，相较于传统的弹簧光顺等方法，Delaunay映射法具有更高的计算效率和稳健性，适用于任意拓扑类型的网格[16].

1 几何模型

1.1 螺旋桨几何模型

螺旋桨模型的基础剖面翼型为Clark Y，通过片条理论获得螺旋桨叶片的气动响应，再由遗传算法优化获得最佳的螺旋桨设计参数.该螺旋桨的直径Dp为4.6 m，桨毂直径Dg为0.92 m.由于桨毂对叶片的变形以及对螺旋桨周围的流场结构影响较小，为简化问题去除桨毂结构，最终获得的外形如图1所示.

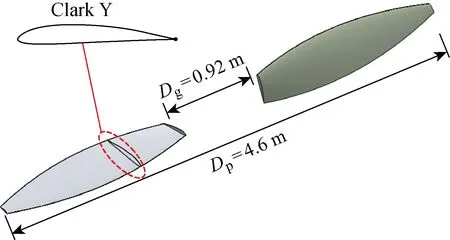
图1 螺旋桨几何外形示意图Fig.1 Schematic diagram of propeller geometry

1.2 CFD计算域模型

CFD计算域模型如图2所示，整个模型包括一个旋转域和一个静止域，FLUID_PROP为包含螺旋桨PROP的旋转域，FLUID为静止域.计算域尺寸如图3所示.计算域入口Inlet到旋转域FLUID_PROP的距离为10Dp，旋转域FLUID_PROP到出口Outlet的距离为30Dp，螺旋桨中心与远场壁面的距离为8Dp，旋转域FLUID_PROP的直径为1.5Dp，旋转域FLUID_PROP沿来流方向的尺寸为0.5Dp.旋转域FLUID_PROP与静止域FLUID之间的交界面类型为Interface，通过插值进行数据交换，各边界名称与类型统计如表1所示.

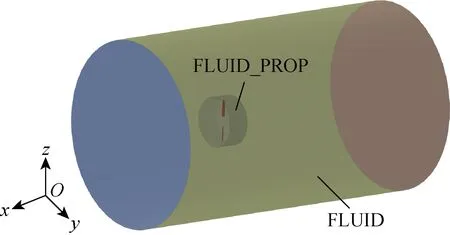
图2 流体计算域Fig.2 Fluid computational domain

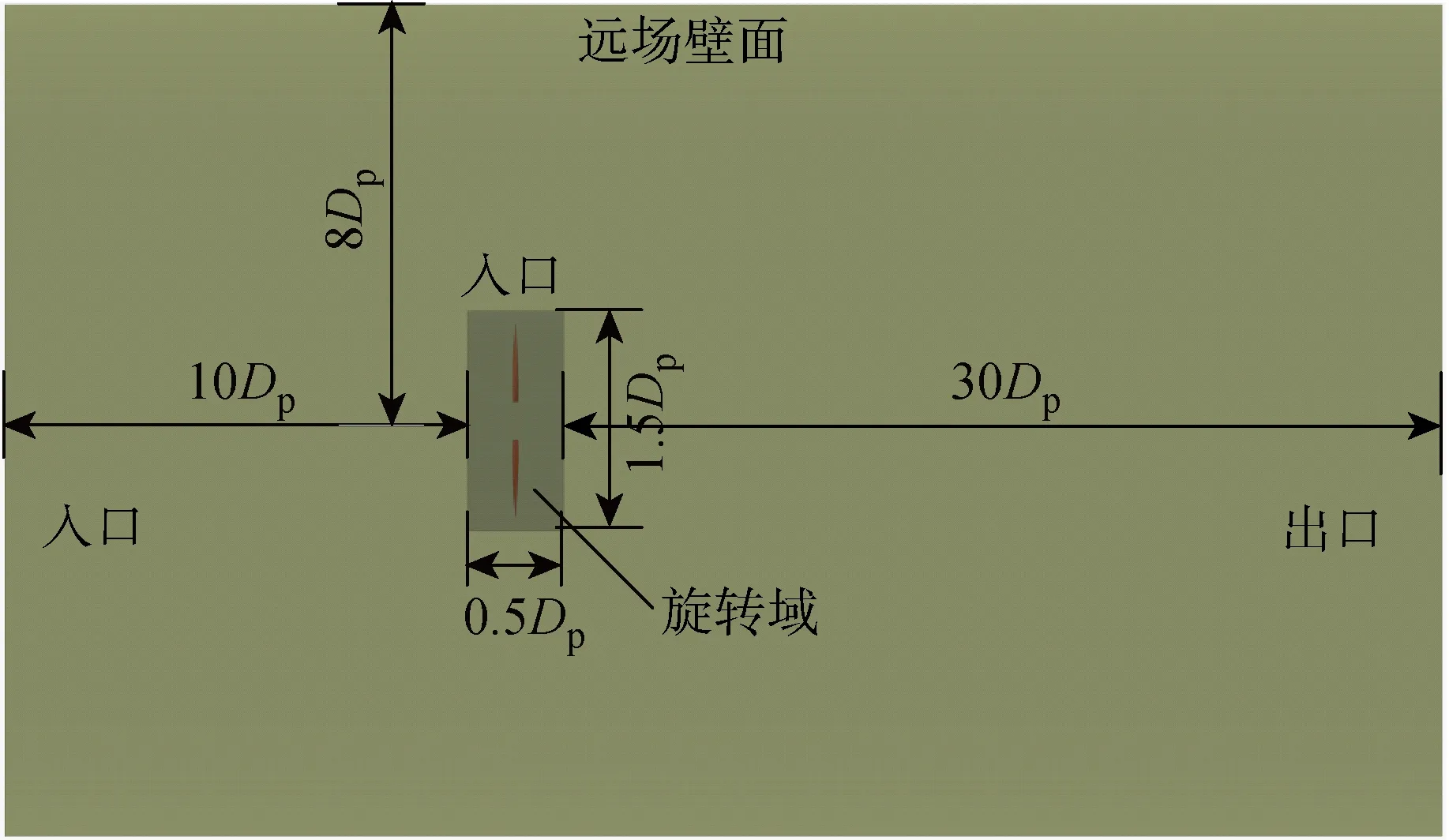
图3 计算域尺寸Fig.3 Computational domain size

表1 边界条件分类Tab.1 Classification of boundary conditions

2 计算方法与可靠性验证

2.1 Delaunay映射方法

流场网格更新通过Delaunay方法实现，该方法具有很高的稳健性，避免了求解大型矩阵的高耗时缺点.Delaunay四面体如图4所示.流体域内任意一个网格节点P在Delaunay四面体ABCD的位置由体积坐标(e1,e2,e3,e4)唯一确定：

图4 Delaunay四面体Fig.4 Delaunay tetrahedron

(1)

(2)

(3)

(4)

(5)

(6)

显然对于体积坐标有：

(7)

因此，当物面网格节点发生位移u后，流体域内网格节点的位移可由下式获得：

(8)

使用Delaunay映射方法对NACA0012二维网格进行变形的结果如图5所示.翼型表面的运动方式为ΔY=-0.1sin(2πX)，X、Y为无量纲长度.变形前流场网格的最小正交质量为0.445，变形后流场网格的最小正交质量为0.124.从变形前后的翼型周围网格分布来看，Delaunay映射方法能较好地完成贴体网格及流场网格的更新.

图5 NACA0012二维翼型网格变形Fig.5 NACA0012 2D airfoil grid deformation

2.2 可靠性验证

采取成熟的商业软件ANSYS Fluent©和Abaqus©分别求解气动载荷和结构位移.流场网格划分工具为ICEM CFD，在静止域FLUID采用结构网格剖分，在旋转域FLUID_PROP内使用非结构网格填充，在螺旋桨周围进行网格加密，所获得的最终网格如图6所示.网格单元总数为 2 134 807，旋转域内节点数为 304 975，单片桨叶表面节点数为 13 535.考虑到螺旋桨周围流场存在强烈的流动分离情况，湍流模型选取k-ω剪切应力输运(SST)模型.同时鉴于螺旋桨运行时的动平衡特点，采取多重参考系(MRF)方法求解旋转流场，该方法通过求解准静态的RANS方程获取旋转域内的流场信息.MRF方法的主要思想是将螺旋桨相对于静止流场的运动转变为旋转流体相对于静止螺旋桨的运动，通过隐式交界面进行旋转域与静止域之间的数据交换，以保证各通量守恒[17].尽管该方法是一种近似处理，与较真实的瞬态方法有一定的差异，但对螺旋桨的流动预测依然是有效的，且所需计算的资源较瞬态方法低很多[18].

图6 螺旋桨周围流体域网格Fig.6 Fluid grids around propeller

为验证本文所提计算方法CFD_MRF的可靠性，在此选取某三叶螺旋桨缩比模型进行风洞试验分析，该三叶螺旋桨的实物模型如图7所示.实验时的当地大气压为9.31×105Pa，实验风洞温度为298 K(25 ℃)，来流风速为22 m/s，转速设置为 3 186、3 536、3 886、4 236、4 586、4 936、5 086、5 236 r/min.上述工况下的推力和扭矩的变化曲线如图8和9所示.其中：F为螺旋桨推力；M为螺旋桨扭矩；n为螺旋桨转速；EXP表示风洞实验.由图8和9可知，CFD_MRF方法与实验获得的结果相近，推力和扭矩的平均误差分别为5.94%和5.90%，且变化趋势保持一致.该算例表明所提数值方法能够较好地模拟螺旋桨的真实气动效应.

图7 三叶螺旋桨实物图Fig.7 Picture of three-bladed propeller

图8 CFD方法与风洞实验所获得的推力对比Fig.8 Comparison of thrusts between CFD and wind tunnel experiment

图9 CFD方法与风洞实验所获得的扭矩对比Fig.9 Comparison of torques between CFD and wind tunnel experiment

螺旋桨由碳纤维复合材料构成，蒙皮铺层采用3621碳布预浸料(平纹布0°/90°)、M40JB(单向带)混合铺层形式.腹板铺层采用3621碳布预浸料铺层形式，其密度为 1 600 kg/m3，弹性模量近似取为70 GPa，泊松比为0.3，采取C3D8R单元进行固体网格剖分.为了消除网格因素带来的误差，通过改变螺旋桨翼型弦向网格份数和展向网格份数形成稀疏、粗糙、中等和精细4种密度等级的固体网格，4种网格的信息如表2所示.在螺旋桨叶片表面施加均布压力，并比较其变形结果.Abaqus网格无关性分析如图10所示.其中：ξp为螺旋桨叶片无量纲径向位置；ux为螺旋桨叶片尾缘在x方向上的位移.由图10可知，中等密度的网格已经能很好地满足计算精度的要求.

表2 固体模型网格参数(单个螺旋桨)Tab.2 Parameters of meshes in solid model (single propeller)

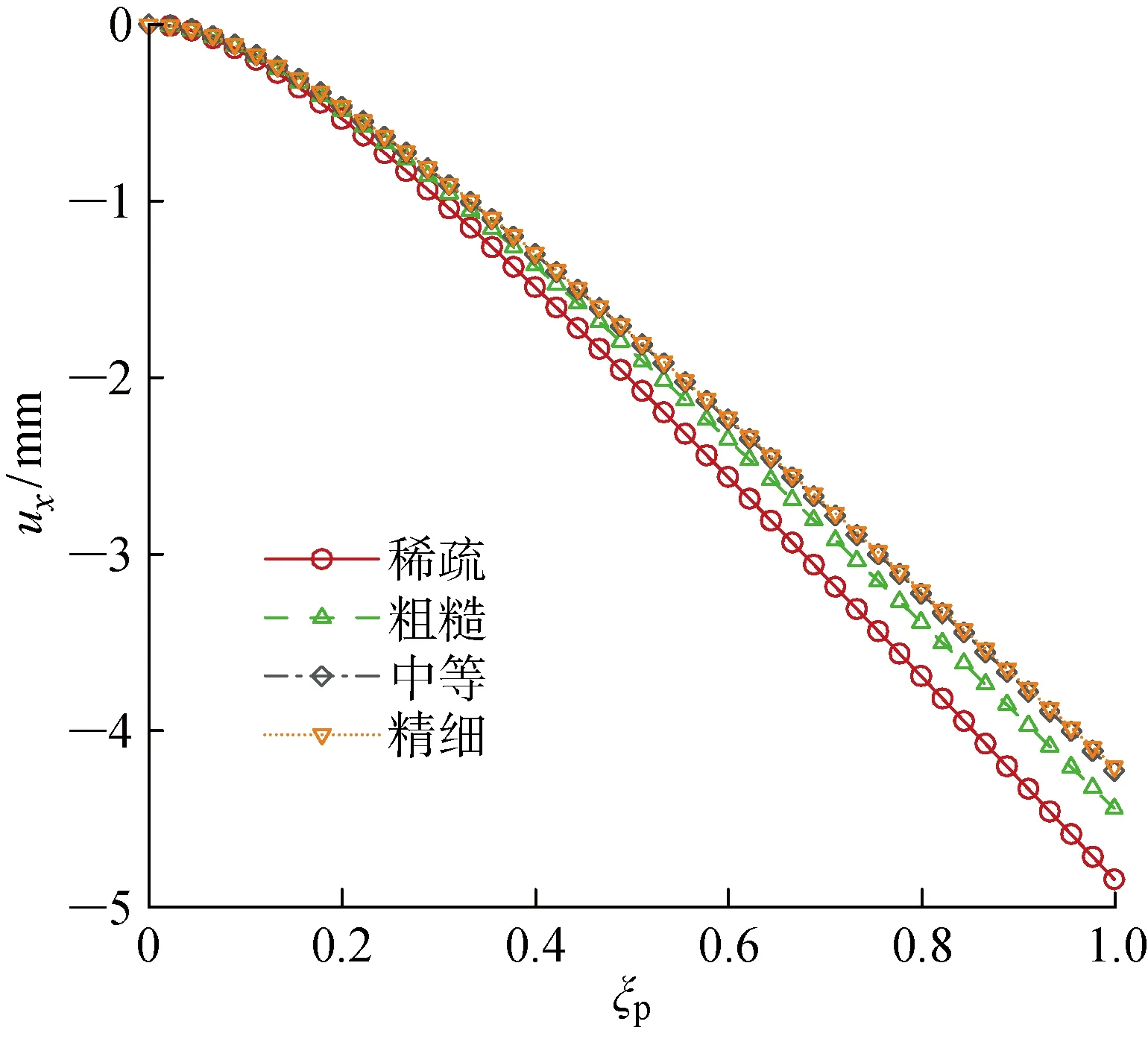
图10 Abaqus网格无关性分析Fig.10 Grid independence analysis in Abaqus

3 RPIM

RPIM结合了径向基函数的对称正定特点和无网格方法的优点，可以生成非奇异的插值矩阵，保证了数值稳定性，适用于任意分布的节点.而传统的径向基函数(RBF)，只能对气动压力分布进行较好的映射，而无法保证积分载荷(力与力矩)的守恒.而在RPIM中引入了线性基，可对积分载荷进行守恒插值，插值效果更接近真实情况.

3.1 位移传递矩阵

假设已知S个点的位移，待求点xh的位移u(xh)可由如下插值格式获得：

RT(xh)a+PT(xh)b

(9)

式中：ai为径向基函数Ri的未知权重系数；bj为多项式基函数Pj的未知系数；M为Pj中基底的个数；R为径向基函数矩阵；P为多项式基函数矩阵；a为权重系数向量；b为未知系数向量.

未知系数ai和bj通过求解类似于式(1)的方程获得，这里需要用到已知的S个点的位移，第t个点的位移ut为

(10)

t=1,2,…,S

将式(10)写成矩阵的形式为

u=Ra+Pb

(11)

式中：u为所有已知点的位移向量.

为保证方程封闭，需在式(10)的基础上施加如下约束：

(12)

j=1,2,…,M

为保证数据传递中力和力矩的平衡，要求多项式基函数至少取一阶，故M可取为4，则P(x)=[1xyz].联立式(10)和(12)可得：

(13)

或

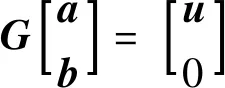
(14)

其中：

此处的RBF选取Wendland二阶光顺格式[19]

Ri(xk,yk,zk)=(1-ϑ)4(4ϑ+1)

(15)

式中：ϑ=li,k/rs，rs为径向基函数的支撑半径，li,k为点(xi,yi,zi)与点(xk,yk,zk)之间的距离.由于距离没有方向之分，所以矩阵R是对称正定的，则矩阵G也是对称的.

假设G可逆，则系数向量a为

a=R-1u-R-1Pb

(16)

再由式(13)可得：

b=S2u

(17)

(18)

将式(17)代入式(16)可得：

a=S1u

(19)

S1=R-1-R-1PS2

(20)

将式(17)～(20)代入式(9)可得待求点的位移为

u(xh)=[RT(xh)S1+PT(xh)S2]u

(21)

因此位移传递矩阵H可写为

式中：N为待求点个数.

3.2 节点力传递矩阵

为防止造成能量损失，可通过虚位移原理获得节点力传递矩阵.假设Ff和Fs分别为流体网格节点和固体网格节点上的力向量，uf和us为对应节点上的节点位移，由虚位移原理有：

(22)

已知位移传递矩阵H，即

uf=Hus

(23)

代入式(22)则有：

Fs=HTFf

(24)

3.3 CFD/CSD迭代过程

进行气动弹性计算时，需要在每个迭代步交换数据，该过程如图11所示.CFD模块将由计算获得的气动力数据①插值传递给CSD模块；然后CSD模块以①为输入载荷，通过计算过程②获得位移场数据③，并插值传递给CFD模块；CFD接收到位移后进行网格更新过程④，进而获得网格更新后的气动力数据⑤；通过插值将气动力数据⑤传递给CSD模块，如此完成一个迭代步的数据交换.随着迭代次数的增加，迭代结果会趋于收敛，此时可终止计算.

图11 CFD/CSD模块迭代过程Fig.11 Iteration process of CFD/CSD modules

3.4 RPIM插值精度及其效率对比

为说明使用RPIM进行流固耦合数据传递的必要性，分别使用RPIM和RBF对某Clark Y机翼表面进行气动力传递，径向基函数均如式(15)所示.NACA0014机翼插值精度验证如图12所示.由图12(a)可知，该机翼展向长度为10.5 m，机翼根部弦向长度为3.0 m，机翼后掠角为20.6°.该机翼的流场表面网格及固体网格如图12(b)和(c)所示.其中，机翼表面网格节点数为 3 140，固体网格表面节点数为 1 878.设定来流马赫数Ma=0.839 5，攻角α=3.06°，当地大气压为 100 312 Pa，当地温度为300.9 K.

图12 NACA0014机翼插值精度验证Fig.12 Interpolation accuracy verification for NACA0014 wing

对固体而言，表面载荷最终会转化为一致节点力，故此处直接选取网格节点力进行传递，避免再进行表面压力转换.表3统计了使用上述两种方式计算获得的各自传递矩阵并进行一次气动力传递后，在固体模型3个方向的合力(Fx、Fy、Fz)和力矩(Mx、My、Mz)大小.其中：er为相对误差；tc为计算耗时.由表3可知，在足够的精度范围内使用RPIM几乎没有能量损失，而由RBF获得的结果却与实际情况相差较远，最大相对误差为-348.8%.导致该结果的原因是RBF在数据传递过程中没有引入线性基，无法保证力与力矩的守恒，使用RBF传递节点力无法保证数据的有效性.从计算时间上来看，应用两种方式的总耗时分别为 20.03 s 和 32.13 s，RPIM的时间成本较RBF节省了约37.7%.对于相同的网格规模，虽然RPIM中的矩阵维度大于RBF，但由于RPIM只需求解一种传递矩阵(节点力传递矩阵或位移传递矩阵)，通过转置即可获得另一传递矩阵，而RBF需进行两次独立的矩阵求解，所以RBF在求解速度上较RPIM更慢.综上，所提RPIM插值方法能以较高的精度保证数据的准确性，在相同规模的网格前提下，能以更快的速度进行数据传递.

表3 CFD/CSD模块节点力传递结果Tab.3 Node force transfer results of CFD/CSD modules

4 螺旋桨气动弹性分析

设定螺旋桨飞行高度Hf=0 km，转速n=400～1 000 r/min，来流速度v=10 m/s，来流方向垂直于螺旋桨平面.当n=800 r/min时的气弹耦合过程如图13所示.其中：Is为计算迭代步数；ux,max为桨叶在x方向上的最大位移.由图13可知，当迭代到第5步时，结果业已收敛.故在后续分析中可约定最大迭代步数为5步，以第0步和第5步的流场计算结果作为变形前后气动弹性效应的对比依据.

图13 当n=800 r/min时的气弹耦合过程Fig.13 Aeroelastic coupling process at n=800 r/min

4.1 几何外形变化

当n=400～1 000 r/min时，桨叶尾缘在x和y方向的变形量变化情况如图14所示，其中uy为桨叶尾缘在y方向上的位移.由图14可知，当ξp<0.3时，位移量与径向位置呈现出近似二次关系；当超过该值后，位移量开始呈线性增加.说明桨毂的约束可以有效地拟制桨叶的变形能力，但作用范围只有桨叶径向30%的区域.桨叶在不同方向上的最大位移量与转速之间的关系如图15所示，其中umax为桨叶最大位移.由图15可知，当螺旋桨受到旋转气动载荷时，其主要变形不仅仅发生在来流方向，在旋转平面上依旧有相当可观的变形发生，uy,max平均可以达到ux,max的52.1%.当n=800 r/min时，ux,max为130.8 mm，达到了桨叶半径的5.7%.当n=1 000 r/min时，ux,max达到桨叶半径的9.4%，该量级的变形量说明螺旋桨在运行过程中产生的气弹效应不能被忽略.当n=1 000 r/min时，桨叶的扭转角Δε随桨叶径向位置的变化情况如图16所示.由图16可知，附加于螺旋桨表面的气动力会迫使桨叶的当地迎角增大，这将有利于推力的提高.

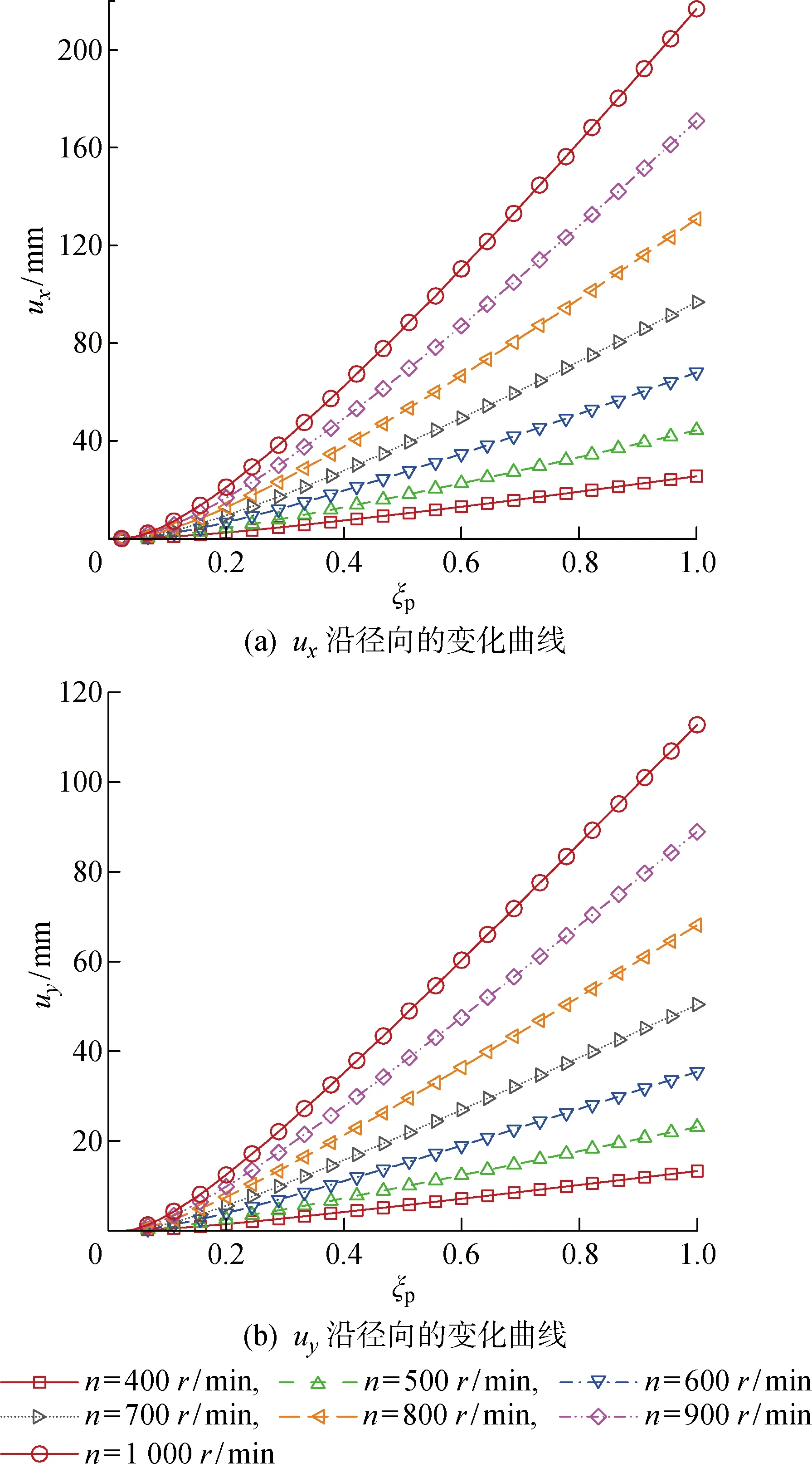
图14 桨叶尾缘的位移曲线Fig.14 Displacement curves of blade trailing edge

图15 x和y轴方向上的最大位移变化曲线Fig.15 Maximum displacements along x and y axes

图16 桨叶扭转角沿径向的变化Fig.16 Radial variations versus blade torsion angles

4.2 气动特性变化

螺旋桨变形前后的桨叶在背风面上的静压分布如图17所示，其中p为静压.由图17可知，在背风面上气动载荷几乎不因桨叶的变形而发生变化.螺旋桨变形前后的桨叶在迎风面上的静压分布如图18所示.由图18可知，其静压分布与图17有明显的差异.综合分析图17和18可知，在靠近桨毂的区域，刚性与柔性桨叶的静压分布几乎一致，说明变形未对该区域的流场造成影响；在远离桨毂的区域，即如红色虚线圈内所示，同一正静压在变形后的桨叶迎风面上占据更大的区域.这种静压分布结果会造成变形后的螺旋桨产生更大的推力和扭矩.结合图16与文献[20]中的翼型受力分析可知，造成柔性螺旋桨推力扭矩增大的原因在于桨叶的扭转变形增大了当地翼型的安装角，进而提高了当地迎角，使得迎风面正压区域扩大.

图17 螺旋桨背风面压力分布云图Fig.17 Distribution contour of propeller leeward pressure

图18 螺旋桨迎风面压力分布云图Fig.18 Distribution contour of propeller windward pressure

4.3 推进性能变化

前进比J，推力系数KF，扭矩系数KM和推进效率η的定义分别为

(25)

(26)

(27)

(28)

式中：ρ为空气密度.

变形前后推力系数随转速的变化曲线如图19所示，其中：Cr为刚性与柔性螺旋桨物理量的相对改变量.由图19可知，变形前后螺旋桨的推力变化趋势是一致的，增长速度由快变慢，但变形后的螺旋桨较刚性螺旋桨能够产生更大的推力，且差距随着转速的增加而增加，最大改变量达到7.2%.扭矩系数的变化情况如图20所示.由图20可知，当不考虑螺旋桨变形时，扭矩系数先增加继而保持相对的稳定；而对于柔性螺旋桨而言，当n>500 r/min后，扭矩系数基本上保持线性增加，最大改变量可达9.9%.螺旋桨推进效率的变化情况如图21所示.由图21可知，随着负载的增加，刚性和柔性螺旋桨的效率逐渐降低，柔性螺旋桨效率略低于刚性螺旋桨，两者的变化趋势整体上保持一致，最大改变量仅为-2.4%，可认为气动弹性在本文工况下基本不会影响螺旋桨的推进效率.

图19 气动弹性对推力系数的影响曲线Fig.19 Influence of static aeroelasticity on thrust coefficient

图20 气动弹性对扭矩系数的影响曲线Fig.20 Influence of static aeroelasticity on torque coefficient

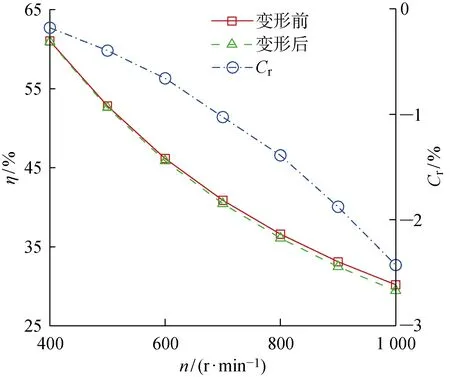
图21 气动弹性对效率的影响曲线Fig.21 Influence of static aeroelasticity on efficiency

5 结论

(1) 当螺旋桨运转时，在旋转平面上的变形约为来流方向上的52.1%，当转速升至 1 000 r/min时，沿来流方向的最大变形量为桨叶半径的9.4%，气动弹性效应不能被忽略.

(2) 螺旋桨背风面上压力分布几乎不因桨叶的变形而发生变化，远离桨毂时，桨叶的变形增大了当地翼型的迎角，使得同一正压在变形后的桨叶迎风面上占据更大的区域.

(3) 相较于刚性螺旋桨，柔性螺旋桨能够产生更大的推力，且差距随转速的增加而增加，最大改变量达7.2%.当转速高于500 r/min后，扭矩系数基本保持线性增加，最大改变量达9.9%.随着转速的增加，柔性和刚性螺旋桨的效率略有降低，最大改变量为-2.4%，可认为柔性螺旋桨的推进效率基本不受气动弹性的影响.

(4) 本文形成的柔性螺旋桨气动弹性分析框架，对各类铺层结构的螺旋桨均适用，实际应用中针对具体情况修改材料的力学属性即可.