基于机器视觉和盲源分离的机械故障检测

彭 聪，刘 彬，周 乾

(南京航空航天大学 自动化学院，南京 210016)

机械的运行状态直接关系到设备的生产状态，对其进行故障诊断及状态监测是非常必要的.振动信号是反映机械的运行状态的重要指标，通过对振动信号的分析与处理可以实现故障诊断与状态监测.对振动信号的测量通常采用传统测量仪器，如加速度传感器，一些基于传统方式测量的故障诊断与检测方法能够取得较为准确的结果[1-4].然而，当被测物体相对较小时，采用加速度传感器容易造成质量负载效应；当被测物体相对较大时，采用加速度传感器进行信号采集，难度大、成本高以及耗时耗力[5].因此，采用传统接触式测量方法具有很大的局限性.近年来，基于视觉的振动测量技术吸引了很多研究者的兴趣，许多研究人员提出了基于视觉测量的机械故障诊断方法[6-9].与传统测量方式相比，基于机器视觉的测量方法可以进行非接触式测量，适用于高温高压等危险场合，能够实现全场振动测量等优点[10].

机械设备在运行过程中，不仅产生振动，还发出强烈的噪声，因此，振动信号经常混有其他振源及噪声等干扰成分，影响信号的分析与处理.盲源分离作为一种信号分析和数据处理技术，无需源信号的特征及混合条件就能够从观测到的混合信号中通过逆变换分离出源信号.盲源分离的实质是从未知信号的混合观测信号中重构出原始的源信号[11].根据混合通道数，可分为单通道和多通道信号盲源分离；根据源信号混合信号的组合特性，可分为线性和非线性盲源分离[12-13].盲源分离在很多领域中得到了广泛的应用：文献[14-18]提出了基于盲源分离的信号分离算法对混合信号进行分析与处理；文献[19-21]提出基于盲源分离的识别算法进行桥梁结构的模态阻尼估计和刚性结构的运动分析；文献[22]提出采用盲源分离用于处理生物医学信号.近年来，盲源分离得到快速发展，并被广泛应用于机械的多源故障诊断中[23-25].这些基于盲源分离的机械故障诊断方法虽然能够实现较为准确的诊断结果，但这些方法大都采用传感器阵列获取观测信号，当设备的系统结构较为复杂，环境比较恶劣时，采用传感器进行接触式信号采集具有很大的局限性，并不能很好地进行推广应用.

为有效解决机械转子的多源故障情况，本文结合机器视觉测量方法和盲源分离信号处理方法，提出了基于机器视觉和盲源分离的旋转机械故障检测.用机器视觉的方法获取高速视频并采用盲源分离方法对获取的高速视频进行分析与处理.最后，实验证明该方法能够对旋转机械的多源故障进行准确定位并进行有效的分离识别.

1 基于机器视觉的盲源分离数学理论

基于机器视觉和盲源分离的故障检测数学理论的流程如图1所示：首先输入图像序列进行金字塔分解，然后基于相位进行振动位移提取,最后采用快速独立成分分析算法(Fast-ICA)得到分离后的信号.

图1 高速视觉和相位运动分析的盲源分离示意图Fig.1 Schematic diagram of blind source separation for high-speed vision and phase motion analysis

1.1 盲源分离信号模型

盲源分离信号模型采用线性混合模型，线性混合模型适用于结构力学刚度大以及信号混合延时小的对象，可靠性高，是旋转机械故障检测中常用的数学模型.假设存在n个振动源Si(t),i=1,2,…,n，统计独立，此n个信号经过线性混合后得到m个观测信号.每个观测信号为n个源信号的线性组合.线性混合后的观测信号可表示为

(1)

式中：aij为线性混合参数，i∈{1,2,…,m},j∈{1,2,…,n}；xi(t)为混合后的观测信号；sj(t)为源信号；ni(t)为干扰噪声.将式(1)变化成矢量形式可得在t时刻的观测信号：

x(t)=As(t)+n(t)

(2)

1.2 基于机器视觉的盲源信号分离方法研究

为了弥补基于传统接触式振动测量的盲源分离方法存在的不足，本节提出了基于高速视觉的盲源分离方法，实现了从振动视频中恢复出振源信息.假设采集到的视频序列为

It={I(x,y,t0),I(x,y,t1),I(x,y,t2),…,

I(x,y,tn)}

(3)

将当ti时刻的图像I(x,y,ti)经过复系数可控金字塔进行空间分解，得:

Ai(γ,θ,x,y,ti)eiφi(γ,θ,x,y,ti)=

I(x,y,ti)(Gθ+iHθ)

(4)

式中：Ai为幅值；φi为相位；i表示虚部单位；Gθ+iHθ为Gabor滤波器的复数形式；Gθ和Hθ可表示为

(5)

式中：x,y为空间位置；λ为正弦波的波长；θ为Gabor滤波器核中平行条纹的方向；ψ为相位偏移；σ为高斯函数的标准偏差；γ为空间长度比.根据式(4)可计算参考帧的相位为φ0，相位差为

Δφi=φi-φ0

(6)

得到相位差矩阵AΔφ(H×V)|θ=θ0，H×V为图像分辨率，θ0为参考帧的方向.结合具体测量要求和振动强度分布可得观测向量的具体像素坐标为{(x1,y1),(x2,y2),…,(xj,yj)}.计算图像序列中每一帧在此坐标处的相位差，相位差和位移成线性关系.因此可以得到观测信号向量:

D=[d1d2…dj]

(7)

式中：di=[Δφ1Δφ2… Δφn].对D进行白化，降低信号相关性，白化过程可以表示为

Z(t)=QD

(8)

式中：Q为白化矩阵；Z(t)为白化后的信号.采用Fast-ICA迭代算法，对Z(t)进行分离.

1.3 超定视觉盲源分离

当前分析盲源分离问题时都假定观测信号和源信号数量一致，但在实际应用中，观测信号往往会大于或小于源信号，甚至源信号数量会产生动态变化，造成超定或欠定.在视觉盲源分离方法中，由于图像可以在全场景下提供任意位置的振动信息，所以能够避免欠定问题.超定情况下，观测信号数量大于源信号数量，一般算法难以解决超定情况下的问题.分集合并技术可以有效减少观测信号之间的相关性，并且可以提高输出信号的信噪比.本文将分集合并技术与视觉盲源分离方法进行结合，提出融合分集合并技术的视觉超定盲源分离方法，对观测信号先进行分集解算再进行合并，从而将超定问题转换为适定问题.

融合分集合并技术的视觉超定盲源分离算法具体流程如下：

步骤1输入视频序列I(x,y,t)，选择感兴趣区域，对图像进行空间分解和时域滤波，得到局部运动位移向量d=[d1d2…dm].

步骤2对位移向量进行分集处理，在位移向量d=[d1d2…dm]中随机选择n个组成n维观测向量d=[d1d2…dn].

步骤3将步骤(1)和(2)执行k次，得到k个n维观测向量di,i=1,2,…,k.

步骤5利用信号的相关性对得到的源估计信号进行分类，得到n个分类后的信号yl=[y1ly2l…ykl]T，l=1,2,…,d.

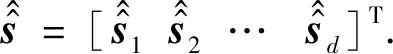
2 实验部分

图2所示为双转子实验平台，主要由直流无刷电机、调速器、轴承座、底座、柔性双跨转子、联轴器、加速度传感器、高速工业相机、光源、数据采集卡和两个振源构成.当该实验平台在高速实验中时，分别对两套转子系统施加2 g的质量不平衡，并分别设置电机转速为 1 800 r/min和 2 700 r/min.设置图像分辨率为 1 000像素×45像素；相机帧率为100 帧/s；采集时长为3 s.待电机转速稳定以后，进行数据采集.

图2 基于机器视觉的多源故障分离实验场景Fig.2 Experimental scene of multi-source fault separation based on machine vision

通过基于机器视觉的振动测量得到六路混合后观测信号的时域波形如图3所示(Δφ为相位差，t为采样时间).

图3 基于视觉采集到的观测信号时域波形图Fig.3 Time-domain waveform diagram of observation signals collected based on vision

为验证融合分集合并技术的视觉超定盲源分离的有效性，将其与普通适定方法结果进行对比.选择时域信号a1和b2，未采用分集合并技术时分离后的结果如图4所示(A为相位幅值，f为频率).对比图4(b)和4(d)，在频域内有30 Hz和45 Hz两个主要频率，幅值谱相似，阶次均为×1和×1.5，符合基础松动故障特征，但无法通过频谱图判断振源信息.

图4 未分集情况下视觉盲源分离的时频域波形Fig.4 Time-frequency domain waveform of blind source separation without diversity

未分集分离后，混合系统的全局矩阵(GA)和性能指数(PI)如表1所示，此时不能对混合信号进行有效分离.对输入观测信号采用二重分集处理和四重分集处理并增加输入信号，二重分集时选择的观测点为a1、a2和b2，分集后输入信号为s1=[a1a2]；s2=[a1b2].对输入观测信号进行二重分集处理后的盲源分离结果如图5所示.

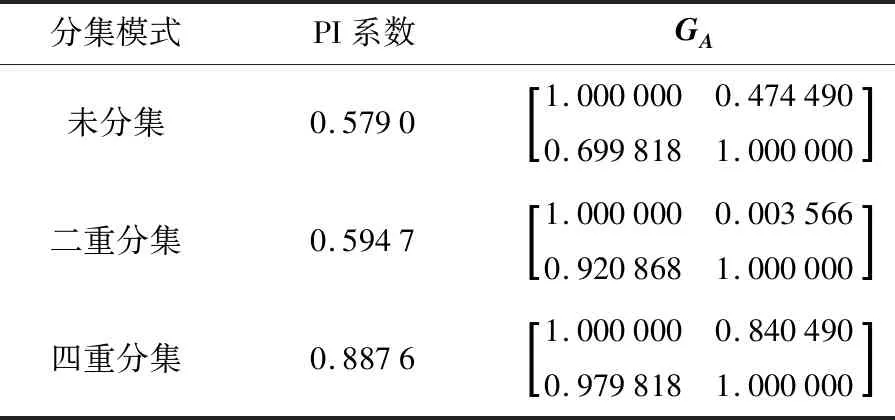
表1 不同分集模式下PI系数与全局矩阵表Tab.1 PI coefficients and global matrix table in different diversity modes

观察图5频谱图可知，分离信号各自的频谱含有×1.5、×2和×3频率分量，虽然幅值相应减少但仍没得到较好分离.对输入信号进行四重分集处理，选择观测点为a1、a2、b1和b2，分集后的输入向量分别为s1=[a1a2]；s2=[a1b1]；s3=[b1b2]和s4=[a2b2].

图5 二重分集时的视觉盲源分离结果Fig.5 Results of visual blind source separation in double diversity

四重分集处理的结果如图6所示，分离信号的频谱中不含有×1.5频率分量，频谱峰值分别为 30 Hz 和45 Hz，此时能够准确估计源振动信号的信息.

图6 四重分集时的视觉盲源分离结果Fig.6 Results of visual blind source separation in quadruple diversity

为进一步探究分集合并参数对系统的影响，改变不同分集数和观测信号的数量进行探究.图7为分集数以及观测信号数对信噪比(SNR)的影响，从图7(a)可得随着分集数的增加，分离出的估计信号的信噪比逐步提高.从图7(b)可得随着观测信号的增多，分离出估计信号的信噪比也随之提高.可见分集数量的增加以及观测信号数量的增加均可提高输出信号的信噪比.单纯增加观测信号数量虽然能获取更多源信号的信息，但提高了输入信号之间的相关性,通过增加分集数量可有效降低信号的线性相关性.

图7 参数变化对SNR的影响Fig.7 Effects of parameter variations on SNR

图9 分离后的加速度估计信号Fig.9 Acceleration estimation signal after separation

为验证超定视觉盲源分离方法的有效性，将上述实验结果与两通道加速度传感器的分离结果进行对比，图8和9所示分别为加速度传感器得到的观测信号和分离后的信号(a为加速度).从分离结果可见分离信号各自的频谱上仍有×1和×1.5频率分量，由此说明并没有较好分离出两个不平衡振动信号.综合上述实验结果可知，传统接触式盲源信号分离在受到传感器数量、位置和方向限制时，难以对混合信号进行准确解算.而本文提出的视觉盲源分离方法及其在超定情况下的应用能够有效解决此类问题.

本实验通过基于机器视觉的测量得到若干混合后的观测信号,对观测信号未进行分集处理时，无法通过频谱图判断振源信息，源信号不能得到较好分离.对输入观测信号采用分集处理，首先进行二重分集处理，采用二重分集处理只是使幅值得到相应减少并没有实现较好的分离.然后对输入信号进行四重分集处理，经过四重分集处理后，可以看出频谱图中不含有×1.5、×2和×3频率分量，输入信号得到分离，采用四重分集处理能够准确识别振源信息.为了探究分集合并参数对系统的影响，对不同分集数和观测信号的数量进行实验.结果表明，随着观测信号的增多和分集数量的增加，估计信号的信噪比也随之增加.只增加观测信号数量,虽然能获取更多源信号的信息，但会提高输入信号之间的相关性,增加分集数量可以有效降低信号的线性相关性.最后，为了进一步验证融合分集合并技术的视觉超定盲源分离的有效性，将融合分集合并技术的视觉超定盲源分离结果与基于加速度传感器的分离结果进行对比.结果表明基于传统接触式的盲源信号分离在受到传感器数量、位置和方向限制时，难以准确对混合信号进行解算，从而验证了超定视觉盲源分离的有效性.

3 结语

本文提出了一种基于机器视觉和盲源信号分离的旋转机械多源故障检测方法.该方法对高速视频进行分析，可获得全视角内多方向的振动信息，以解决传统基于盲源信号分离的多源故障检测中存在的振动信号位置不确定的问题.在此基础上，采用盲源信号分离方法和超定视觉盲源分离方法对获取的高速视频进行分析.最后，对所提出的方法进行实验研究，并与传统基于加速度传感器的分离结果进行对比，实验结果表明，本文中所提出的多源故障检测方法可准确定位故障区域，对多源故障进行有效分离及识别.