关注同构特点 启迪函数解题

崔常娥

(江苏省射阳县教师发展中心 224300)

函数作为高中数学重要的组成模块，因其具有广泛的融合性和较强的针对性，所以通过对融合不同知识点的例题综合考察，培养学生综合运用知识和多方面的能力.简而言之，掌握函数知识解决函数问题，尤其是能够对不同类型函数问题进行归纳整理，形成自己的解题思路是十分重要的.下面将结合实例探讨如何利用同构特点解决函数结构式完全相同变量却不同的函数问题.

一、观察函数结构，利用同构求参数值

三角函数有关知识点比较简单，但因为其特殊的结构往往能够让学生对解决表达式复杂的三角函数问题感到吃力.当三角函数与不等式、高次结合在一起时，学生更易被此类问题的虎威所吓蒙，不知如何入手.针对此类问题，需要学生保持平常心，就事论事，如：

例1若关于θ的不等式满足cos5θ-sin5θ<7(sin3θ-cos3θ)，θ∈[0,2π)，则θ的最小取值是____.

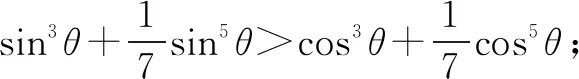
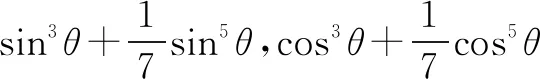
二、对比已知条件，深挖同构解参数范围

若利用已知条件可以得到f(a)=0，f(b)=0两个方程具有同构的特点，则可以将a,b看作是方程f(x)的两个根，如：

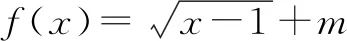
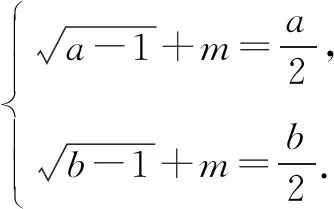
三、挖掘隐含信息，依据同构解函数值

函数单调性、奇偶性、周期性等有关函数性质的内容，常常是解题的切入点，因此，看到题目中含所有函数性质的字眼要多加留神.看到函数单调性，要自动联想到函数图象的走向、函数的取值趋势等内容；看到函数的奇偶性，头脑中要主动出现奇偶函数的定义域特点、奇偶函数的性质等，借助关键字眼，快速延伸有关信息，是解决问题的关键，如：

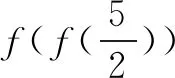
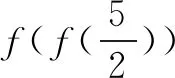
总之，借助同构性解决除变量以外结构式完全相同的函数问题，关键在于能够发现与问题的内在某种关系，深入剖析，积极展开正确丰富的联想，借助性质进行一系列的转化，最终使得问题化难为易、化繁为简.