高考考查递推公式的常见类型与解法

廖永福 林永志

(1.福建省厦门第二中学 361009；2.福建省仙游于洁小学 351256)

递推公式是表示数列的一种方法，它揭示了相邻几项之间的关系，而项与项数之间的关系比较隐蔽，因此蒙上了一层神秘的面纱，给教学带来一定的困难.解决这类问题的关键是选择适当的方法去求数列的通项公式，常用的方法有：定义法、公式法、累加法、累乘法、构造法和归纳法等.现分述如下：

一、定义法

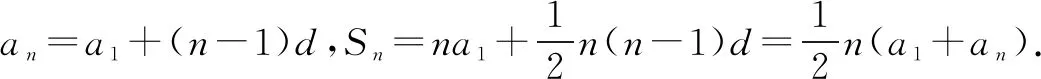
例1 (2020·全国卷Ⅱ) 数列{an}中，a1=2，am+n=aman，若ak+1+ak+2+…+ak+10=215-25，则k=( ).

A．2 B.3 C.4 D.5

分析令m=1，可得数列{an}是等比数列，求出数列{an}的通项公式，利用等比数列求和公式可列出关于k的方程，由k∈N*可求得k的值.

解答在等式am+n=aman中，令m=1，可得an+1=ana1=2an.

又a1=2，所以数列{an}是首项为2，公比为2的等比数列，an=2×2n-1=2n.

∴2k+1=25，则k+1=5，解得k=4.故选C.

点评本题考查递推公式和等比数列的求和公式，考查计算能力和方程思想.关键是由递推公式得出an+1=2an，进而得出数列{an}是等比数列，属于中等题.

二、公式法

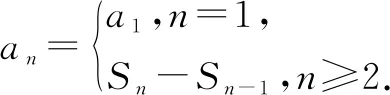
例2 (2020·江苏卷))设{an}是公差为d的等差数列，{bn}是公比为q的等比数列，已知数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*)，则d+q的值是____.

分析由数列{an+bn}的前n项和Sn求出an+bn，再结合数列{an}是公差为d的等差数列，{bn}是公比为q的等比数列，求出d和q，进而求出d+q的值.

解答数列{an+bn}的前n项和Sn=n2-n+2n-1(n∈N*)，

当n≥2时，an+bn=Sn-Sn-1=2n-2+2n-1.

∵a1+b1=S1=1适合上式，∴an+bn=2n-2+2n-1(n∈N*).

又∵{an}是公差为d的等差数列，{bn}是公比为q的等比数列，

∴an=2n-2，bn=2n-1，

∴d=q=2，故d+q=2+2=4.

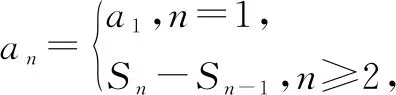
例3 (2012·全国卷大纲版)已知数列{an}的前n项和为Sn，a1=1，Sn=2an+1，则当n>1时，Sn=( ).

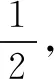
解法一由Sn=2an+1，得Sn-1=2an(n≥2).

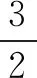
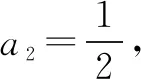
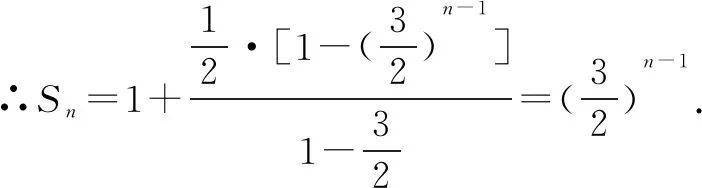
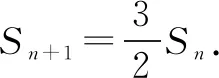
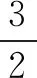
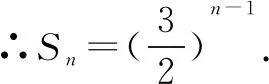
点评本题考查递推公式与等比数列的通项公式、前n项和公式，考查推理能力与计算能力.消去an，还是消去Sn，要视具体情况而定，一般以简便为原则，属于中档题．

三、累加法

形如an+1-an=f(n)的递推公式，可用累加法求出an，即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)，进而解决问题.

例4 (2014·全国卷大纲版)数列{an}满足a1=1，a2=2，an+2=2an+1-an+2．

(1)设bn=an+1-an，证明{bn}是等差数列；

(2)求{an}的通项公式．

分析(1)将an+2=2an+1-an+2变形为an+2-an+1=an+1-an+2，即bn+1=bn+2，根据等差数列的定义可以判定；(2)由(1)及等差数列的通项公式求出bn，代入bn=an+1-an，再用累加法求出{an}的通项公式．

解答(1)由an+2=2an+1-an+2得，an+2-an+1=an+1-an+2.

∵bn=an+1-an，∴bn+1=bn+2，即bn+1-bn=2.

又∵b1=a2-a1=1，∴{bn}是首项为1，公差为2的等差数列．

(2)由(1)得bn=1+2(n-1)=2n-1，即an+1-an=2n-1，又a1=1，

∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+1+3+5+…+2(n-1)-1

∴{an}的通项公式为an=n2-2n+2．

点评本题考查等差数列的定义、通项公式、前n项和公式，以及用累加法求数列的通项公式的方法，考查了转化思想，属于中档题．

四、累乘法

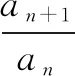
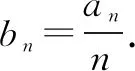
(1)求b1，b2，b3；

(2)判断数列{bn}是否为等比数列，并说明理由；

(3)求{an}的通项公式．

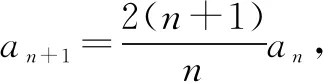
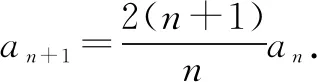
(2)数列{bn}是首项为1，公比为2的等比数列.

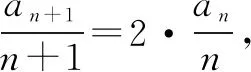
点评本题考查数列的递推公式、等比数列的定义和通项公式．事实上，本题若用累乘法求解，则别有一番滋味，解答如下：

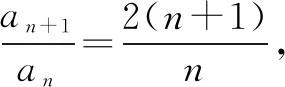
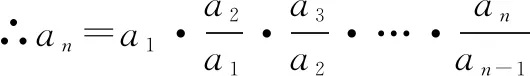
=n·2n-1.

∴an=n·2n-1，故bn=2n-1.至此，(1)(2)便迎刃而解.

五、构造法

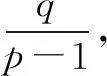
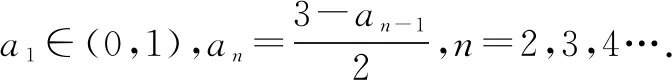
(1)求{an}的通项公式；

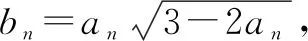
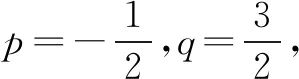
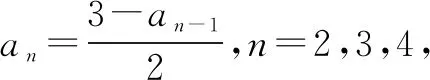
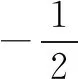
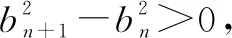
点评本题考查数列的递推公式，等比数列的通项公式和不等式的证明等，解题时要认真审题，注意挖掘题设中的隐含条件．用“同加法”构造出等比数列是解题的关键，属中档题.

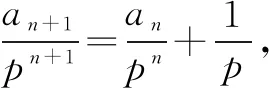
例7 (2009·全国卷Ⅱ)设数列{an}的前n项和为Sn，已知a1=1，Sn+1=4an+2(n∈N*)．

(1)设bn=an+1-2an，证明数列{bn}是等比数列；

(2)求数列{an}的通项公式．

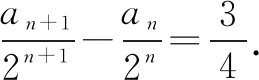
解答(1)由a1=1，及Sn+1=4an+2，得a1+a2=4a1+2，a2=3a1+2=5，所以b1=a2-2a1=3．

由Sn+1=4an+2，则当n≥2时，有Sn=4an-1+2，两式相减，得an+1=4an-4an-1，所以an+1-2an=2(an-2an-1)(n≥2).

∵bn=an+1-2an，∴bn=2bn-1(n≥2)，∴{bn}是首项为3，公比为2的等比数列．

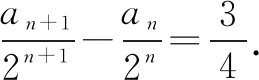
点评本题考查了等差数列和等比数列的通项公式，考查了定义法、公式法和构造法，考查转化和化归思想和综合运用知识的能力．属中难题.

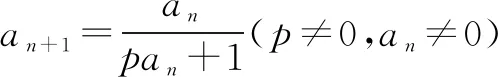
想一想：形如panan+1=an-an+1(p≠0,an≠0)的递推公式，该怎样变形？

例8 (2015·全国卷Ⅱ)设数列{an}的前n项和为Sn，且a1=-1，an+1=Sn+1Sn，则Sn=____．

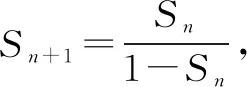
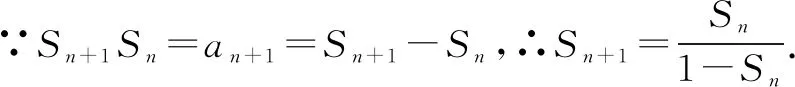
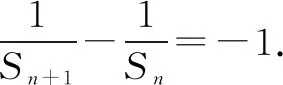
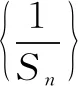
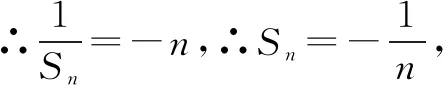
点评本题考查数列的递推公式，等差数列的通项公式等，用同取倒数法构造出等差数列是解决本题的关键，属于中档题．

六、归纳法

若题目所给的递推公式不属于上述情形，则可根据递推公式计算出数列的一些项，观察其特征、找出相应的规律，归纳出一般性的结论并加以证明，进而解决问题.

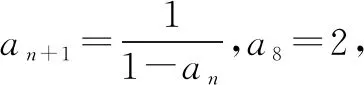
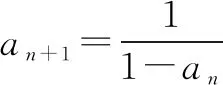
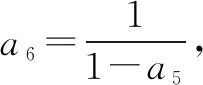
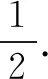
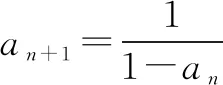
∴数列{an}是周期为3的周期数列.

点评本题考查数列的递推公式和周期数列的性质，关键在于从计算出数列的一些项中找出规律，归纳出一般性结论，属于基础题．

例10 (2020·全国卷Ⅲ)设数列{an}满足a1=3，an+1=3an-4n.

(1)计算a2，a3，猜想{an}的通项公式并加以证明；

(2)求数列{2nan}的前n项和Sn.

分析(1)利用递推公式计算a2,a3，猜想得出{an}的通项公式，再用数学归纳法证明；(2)用错位相减法求解.

解答(1)由题意可得a2=3a1-4=9-4=5，a3=3a2-8=15-8=7.

由数列{an}的前三项可猜想数列{an}是以3为首项，2为公差的等差数列，即an=2n+1.

证明如下：当n=1时，左端=a1=3，右端=2×1+1=3,成立.

假设当n=k时，ak=2k+1成立,那么

当n=k+1时，ak+1=3ak-4k=3(2k+1)-4k=2k+3=2(k+1)+1也成立.

故对任意的n∈N*，都有an=2n+1成立.

(2)由(1)可知，an·2n=(2n+1)·2n.

Sn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n①,

2Sn=3×22+5×23+7×24+…+(2n-1)·2n+(2n+1)·2n+1②.

由①-②，得-Sn=6+2×(22+23+…+2n)-(2n+1)·2n+1

∴Sn=(2n-1)·2n+1+2.

点评本题主要考查求等差数列的通项公式以及利用错位相减法求数列的和，属于中档题.

递推关系问题的考查形式灵活多样，同时隐含着丰富的数学思想，解题时不仅要认真审题，抓住递推公式的特点，选择适当的方法，而且还要注重用函数与方程、转化与化归等数学思想方法指导解题实践，把提升数学素养真正落到实处.