过测地线网的组合双三次Bézier曲面优化设计

杨火根，毛小红

(江西理工大学理学院，江西省 赣州市 341000)

1 引言与研究背景

测地线是曲面上测地曲率处处为零的曲线[1]。测地线有着优美的几何性质，在各行各业有着广泛的应用。如生物医学图像处理[2-4]、膜结构裁剪分析[5-6]等。

近些年，曲面造型领域涌现出了一大批关于过测地线的曲面设计研究成果。Wang[7]提出一种以一条曲线为公共测地线的曲面参数化设计方法，以此实现曲面重建，并应用于鞋帽和服装制造业。文献[8]提出了以一条非均匀B样条曲线为公共测地线来构造NURBS曲面束。Sánchez[9]采用两步法，给出了设计Bézier曲面插值非相交等参曲线(组)为边界测地线的算法。此外还研究了过测地线的极小曲面设计问题，并指出插值测地圆和螺旋线为测地线的极小曲面就是悬链面和Scherk曲面[10]。Paluszny[11]则利用测地线的几何性质，并结合直纹面和可展曲面的特点，给出了过测地线的插值曲面构造的一般结果。Sprynski等人[12]以两条等参测地曲线为曲面边界线，利用Hermite插值完成曲面重建。寿华好等人[13-14]则提出了一种以B样条为度量函数的过一条或多条测地线的离散曲面构造算法。对于相交曲线，Farouki等人[15]研究了四边形曲线为某曲面上测地线的约束条件。在此基础上，基于Coons超限超值方法分别给出了张量积Bézier曲面、三角B-B曲面插值四边形和三边形曲线为曲面边界测地线的优化设计方法[16-17]。然而基于Coons方法构造的曲面存在次数过高、自由参数对曲面形状的影响具有整体性、曲面形状不易控制等缺点。为此，Yang等人[18-19]基于分步构造策略，给出了较低次数的Bézier和B样条曲面插值测地四边形的曲面优化设计方法。对拓扑结构更为复杂的网状测地线情形，Yang等人[20]给出了存在曲面以多条交于一点的曲线为曲面上测地线网的一般约束条件。但对过测地线网的插值曲面构造，特别是多项式曲面的构造研究还较少见。因此，本文基于交于一点的曲线网为曲面上测地线网的一般约束条件，以工程中常用的Bézier曲线为工具，考虑过交于一点的三次Bézier测地线网的Bézier曲面重构问题。

2 三次Bézier曲线网为曲面上测地线网的约束

2.1 预备知识

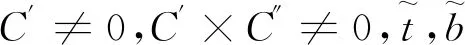
(1)

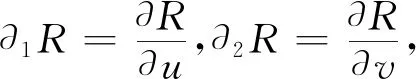
设Ci：[0，1]→R3，i∈Zn={1，2，…n}是n条空间曲线序列构成的曲线网，记

(2)

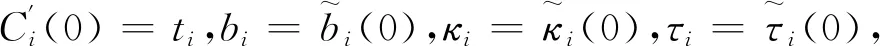
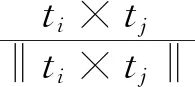
对曲线网Ci定义三类约束如下:

·副法矢约束:

bi·n=0

(3)

·相交测地线约束:

(4)

·顶点围绕约束:

(5)

文献[20]给出了存在曲面插值该曲线网Ci为曲面上测地线网的一般性约束条件，即:

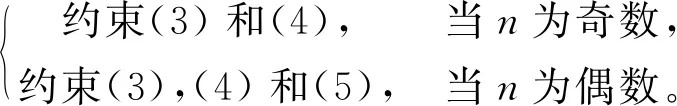
由引理1易知，当n为偶数且：

(ⅰ) 所有曲率κi相等时，顶点围绕约束(5)自然满足，相交测地线约束(4)简化为:τi+τj=0。即相邻曲线的挠率不互为相反数时，插值曲面是不存在的。

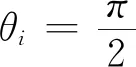
2.2 过三次Bézier测地线网插值曲面存在性条件

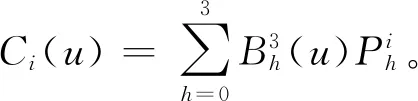
(1) 副法矢约束

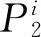
(6)

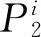
(2) 相交测地线约束

令

(7)

其中，

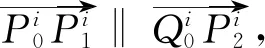
所以

即

(8)

又

(9)

(3) 顶点围绕约束

(10)

即当n为偶数时，给定的角点信息需满足整体约束(10)。

3 过测地线网的组合双三次Bézier插值曲面优化设计

在曲线网Ci满足引理1条件下，本节考虑插值该曲线网为测地线网的组合双三次Bézier曲面优化设计方法，给出曲面控制顶点的显式计算步骤，记这n张双三次Bézier曲面为:

(11)

3.1 公共边界控制顶点

如图1所示，因曲面Ri(u，v)插值n条曲线网Ci为公共边界曲线，所以有:

(12)

由式(12)及Bernstein基的线性无关性，可得曲面Ri(u，v)的公共边界控制顶点为:

(13)

3.2 邻接公共边界控制顶点

由测地线的几何性质可知，插值曲面沿测地线Ci(t)的跨界切矢可表示为:

(14)

其中，

根据跨界切矢计算插值曲面邻接边界线的控制顶点时，交点P0附近会产生切矢和扭矢相容问题。

(1)切矢相容

解得

(15)

(2) 扭矢相容

(16)

(17)

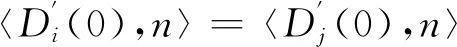
(18)

其中，

(19)

其中，

根据式(14)和(19)，跨界切矢Di(t)可用如下三次Bézier曲线表达:

(20)

其中

(21)

3.3 组合曲面自由控制顶点

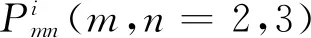
(22)

(23)

其中，

3.4 插值曲面优化设计算法步骤

基于以上分析，构造组合双三次Bézier曲面插值曲线网Ci(i=1，2，…，n)为曲面边界测地线网的步骤与如下:

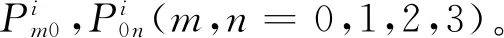
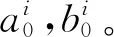
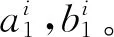
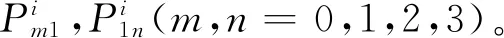
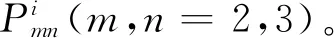
4 计算实例与比较

利用3.4节的算法，本节给出插值不同条数测地线网的曲面构造实例，并与传统的Coons方法[15-16]作比较。由于本文曲面仅插值两条相邻边及跨界切矢，Coons曲面构造格式如下:

Ri(u，v)=R1(u，v)+R2(u，v)-R0(u，v)

(24)

其中，

Hi(t) (i=0，1，2，3)为三次Hermite基。

显然曲面(24)中跨界切矢Di(t)的自由参数一旦确定，曲面将唯一确定，即自由参数对曲面形状影响具有全局性。对比本文提出的优化设计算法，Di(t)的自由参数仅影响邻接公共边界的控制顶点，即自由参数对曲面的影响是局部的，曲面的形状还受其他控制顶点的影响。

图2，3，4分别给出了测地线网中曲线条数n=4，5，6的计算实例。(图中渐变色条的数值表示曲面高度)

5 结论

本文分析了存在曲面插值三次Bézier曲线网为曲面的边界测地线网的三类约束条件，该约束本质上是对曲线网控制顶点的约束。并提出了一种构造组合双三次Bézier曲面插值该曲线网为曲面上测地线网的优化设计算法。与传统的Coons方法相比，本文采用分步和优化计算控制顶点的策略，使自由参数对曲面形状的影响具有局部性，曲面形状易控制且具有整体最优性。同时插值曲面表示为标准的张量积Bézier形式，与CAD系统兼容，方便交互操作。该算法可扩展到过任意拓扑类型测地线网的插值曲面构造中去。