±1100kV特高压输电塔风振响应频域分析

(同济大学土木工程学院，上海，200092)

特高压直流输电线路具有低投资、低电损和节约土地等优点，特别适合于远距离、大容量的电力输送[1]。±1 100 kV 特高压输电线路承担的电压等级高、电气间隙要求大，导致输电塔结构横担较长。长横担结构导致输电塔结构转动惯量大，1 阶扭转频率低。其1 阶扭转频率常与1 阶弯曲频率接近[2]，甚至低于1 阶弯曲频率[3-4]。我国相关标准[5-6]提出的顺风向风荷载计算公式仅适用于以第1阶振型(一般为弯曲平动)起绝对主导作用的悬臂结构。因此，对于结构前几阶频率趋于接近的长横担输电塔，规范方法的适用性值得研究[6]。针对长横担输电塔结构风振响应的研究已逐渐展开[2-3,7-9]。聂建波等[2]对±800 kV 特高压输电塔进行有限元动力时程分析，建议横担部分的风振系数为同等高度塔身节段风振系数的1.3 倍；张骞等[3]研究了±1 100 kV 输电塔线体系风振响应，认为横担长度及风向角是影响塔身扭转效应的重要因素；楼文娟等[9]对角钢塔进行风洞试验研究，发现横担端部测点的加速度为塔身相同高度的1.56～2.45 倍。上述研究得到较为一致的结论，即风致振动中长横担输电塔的扭转效应不可忽略。这些研究分别采用动力时程分析和风洞试验的方法，其中，时程分析需要耗费大量计算时间且无法考虑振型对结构响应的贡献；风洞试验无法按几何缩尺比精确模拟边界层湍流积分尺度，且无法测量杆件内力。更为精确的方法是从频域角度研究长横担输电塔的风振响应。悬臂结构的频域分析已有较多应用[10-12]。沈国辉等[11]利用时域和频域方法计算2个典型输电塔，认为长横担输电塔计算时需考虑高阶振型的影响；邓洪洲等[12]利用频域分析方法研究桅杆结构风振响应，发现利用SRSS法并考虑前5阶振型的贡献可以取得较为理想的结果。这些研究均需借助有限元软件和数学软件进行计算，计算过程较繁琐、不易纠错，且计算程序对结构的具体形式具有较强的依赖性，通用性较差。更为通用的方法是在有限元软件中直接进行频域分析，获得结构响应。本文采用ANSYS谱分析研究输电塔结构动力响应。首先，对比频域结果与时域结果，验证频域分析的准确性；其次，计算各阶振型对节点位移、节点加速度、杆件内力和基底反力均方根的贡献；最后，在考虑扭转振型贡献的基础上，计算扭转向等效静力风荷载，并将考虑扭转风荷载的杆件轴力与规范方法[5-6]和频域方法的杆件轴力进行对比。

1 输电塔ANSYS谱分析

1.1 ANSYS谱分析步骤

图1所示为ANSYS 频域分析步骤。由图1可见：ANSYS谱分析可分为有限元建模、模态分析、获得谱解及模态组合4 个步骤[13]。其中，前2 个步骤为常规模态分析，是为了获得结构的频率、振型向量、刚度及质量矩阵等信息。后2个步骤为谱分析，需对结构各加载点施加功率谱密度(PSD)激励，计算PSD 参与系数，并经PSD 模态组合获得结构响应的频域解。与结构频域分析[11-12]相比，模态分析和谱分析均在ANSYS中进行，模型数据具有更好的传承性；且利用APDL参数化有限元分析技术可使命令流具有更好的通用性。ANSYS 谱分析理论与经典随机振动频域分析理论[11-12]完全相同，具体公式推导可见文献[13]。

图1 ANSYS频域分析步骤Fig.1 Steps of frequency-domain analysis with ANSYS

1.2 输电塔模型及模态分析

以准东—华东±1 100 kV 特高压直线塔ZKC3010B2为研究对象。输电塔总高度为98.0 m，瓶口宽度为5.2 m，根开为20.2 m，呼高为87.0 m，横担部分总长度为55.0 m。风场类型为B类，设计风速为30 m/s。图2所示为采用beam188 单元建立的输电塔有限元模型。材料的弹性模量为2.06×1011N/m2，密度为10 205 kg/m3，泊松比为0.3。为了考虑实际工程中节点板、爬梯等附属结构质量的影响，材料密度取为钢材密度的1.3倍。塔脚处采用固定约束建立刚性支座。设输电塔垂直导线方向为90°方向(X向)，顺导线方向为0°方向(Y向)，竖直方向为Z向。本文没有采用塔线体系模型，这是因为输电塔的扭转效应及线对塔的影响程度均与风向角有关。0°风作用下结构的扭转效应最明显[3-4]，而0°风作用下塔线体系与单塔的振动特点及振动响应差别不大[3,14-15]。为简化计算，本文忽略了线对塔的影响，且仅研究0°风作用下的单塔响应。

图2 输电塔有限元模型Fig.2 Finite element model of transmission towers

首先，将塔身自重荷载、塔身平均风荷载及导线荷载简化的点荷载施加到结构上并进行静力分析，获得输电塔结构的初始构型；其次，利用分块Lanczos法对输电塔进行模态分析，分析结果如图3所示。输电塔1 阶模态为X向弯曲，2 阶模态为Y向弯曲，且1 阶和2 阶模态的频率较接近。输电塔3阶模态为Z向扭转，且扭平比为1.184，明显小于常规输电塔扭平比1.35的下限值[16]。这是因为受长横担的影响，结构扭转频率较低。

1.3 脉动风荷载谱的计算

输电塔风振计算属于线性多自由度体系的随机振动问题。ANSYS 谱分析中，需采用多节点力谱激励，即荷载为部分相关的脉动风力谱矩阵Sp(f)。矩阵中的任一项元素(f)为任意2 个加载点(m和n加载点)脉动风荷载pm(t)和pn(t)的互谱。由于0°(Y向)风作用下输电塔的扭转效应最明显[3-4]，脉动风荷载谱仅计算Y向加载点。另外，根据文献[6]的规定，各大风工况风荷载可由0°和90°风荷载组合得到。在90°风作用下，横担迎风面积最小，扭转效应最弱[3-4]，结构振动主要受到X向1阶弯曲振型的影响，其计算方法与常规输电塔相同。因此，本文不再研究90°风作用下的输电塔风振响应。图4所示为输电塔分段和风荷载加载点。由图4可见：全塔共分为24 个节段，风荷载加载点选为各节段主材和斜材的交点。

根据维纳-辛钦定理，(f)可通过对风荷载时程的乘积pm(t)⋅pn(t+τ)的期望进行傅里叶变换而得到：

图3 输电塔前6阶模态Fig.3 The first six modals of transmission tower

其中，加载点风力-风速关系可采用准定常理论[17]确定，m和n加载点荷载乘积可用式(2)表示：

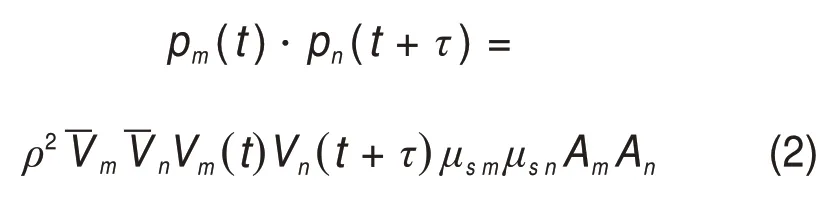
式中：ρ为空气密度；和分别为m和n加载点的平均风速；Vm(t)和Vn(t+τ)分别为m和n加载点处的脉动风速时程；τ为时间间隔；μsm和μsn分别为m和n加载点所在节段的体型系数；Am和An分别为m和n加载点的挡风面积，可由加载点所在节段总迎风面积除以该节段总加载点数而得到。

将式(1)和(2)联立，从而得到风力谱和风速谱的关系：

式中：(f)为m和n加载点风速的互功率谱，且

考虑风速空间相关性的影响，风速的互谱可表示为自谱与相干系数相乘的形式[17]：

式中：rmn为相干系数，这里采用SHIOTANI 等[18]提出的只与2 点距离有关的表达式，rmn=SV(f)采用归一化的Davenport 脉动风速谱来表示，SV(f)=K为地面粗糙度系数，为标准高度为10 m的平均风速，

风速与风压的相互关系和湍流度计算公式分别如式(5)和(6)所示：

式中：w0为基本风压；μzm和μzn分别为m和n节段风压高度变化系数；σVm和σVn分别为m和n点对应的风速均方根；Im和In分别为m和n节段对应的湍流度。

将式(1)～(6)联立，得到脉动风力互功率谱计算公式：

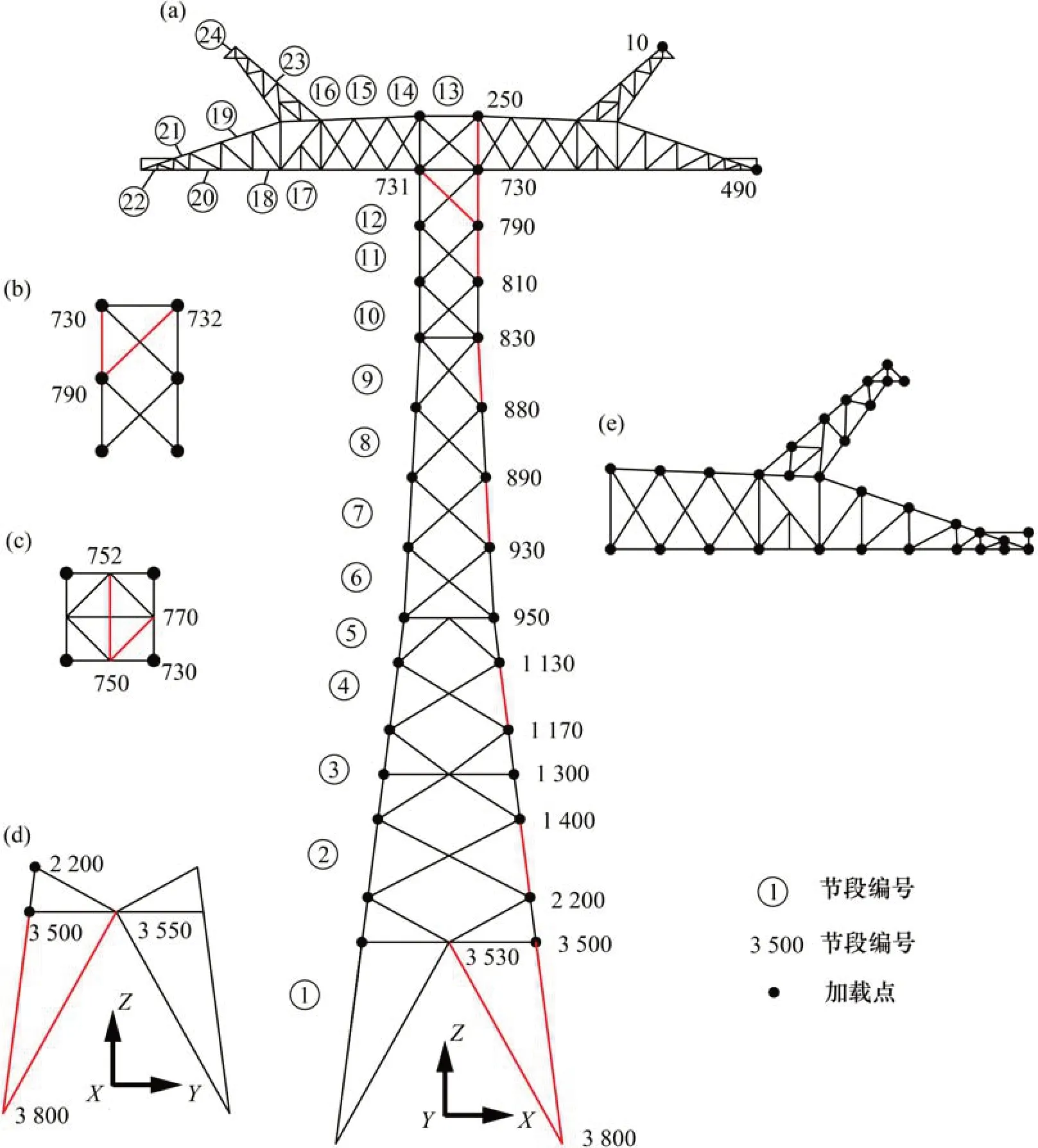
图4 输电塔分段和风荷载加载点Fig.4 Transmission tower subsections and the loading points of wind load

2 频域分析的验证

动力时程分析具有计算精度高和适用性广等优点，被广泛用于输电塔风振响应的研究[2-4,11,14,16]。因此，可以利用时域结果验证频域分析的准确性，结果如图5所示。时域分析采用与1.3 节完全相同的风速谱和相关函数，并利用AR法生成0°方向脉动风速时程。将风速时程与对应的加载点挡风面积、体型系数相联系，从而得到加载点0°方向(Y向)脉动风荷载并进行时程分析。时程分析的详细方法与文献[16]中的完全相同。

不同方法得到的节点位移功率谱密度曲线如图5所示。由图5可见：时域分析计算得到的功率谱曲线较为离散且具有一定的“毛刺”。频域分析得到的位移功率谱密度曲线较为平滑。为提高频域分析的准确性，模态组合包含了前20 阶振型的贡献。2种方法得到的功率谱密度曲线峰值所对应的频率较为一致，且与1.2节中的模态分析结果相同。2种方法得到的功率谱曲线峰值较为接近，仅在个别位置处略有差异且表现为时域峰值高于频域峰值。这是因为时域结果在转化过程中具有一定的离散性。整体来看，不同方法得到的功率谱密度曲线较接近，表明频域分析方法具有较高准确性。

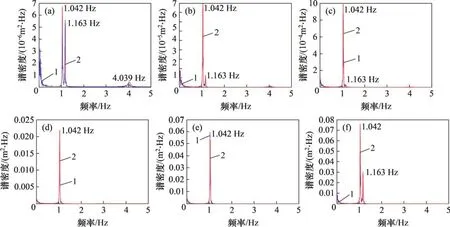
图5 节点位移功率谱时域和频域分析结果对比Fig.5 Comparison of power spectrum of joint displacements from time and frequency domain analysis

表1所示为节点位移均方根时域和频域分析结果对比。由表1可见：不同方法得到的节点位移均方根具有较好的一致性。对于塔腿及塔身下部节点，时域和频域均方根相差8%左右。对于变坡节点及塔身上部节点，时域和频域结果相差在2%以内。塔身下部节点位移误差稍大，这是因为塔身下部节点位移均方根的绝对值较小，较小的差值也会造成较大的相对误差。

综上所述，考虑前20 阶模态贡献的频域结果和时域结果具有较好的一致性，验证了ANSYS谱分析方法在输电塔风振响应研究中的可行性。

表1 节点位移均方根时域和频域分析结果对比Table 1 Comparison of RMS of joint displacements from time domain and frequency domain analysis

3 振型贡献分析

频域分析中参与组合的振型阶数越多，得到的结果就越精确，计算量也越大，因此，需在保证一定精度的条件下，确定频域分析的最少阶数。第2 节结果表明，前20 阶模态组合的频域结果与时程分析结果具有较好的一致性。现仅讨论前6阶振型对输电塔风振响应的贡献。0°方向风荷载不能激发输电塔X向振动，即X向振型(第1，4 和6 阶)对结构响应没有贡献。因此，图6所示为不同阶振型对结构响应的贡献百分比，即输电塔前2，3和5阶振型组合结果与前20阶振型组合结果的比值。

3.1 节点位移

如图5所示，不同节点的位移功率谱峰值所对应的频率不同。对于塔身下部节点(3 500)和节点(1 300)，位移主要由第2，3 和5 阶振型贡献。其中，低阶频率处峰值较高，高阶频率处峰值较低。高阶振型对位移的贡献随节点高度增加而降低。对于变坡节点(950)和节点(830)及横担主材处节点(730)，位移功率谱主要由第2阶振型贡献，高阶振型的贡献可以忽略。对于横担端部节点(490)，受输电塔扭转振动的影响，扭转振型有一定贡献。

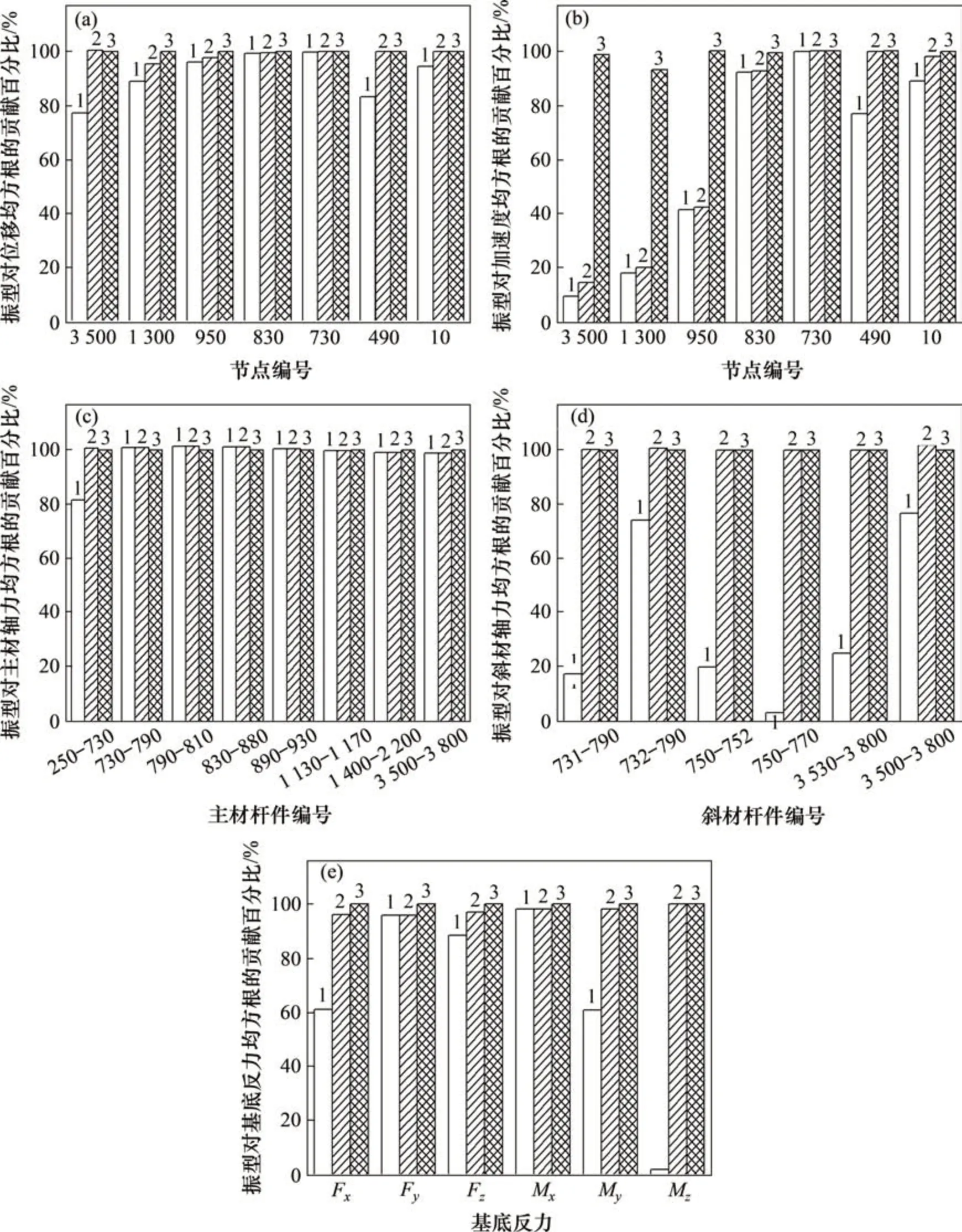
图6 振型对结构响应均方根的影响Fig.6 Influence of modes on RMS of structure response

振型对节点位移均方根的影响如图6(a)所示。对于塔身下部节点(3 500)和节点(1 300)，第2阶振型贡献在90%以下，考虑扭转振型的贡献后，位移响应均方根有较大幅度提高，与考虑前20 阶振型贡献的均方根相比误差在5%以内。表明扭转振型对塔身下部节点位移有10%～20%的贡献。对于1 次变坡节点及以上塔身节点，考虑前2 阶振型的位移响应为前20 阶振型的96%以上，加上扭转振型后，计算结果与前20 阶位移结果更加接近。对于横担端部节点(490)及地线支架节点(10)，扭转振型分别有约16%和5%的贡献。对于塔身节点位移响应，扭转振型的贡献随节点高度增加而减小；对于横担节点位移响应，扭转振型的贡献随节点与塔身轴线距离增加而增大。考虑前5阶振型贡献的位移均方根与考虑前20 阶振型贡献的位移均方根相同，说明前5阶振型可以完整地反映结构振动过程的位移响应。需要注意的是，前3阶频域结果有时会略大于20 阶频域结果，这是因为此节点处高阶振型的振型位移与低阶振型位移的方向相反。这一现象在(图6(b)～(e))中也出现，但这一影响较小，其振型贡献百分比接近于100%。

3.2 节点加速度

振型对节点加速度均方根的影响如图6(b)所示。对于塔身下部节点(950及以下节点)前2和前3阶振型的贡献低于50%。考虑前5 阶振型贡献后，加速度均方根占比显著增加，达到前20 阶振型加速度均方根的93%以上。说明塔身下部节点的加速度均方根受高阶振型(第5 阶)影响大。对于二次变坡及以上塔身节点，前2 阶振型的贡献达到92.42%以上。说明高阶振型对节点加速度均方根的贡献随高度增加而减小。对于横担端部节点(490)，扭转振型有约22.8%的贡献，而对于与横担端部节点相同高度处的塔身节点(730)，扭转振型的贡献仅为0.2%左右。说明扭转振型对横担节点加速度均方根的影响随节点与塔身轴线距离增加而增大。因此，第5阶振型对塔身下部节点加速度均方根影响较大，扭转振型对横担端部节点加速度均方根影响较大。

3.3 杆件轴力

振型对输电塔杆件轴力均方根的影响如图6(c)和图6(d)所示。对于塔头主材(250-730)，前2阶振型的贡献为81.62%，考虑扭转振型的贡献后，轴力均方根与前20 阶振型组合值基本相同。对于其他主材，第2阶振型对塔身主材轴力的贡献基本达到98%以上。第3和第5阶振型对主材轴力影响较小。这是因为结构的抗弯性能主要由主材提供，主材轴力在很大程度上受到输电塔弯曲振动的影响。对于塔身斜材，第2阶振型的贡献较低。如对于横担下隔面斜材(750-770)前2 阶振型的贡献率仅为3.3%。考虑扭转振型的贡献后，斜材轴力均方根与前20 阶振型轴力基本相同。说明扭转振型对斜材轴力的影响不可忽略。这是因为结构的抗扭刚度主要由斜材提供，结构的扭转振动会对斜材轴力产生较大影响。因此，文献[5-6]中仅考虑弯曲振型的方法，会造成斜材偏于不安全。

3.4 基底反力

振型对输电塔基底反力均方根的影响如图6(e)所示。第2 阶振型除对Y方向剪力、X方向弯矩和Z方向竖向力有较大贡献外，对其余方向基底反力的影响均较小。其中，对基底扭矩均方根的贡献仅为1.94%。当考虑扭转振型的贡献后，除Y方向剪力、X方向弯矩外，各基底反力的精度均有不同程度的提升。考虑第5阶振型贡献后，基底反力均方根的精度进一步提高。说明扭转振型对基底反力的影响不可忽略，更高阶振型对基底反力影响较小。

综上所述，0°(Y向)风荷载作用下，输电塔结构第2(Y向1 阶)、3(1 阶扭转)和5 阶(Y向2 阶)振型对结构振动有主要影响，更高阶振型的影响很小，可以忽略。

4 扭转向等效静力风荷载

4.1 扭转向静力风荷载计算公式

文献[5-6]中，顺风向风荷载计算公式以1 阶弯曲振型为主，无法考虑长横担输电塔风振过程中的扭转效应。本节参考文献[19]中提出扭转静力风荷载计算公式：

式中：Ti为i节段等效扭矩；为i节段转动惯量；为i节段角加速度均方根，可由ANSYS 谱分析得到；g为峰值因子，根据文献[5]取2.5。

输电塔结构的扭转效应主要由脉动风引起的非均匀脉动风力造成。由于塔身节段(①-○12节段)迎风面宽度小，相同高度2个加载点达到风速峰值的概率高，所引起的非均匀脉动风力不明显，结构产生的扭转向动力响应小。以⑧节段为例，塔身节段的角加速度均方根约为横担节段(图7)的25.43%。同时，由于塔身节段杆件围绕塔身轴线排列，塔身节段转动惯量较小。塔身⑧节段转动惯量约为横担节段的2.18%。由此可见，横担节段的扭转向静力风荷载占据主导地位，塔身节段扭转向静力风荷载可以忽略，因此，仅对横担部分进行扭转向静力风荷载计算。

图7 横担扭转分析模型Fig.7 Cross arm torsion analysis model

式(8)中，横担角加速度均方根的计算较为关键。图7所示为横担扭转分析模型，在0°风作用下，横担同时产生Y向平动位移、转动位移和弯曲变形产生的位移。设横担中心节段(节段)Y向位移为u1，端部节段(节段)Y向位移为u4，且u4可分解为横担转动产生的位移u2和弯曲变形产生的位移u3，横担长度的一半为L。其中，横担弯曲变形产生的位移u3较小，可以忽略[20]。则风荷载作用下t时刻及(t+τ)时刻的角加速度可表示为

式中：(t)和(t)分别为中心节段和横担端部节段的位移加速度；(t)为横担角加速度。

根据维纳-辛钦定理，横担转角加速度的自谱可通过对2个时刻转角加速度乘积的期望进行傅里叶变换得到，

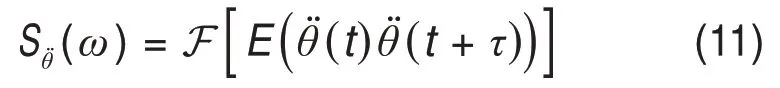
式中：(ω)为横担角加速度自谱。

将式(9)和(10)代入式(11)，并对横担节段位移加速度进行傅里叶变换：

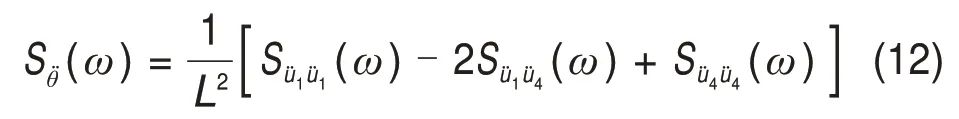
式中：(ω)和(ω)分别为横担中部节段及端部节段位移加速度自谱函数，(ω)为横担中部节段和端部节段位移加速度互谱函数，可由ANSYS谱分析直接得到。

根据随机振动理论，对角加速度谱进行积分并开方，得横担角加速度均方根

4.2 杆件轴力分析

为验证扭转向静力风荷载计算公式的适用性，将本文方法、文献[5-6]中方法、有限元频域方法得到的杆件轴力进行对比分析，结果如图8所示。文献[5-6]中等效风荷载主要考虑了第2 阶振型(Y向1 阶弯曲)的贡献，式(8)主要考虑了第3 阶振型(1 阶扭转)的贡献。虽然第5 阶振型(Y向2 阶弯曲)对塔身节点的加速度有较大影响(图6(b))，但主要影响一次变坡节点及以下节点。考虑第5阶振型影响后，塔身下部节段的静力风荷载增加明显，但由于下部节段高度较低，对塔身产生的弯矩作用较小，因此，本文不分析考虑第5阶振型贡献的杆件轴力。

频域方法杆件轴力P1按式(14)计算；本文杆件轴力P4按式(15)计算，由扭转静力风荷载作用下的杆件轴力和文献[6]中的杆件轴力相互叠加得到，这是由于扭转向静力风荷载和文献[6]顺风向静力风荷载均由顺风向风荷载产生。为对比不同方法杆件轴力的计算结果，需将扭转向静力风荷载和顺风向静力风荷载的计算结果叠加。

式中：P1为频域方法杆件轴力；Pmean为平均风作用下杆件轴力，平均风荷载按文献[6]进行计算时风振系数取为1；σP为有限元频域分析得到的杆件轴力均方根；P4为本文方法得到的杆件轴力；P3为按文献[6]中方法计算得到的杆件轴力；PT为等效扭转风荷载(式(8))作用下的杆件轴力。

下面以具有一定保证率的杆件轴力统计值P1为标准进行对比(图8)，若P3或P4比P1大，则杆件轴力时程超过P3或P4的概率就小，也就是说保证率高，相反则保证率低。不同等效风荷载计算方法得到的杆件轴力与频域方法杆件轴力P1的比值如图8所示。与文献[5]方法得到的杆件轴力(P2)相比，文献[6]计算得到的杆件轴力(P3)较接近，且均略小于P2。这是因为文献[6]考虑了风速水平相关性的影响，导致横担风荷载略小于文献[5]中风荷载。与频域方法相比，文献[6]得到的主材轴力除横担处塔身主材(250-730)外均偏大2.2%左右，斜材轴力则偏小较多，最大偏小92.5%(750-770)。在文献[6]方法上叠加扭转静力风荷载(式(8))后，主材轴力略有提升，且提升幅度在6%以内(与文献[6]相比)，斜材轴力得到较大提升，与频域方法相比大0.1%～15.8%。考虑扭转向静力风荷载后，斜材轴力的保证率得到较大提高。这是因为输电塔抗扭刚度主要由斜材提供。等效扭转风转以扭矩的形式作用到结构上，并主要体现在斜材轴力上。

图8 杆件轴力对比Fig.8 The comparison of axial force acting on members

因此，文献[5-6]所提出的方法对主材具有较高的保证率，而对斜材的保证率较低。本文方法在文献[6]的基础上增加了等效扭矩的作用，在不明显提高主材轴力的基础上，有效提升了斜材杆件的保证率。需要说明的是，由于文献[6]中方法专业性更强，这里采用文献[6]中杆件轴力和等效扭转静力风荷载组合作用下的杆件轴力作为本文方法杆件轴力，如式(15)所示。若采用文献[5]中杆件轴力进行计算(式(15)中P3换为P2)，所得结论是一致的。

5 结论

1)时域方法和频域方法得到的位移功率谱密度曲线、节点位移均方根吻合较好，说明有限元频域分析方法适用于求解输电塔结构的顺风向风致响应且具有较高的精度。

2)输电塔结构的第3 阶振型(1 阶扭转)对塔身下部及横担端部节点位移、横担端部节点加速度、塔头及塔身斜材轴力和基底反力影响较大；第5阶(Y向2阶)振型对塔身下部节点加速度有较大影响；更高阶振型对结构的影响很小，可以忽略。

3)与频域方法相比，得到的主材轴力偏大2.2%左右，斜材轴力偏小16.1%～92.5%，说明规范方法对主材轴力有较高的保证率，对斜材轴力的保证率较低。

4)与频域方法相比，主材轴力偏大6.1%～8.6%，斜材轴力偏大大0.1%～15.8%，说明本文方法在不明显增大主材轴力的基础上，有效提高了斜材的保证率，具有较好的适用性。