球状物体运动的检测与轨迹跟踪∗

孔 秀 史金龙 高 璐

（江苏科技大学计算机学院 镇江 212003）

1 引言

近年来，计算机科学发展迅猛，视觉图像［1］作为人类接收信息的主要途径受到了诸多关注。随着发展的进步，基于立体视觉技术［2］的研究也越来越深入，并广泛地应用到了生活的各个领域。如体育竞技、数字化城市与三维地图、医疗中的影像分析、航空中的卫星图片、古代建筑三维数字化保护、VR&AR游戏、电影等［3］。

在球类比赛中，仅仅利用肉眼观测和经验推断，已经不能满足于体育竞技的现阶段要求。利用数字图像技术检测球类运动，并对运动轨迹进行跟踪，能辅助教练与运动员进一步了解球的运动趋势、速度和落点，从而制定改进的技术策略和训练方案，进一步提升训练效果。运动检测与轨迹跟踪［4］是计算机视觉中的研究重点，其过程是利用两台摄像机得到运动视频序列，根据目标的特征来检测匹配，从而获取运动目标的三维运动序列，实现轨迹跟踪。近些年，研究人员对于球类运动轨迹的跟踪提出了一些观点。文献［5］利用斯诺克的颜色特征跟踪彩球的运动轨迹，颜色特征是体育视频分析中运用广泛的特征之一。除此之外，国防科技大学提出基于语义单元（BSU）的视频分割方法［6］，利用颜色特征进行场景检测；而文献［7］则通过分析视频对象的运动轨迹和相互运动关系分割足球比赛视频［8］。

通过上述分析可以看出，体育视频的内容复杂又多样，目前体育视频分析结果还不很理想，整个体育视频分析仍处于初步研究阶段。本文旨在提出一种针对于球状物体运动的检测识别和轨迹跟踪的研究方法。以乒乓球为实验对象，建立一套双目运动捕捉系统［9］，对运动中的乒乓球进行检测和轨迹跟踪，获取球体的运动轨迹、落地点和不同时刻的运动速度，从而进行下一步的轨迹预测。利用标定好的两台摄像机拍摄乒乓球的运动过程，获取视频序列并将视频逐帧分解，通过椭圆拟合方法从不同帧中检测到乒乓球的位置。考虑到类似于斯诺克中球类颜色的多样性，本文提出利用颜色来区分不同乒乓球目标。除此之外，当球类不存在明显的纹理特征或者颜色特征时，利用物理特征［10］进行跟踪的方式将不再适用，而传统光流［11］不能够对运动速度较快的乒乓球进行捕捉跟踪。本文利用改进的大尺度光流跟踪［12］的方法对运动目标进行轨迹跟踪，避免了由于位移过大产生的跟踪错误和丢失问题。最后将不同时刻的目标位置信息整合，利用非线性曲线拟合技术得到目标运动轨迹。结合三维轨迹数据，对目标的运动进行分析，从而获取更多有效的物理信息。

2 目标检测与匹配

如图1（a）所示，实验器材为两台索尼FDR-AX30 相机。实验环境选在具有充分光源的室内，三脚架间距约20cm 平行放置，高度与焦距校准。如图1（b）、图1（c）所示，实验对象分为彩色组与白色组，每组各有6只大小均匀的乒乓球。

图1 实验器材及实验对象

实验进行前，需要对两台相机进行标定，这里采用张正友标定法［13］。标定获得相机的内外参数矩阵KL,KR,R,T，以及畸变系数DL,DR，以左相机为世界坐标系的原点，标定结果如下所示：

2.1 目标检测

由于乒乓球在二维平面上呈现为圆形，且快速运动过程中会产生一定的形变，传统的特征检测算法不易获取有效特征。本文采用最小二乘法拟合椭圆［14］对乒乓球进行目标检测，拟合后获取乒乓球的球心坐标。

椭圆方程是一种特殊形式的二次曲线，可以使用式（1）表述为

在式（1）中，a，b，c，d，e 是椭圆系数，(xi,yi)(i=1,2,3,…,n)为椭圆轮廓上的n（n≥5）个测量点坐标。最小二乘法的原理是使得测量拟合误差的平方和最小化，由此所拟合的目标函数为式（2）：

利用奇异值分解法解出方程系数a，b，c，d，e的值。根据椭圆的相关几何知识，可以获得椭圆的各个位置参数，包括二维图像上的圆心坐标。

图2 椭圆拟合前后对比

图2 为彩色实验组椭圆拟合前后对比效果。可以看出，该方法能够精准地对目标乒乓球进行检测拟合，满足实验要求。表1 为椭圆拟合检测到的本帧上6颗乒乓球的球心位置。

表1 乒乓球球心二维坐标

2.2 匹配左右图像圆心

完成目标检测之后，需要进行目标点在左右视图上的匹配。使用立体校正将非共面行对准的两幅图像校正成共面行对准。利用极线约束［15］将左右匹配由二维搜索降为一维搜索以减少匹配搜索范围。

本文提出一种将立体校正与欧氏距离相结合对左右图像上的球心进行匹配的方法。假设三维空间中存在点C（x，y，z），其在投影在左视图上为Cl（xl，yl），投影在右视图上为点Cr（xr，yr）。经过立体校正，Cl与Cr处于同一极线，寻找左视图上点Cl在右视图上的匹配点Cr，只需在对应极线上进行搜索。已知左右视图在水平方向上的坐标差值为Δx，推算出Cl在右图上的映射点Cl-r（xl+Δx，yl）。同一行上存在部分备选匹配点P1，P2，…，Pn，使用式（3）所示的欧氏距离方法剔除噪声点，找出正确匹配点Cr。

分别计算点Cl-r与各个备选点之间的欧氏距离d，d 值最小者为最优匹配点Cr。连接左右匹配点，效果如图3所示。

由匹配结果可以看出，本文提出的立体校正与欧氏距离相结合的匹配方法，匹配精准度较高。

经过椭圆拟合进行目标检测、立体校正与欧氏距离结合进行左右球心匹配后，左右图像上对应球心的二维坐标均可获得。由标定时得到的相机内外参数，经三角测量法［16］可以将二维图像坐标转化为三维空间坐标。完成球心在空间上的重建，能够立体的看到每颗乒乓球在不同帧上的不同位置。如图4 所示，不同时刻6 颗球在同一帧上的运动位置。图4（a）为该时刻摄像机拍摄到的乒乓球运动位置，图4（b）为通过三维重建获取的空间球心点在三维坐标中的位置。

3 目标跟踪

对左右视图中各个目标圆心点匹配后，为了获取动态目标的运动轨迹，还要在前后帧时间序列上对目标进行跟踪。

3.1 基于颜色特征的目标跟踪

由于实验环境具有较为稳定光源，当实验对象为具有颜色特征的彩色乒乓球时，可以利用颜色特征对前后帧图像上的球心进行目标跟踪。前文通过椭圆拟合获得左右图像上的球心序列。取前一帧图像上某一颗乒乓球的球心坐标，并得出该坐标点在图像上呈现的RGB 值，由此判断该球的颜色类别。考虑到光照和周围环境对乒乓球色彩的影响，不同颜色的乒乓球RGB 值在一定的范围内波动。通过后一帧图像上的球心坐标序列，在后一帧图像上寻找与之最为接近的RGB 值，即颜色特征相似，跟踪成功。如组图5 所示，连续30 帧中左图像上跟踪的彩色乒乓球的RGB值变化趋势。

图5 连续30帧球心的RGB变化

从组图5 中数据可以看出，连续帧之间乒乓球颜色的RGB值差距甚微。在进行跟踪时，先利用R值进行判断色彩，当球心的R值不足以区分颜色时结合G 值和B 值，可以准确地对球心色彩进行分类。由此可以完成彩色乒乓球的目标跟踪。如图6所示为基于颜色特征所跟踪到的6颗彩色乒乓球在连续两帧间的运动方向示意图。

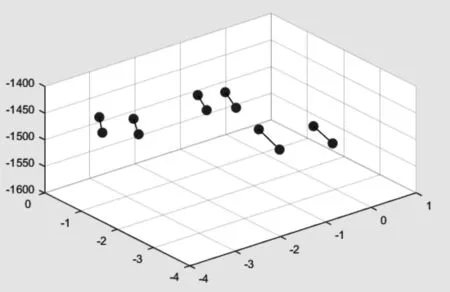
图6 连续两帧乒乓球运动示意图

3.2 基于光流法的目标跟踪

当乒乓球不具有明显的颜色特征作为跟踪根据时，本文融合了大尺度光流算法和SIFT 方法，在传统变分光流模型［17］中加入相似描述符的约束，结合使用前后帧对应点最小位移差，从而有效地跟踪目标。

设待跟踪的连续两帧图像分别为第I、I+1 帧，跟踪步骤如图7所示。

图7 获取光流值过程图

重复以上过程，直至获得I 帧和I+1 帧图像的最后一层的光流值为止。令数组F 存有图像上每个像素点的光流值。以获得的I帧图像上某个圆心坐标PI（px，py）为计算值，经光流数组F 在I+1 帧图像上找到其对应点PI+1坐标为（F［px］［py］［1］，F［px］［py］［2］）。继而以点PI+1跟踪到I+2帧上的点PI+2……由此完成连续帧之间目标圆心点的跟踪。

由于实验环境复杂且跟踪的目标对象为物理特征不明显的乒乓球，实验过程中有可能会出现部分跟踪失误。本文所用相机帧率为25帧/s，则目标乒乓球在连续的前后两帧之间的运动极其微小，同一个乒乓球在连续两帧之间的球心位移变化波动微弱，所以在连续前后帧之间运用最小欧氏距离进行点的跟踪判断。

假设第N 帧上i个圆心点均跟踪到N+1帧上的圆心点（xn+1，yn+1），定义N 帧上i 个点的坐标为（xin，yin）（1≤i≤6），在N+1 帧上进行跟踪搜索。利用式（4），i个疑似点中与点（xn+1，yn+1）距离Δd最小的即为正确跟踪点。

由基于光流法跟踪到一颗乒乓球在连续17 帧间的运动情况如图8 所示，由跟踪图可以明显看出乒乓球的下落弹跳运动。

4 轨迹重建与分析

由目标跟踪获得乒乓球运动过程中球心的三维坐标序列，可以利用Matlab 中的plot3 函数拟合出其运动轨迹。

如图9所示为6只球在空间中的运动轨迹。实验中，乒乓球上抛后自由下落，触及水平桌面后进行弹跳运动，直至停止。从图中可以明显看出乒乓球的弹跳运动轨迹。

图8 乒乓球在连续17帧间的运动示意图

图9 乒乓球运动轨迹

根据运动轨迹和相关数据，获得乒乓球运动下落点、速度的变化，由此得知乒乓球的运动状态。一颗乒乓球在30 帧图像内落点3 次的空间位置分析结果如表2所示。

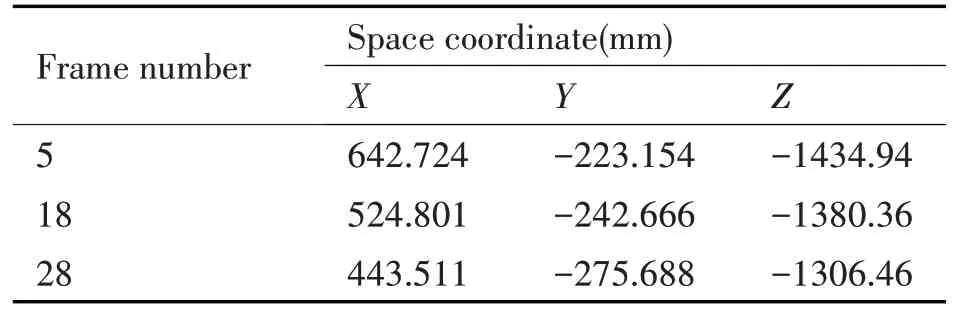
表2 乒乓球的落点位置变化

相机帧率为25帧/s，则连续两帧之间的时间间距为0.04s。利用式（5）可以求出乒乓球球心在不同帧的瞬间速度v。

乒乓球在不同帧的瞬时速度为表3所示。

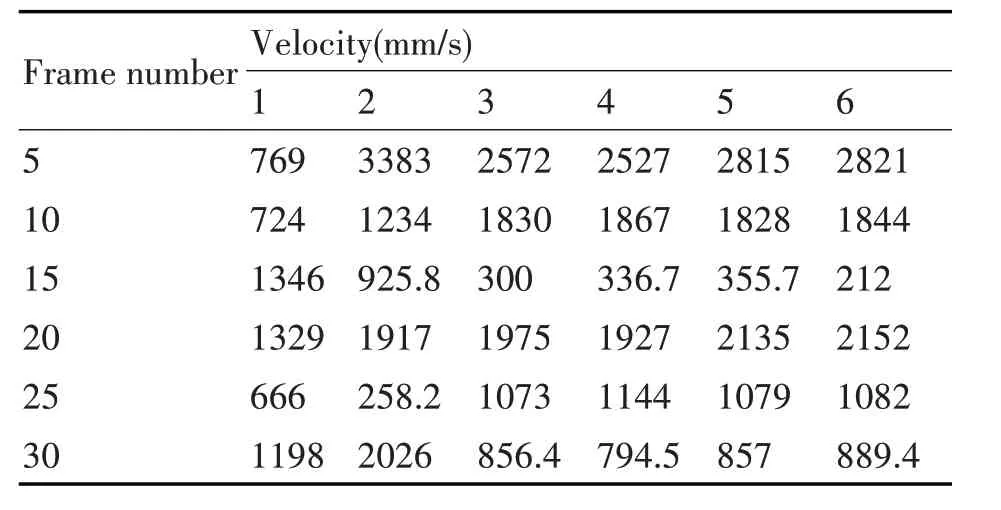
表3 乒乓球的瞬时速度变化

5 结语

本文基于图像三维重建系统，研究球状物体运动的轨迹追踪。使用椭圆拟合检测获取图像上的球心，将立体校正和欧氏距离相结合完成左右视图上对应球心的匹配。分别利用色彩特征和光流算法对乒乓球进行跟踪，继而重建各个目标点的三维数据，形成球状物体的运动轨迹。经过实验验证，该方法复杂度低、稳定可靠，在今后仍有很好的研究和应用价值，适用于球类体育竞技比赛及相关行业中。