Re(q)群与区传递4-设计

曾玲玲 龚罗中

（1.长沙师范学院 图书馆，湖南 长沙 410100；2.长沙师范学院 数学科学学院，湖南 长沙 410100）

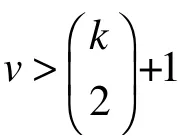
主要定理：设D 是一个4-(v,k,1)设计，群G 是D 的一个区-传递、点-本原的自同构群，若v 为奇数，则G 的基柱 X= Soc (G)不能是Re(q)群。

1 预备引理

设D 表示一个4-(v,k,1)设计，G 是D 的一个区传递，点-本原的自同构群。X 是群G 的基柱Soc(G)，Gα是点α∈Ω在G 内的点稳定子群， GB是区组B ∈ Q在G 内的区稳定子群。如下的引理是证明主要定理的基本信息。

引理1.1[11]设D=(Ω,Q)是一个t-(v,k,λ)设计，对于一个正整数s≤t，设S⊆Ω，且S = s。则包含S 中的每个元素的区组数为：

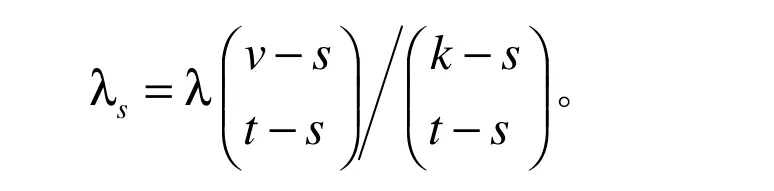
特别的，对于t≥2，一个t-(v,k,λ)设计也是一个s-(v,k,λs)设计。

若用 1: λ=r 表示包含一个给定点的区组数，我们有下面的推论。

推论1.2 设D 是一个4-(v,k,1)设计，则下列结论成立：

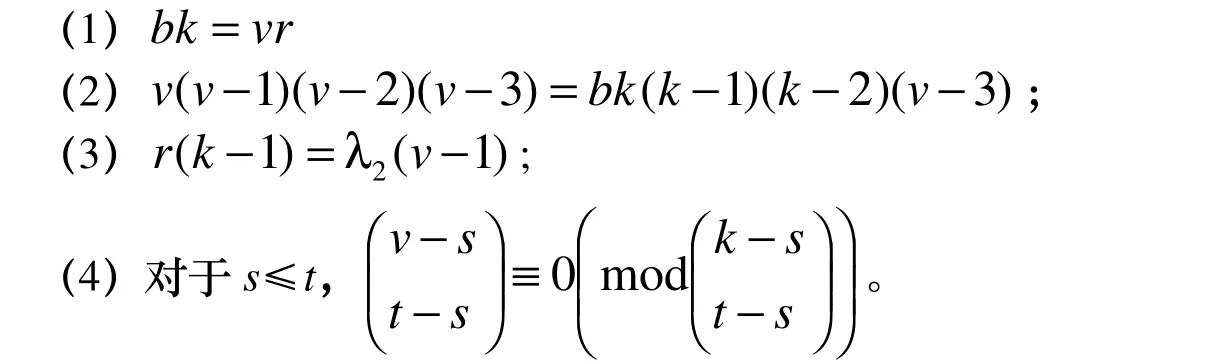
引理1.3[12]设G 是一个奇数阶集合Ω上的本原置换群。假设G 的基柱 X = X(q)，是一个有限域GF (q)上的例外李型群，且 Gα是点α∈Ω在G 中的稳定化子，那么如下的结论成立：

（1）如果q 是偶数，则 X ∩ Gα是X 的一个抛物子群；

（2）如果q 是奇数，则下面的结论之一成立；

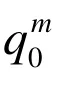
(ii)X 是一个例外李型群，X 和 Gα的特征是已知的。

特别地，当 X = Re( q)时， Gα= 2 × PSL2( q),X ∩ Gα= q ( q2− 1)。

命题1.4[13]如果D 是一个非平凡的steiner-t 设计，那么如下的结论成立：

（1） v ≥ ( t + 1)( k − t+ 1);

（2） v − t + 1 ≥( k − t + 2)( k − t + 1)， t >2。

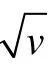
证明: 由命题1.4(2)知

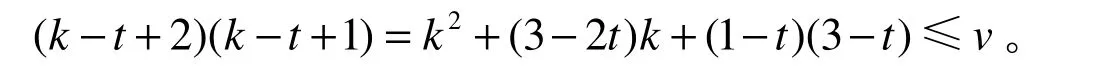
整理得 k2+ (3 − 2 t ) k + (1 − t )(3 − t ) − v ≤0。因为t >2，故当t =2 时，k 可取得最大值。此时有 k2− 3k − v ≤0。

由二次函数的性质可知，

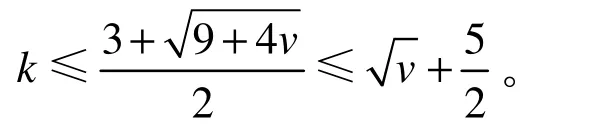
2 主要定理的证明

假设G 的基柱 X= Soc (G)是 Re(q )群2G2( q )，则 q = 32c+1>3。我们知道 Aut( X )=Re(q)×:<α>，这里 × :表示半直积，α 表示一个阶为 2 c +1Frobenius 自同构 GF (q)→GF(q)，x ax3.因此，由Dedekind's 定理可得， G =Re( q )×:(G ∩<α>)，从而

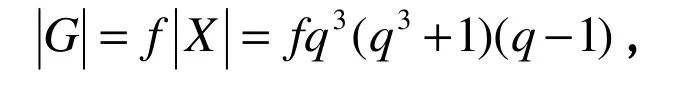
这里|G ∩< α>|= f 2 c+ 1。

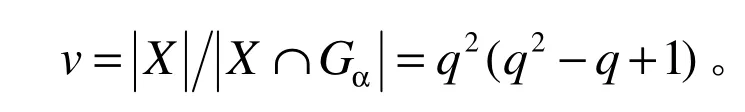
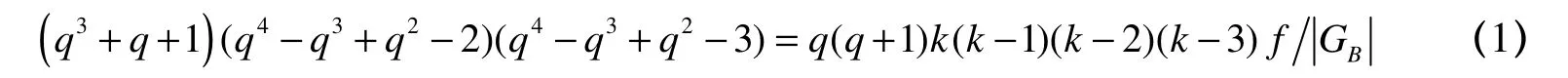
我们先来证明对于任意的 g∈ G，如果稳定三个不同的点，必定稳定四个点。设FixX(g)=3，x∈ FixX(g)，P 是 Re( q )x的正规Sylow-3 子群，正则的作用在 X {x}。如果 y, z ∈FixX(g){x}，则z= yh，h ∈ P。因此， yhg= yg=yhg，于是有

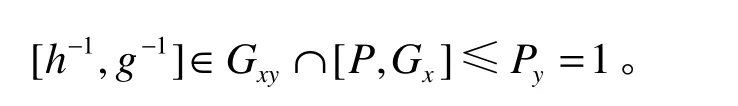
从而， h ∈ CP(g),因此 C（Pg )在 FixX(g ){x}上点传递，故FixX(g)≡0(mod2)，自然有FixX( g) ≥ 4。因为G 是区传递的，我们可以将讨论限定在一个包含3-子集 { 0 ,1,∞} 的区组B 上。由上面的讨论，我们有 Aut (X)0,1,∞=<α>。因此， G ∩< α>≤ GB，故f GB≤ 1。再由式(1)得

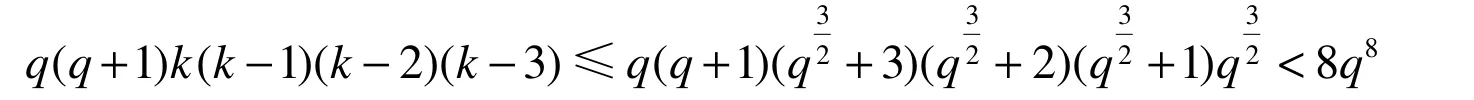
因为 q = 32c+1>3。同样因为 q = 32c+1>3，有

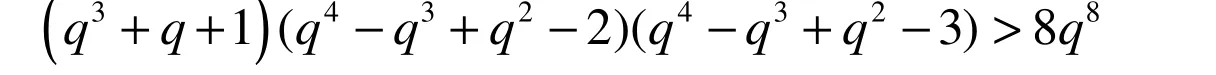
这与式(2)矛盾，这就完成了主要定理的证明。

3 结 语

区传递4-设计的分类是目前组合设计分类工作中的一个非常难处理的问题，而有限单群分类定理（将单群分为：素数阶循环群；n≥5 的交错群；Lie型单群(共16 族)；26 个散在单群）是组合设计分类的基本理论依据。本文对上述的Lie型单群中的Re(q)群讨论Steiner 4-设计分类，运用的方法具有一般性，可以类似地推广到讨论其他的Lie型自同构群族。