四元数群到一类10pn阶非交换群的同态数量
李凤娇, 高百俊
(伊犁师范大学 数学与统计学院, 新疆 伊宁 835000)
0 引 言
群之间同态数量满足的同余关系是群论研究的基本问题之一. 文献[1]给出了n阶循环群到有限群同态个数满足的同余方程; 文献[2]将n阶循环群换成了有限交换群, 推广了文献[1]的结果; 文献[3]去掉了群的交换性, 推广了文献[2]的结果, 并提出了Asai和Yoshida猜想; 文献[4-6]研究了一些有限群之间的同态个数; 文献[7-8]计算了群同态个数, 并验证了所研究的群满足Asai和Yoshida猜想; 文献[9]计算了四元数群与一类亚循环群之间的同态个数, 并验证了四元数群和这类亚循环群满足Asai和Yoshida猜想. 本文考虑以一类Sylowp-子群为循环群的10pn阶非交换群, 构建四元数群到该类10pn阶非交换群的同态映射, 并计算其同态个数, 验证这两类群满足Asai和Yoshida猜想.
为叙述方便, 先给出两个群的结构: 设m是正整数且m≥2, 如果
Q4m=〈x,y|x2m=1,xm=y2,xy=yx-1〉,
(1)
则称群Q4m为4m阶的四元数群. 设p是大于5的素数, 令
G10pn=〈a,b|a10=1=bpn,ba=ab-1〉,
(2)
由文献[10]知G10pn是一类Sylowp-子群为循环群的10pn阶非交换群. 本文中φ表示Euler函数, 其他记号可参见文献[11].
1 预备知识
引理1设G10pn满足式(2),p是大于5的素数, 则〈a〉∩〈b〉=1.
证明: 由循环群的定义及Lagrange定理可知〈a〉∩〈b〉=1.
引理2设G10pn满足式(2),p是大于5的素数, 则:
1) {a5bj|0≤j 2) {ai|i=2,4,6,8}为G10pn中所有的5阶元且为G10pn的中心元; 3) {aibj|i=1,3,7,9, 0≤j 证明: 1) 设o(aibj)=2, 其中0≤i<10, 0≤j (aibj)2=a2ib2j=1, 由引理1知a2i=1且b2j=1. 于是i=0,j=0, 与o(aibj)=2矛盾. 因此{a5bj|0≤j 2) 设o(aibj)=5, 其中0≤i<10, 0≤j 任取akbl∈G10pn, 其中0≤k<10, 0≤l aiakbl=ai+kbl=akblai. 因此ai(i=2,4,6,8)为G10pn的中心元. 3) 设o(aibj)=10, 其中0≤i<10, 0≤j 引理3设G10pn满足式(2),p是大于5的素数, 则: 2)o(aibj)=[5,o(bj)], 其中i=2,4,6,8, 0 证明: 1) 由有限群元素阶的性质易得结论. 2) 由引理1和引理2中2)易得结论. 引理4设Q4m为4m阶四元数群, 则〈x〉∩〈y〉=1或y2. 证明: 假设〈x〉∩〈y〉≠1. 若xi=y, 则由xy=yx-1可得xxi=xix-1, 即x2=1, 与o(x)=2m矛盾. 若xi=y2, 则由xy=yx-1可得 xi+1y-1=xi+1y-1, 再由xm=y2可知i=m. 若xi=y3, 则由xy=yx-1可得 xxiy-2=xiy-1x-1, 即x2=1, 与o(x)=2m矛盾. 因此〈x〉∩〈y〉=y2. 定理1设m是正整数且m≥2,p是大于5的素数. 若m是偶数且5|m, 则: 1) 当p|m时, |Hom(Q4m,G10pn)|=2pn+pn+k+1, 这里k是正整数且0 |Hom(Q4m,G10pn)|=3pn+1. 证明: 设θ∈Hom(Q4m,G10pn), 因为(y4)θ=(yθ)4=1, 所以o(yθ)|4. 又yθ∈G10pn, 于是o(yθ)|(10pn), 从而o(yθ)|(10pn,4), 即o(yθ)|2. 因此yθ∈{1}∪{a5bj|0≤j 1) 当p|m时, 令m=pil, 其中(p,l)=1, 再令k=min{n,i}, 则(10pn,2m)=10pk, 因此o(xθ)|(10pk). 若xθ=bj, 则 (xθ)pn=(bj)pn=(bpn)j=1, 于是o(xθ)|pn, 从而o(xθ)|pk. 若xθ=aibj, 则 (xθ)5pn=(aibj)5pn=1, 于是o(xθ)|(5pn), 从而o(xθ)|(5pk). 又由引理2可知 下面分8种情形证明. 任取xsyt∈Q4m, 其中0≤s<2m, 0≤t<2, 令(xsyt)θ=(a5bj)s. 设xs1yt1,xs2yt2∈Q4m, 若xs1yt1=xs2yt2, 则xs1-s2=yt2-t1∈〈x〉∩〈y〉=1或xm, 于是2m|(s1-s2)或2m|(s1-s2-m). 由引理2中1)可知(a5bj)s1-s2=1, 从而(a5bj)s1=(a5bj)s2, 即(xs1yt1)θ=(xs2yt2)θ, 因此θ为映射. 任取xs1yt1,xs2yt2∈Q4m, 当t1=1时, 易得(xs1yxs2yt2)θ=(a5bj)s1-s2, 且 (xs1y)θ(xs2yt2)θ=(a5bj)s1+s2. 由引理2中1)可知(a5bj)2s2=1, 于是(a5bj)s1-s2=(a5bj)s1+s2, 从而 (xs1yxs2yt2)θ=(xs1y)θ(xs2yt2)θ, 即θ为群同态; 当t1=0时,θ显然为群同态. 在此情形下群同态θ有pn种选择. 若θ∈Hom(Q4m,G10pn), 则由xy=yx-1可得 aibj=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=(aibj)-1, 即(aibj)2=1, 矛盾. 故此时群同态θ不存在. 必要性. 若θ∈Hom(Q4m,G10pn), 首先由xy=yx-1可得 bj=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=b-j, 即b2j=1, 从而j=0; 其次由xm=y2可得 bmj=(xθ)m=(xm)θ=(y2)θ=(yθ)2=1, 即o(bj)|m, 又由已知条件可知o(bj)|m成立. 因此当θ为群同态时,j=0. 充分性. 当j=0时,θ显然为平凡同态. 在此情形下群同态θ有1种选择. 由情形②的证明可知情形④成立. 必要性. 若θ∈Hom(Q4m,G10pn), 首先由xy=yx-1可得 bj-i=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=bi-j, 即b2(j-i)=1, 从而i=j; 其次由xm=y2且m是偶数, 易得(a5bj)m=1. 因此当θ为群同态时,i=j. 充分性. 任取xsyt∈Q4m, 其中0≤s<2m, 0≤t<2, 因为i=j, 所以令(xsyt)θ=(a5bj)s(a5bj)t. 设xs1yt1,xs2yt2∈Q4m, 若xs1yt1=xs2yt2, 则xs1-s2=yt2-t1∈〈x〉∩〈y〉=1或y2=xm, 于是2m|(s1-s2)且4|(t2-t1)或2m|(s1-s2-m) 且4|(t2-t1-2). 由引理2中1)知, (a5bj)s1-s2=1=(a5bj)t2-t1. 因此(xs1yt1)θ=(xs2yt2)θ, 故θ为映射. 任取xs1yt1,xs2yt2∈Q4m, 当t1=1时, 易得 (xs1yxs2yt2)θ=(a5bj)s1-s2(a5bj)t2+1, 且 (xs1y)θ(xs2yt2)θ=(a5bj)s1+s2(a5bj)t2+1, 由引理2中1)可知(a5bj)2s2=1, 于是 (a5bj)s1-s2(a5bj)t2+1=(a5bj)s1+s2(a5bj)t2+1, 从而 (xs1yxs2yt2)θ=(xs1y)θ(xs2yt2)θ, 即θ为群同态; 当t1=0时,θ显然为群同态. 在此情形下群同态θ有pn种选择. 若θ∈Hom(Q4m,G10pn), 则由xy=yx-1可得 a5+ibh-j=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=a5-ibj-h, 即a2ib2(h-j)=1, 由引理1知此i不存在, 故此时群同态θ不存在. 由情形⑥的证明可知情形⑧成立. 综上可知, 当p|m时, |Hom(Q4m,G10pn)|=2pn+pn+k+1. xθ∈{1}∪{a5bj|0≤j 下面分8种情形证明. 显然此时θ为群同态, 且群同态θ有1种选择. 任取xsyt∈Q4m, 其中0≤s<2m, 0≤t<2, 令(xsyt)θ=(a5bj)t. 设xs1yt1,xs2yt2∈Q4m, 若xs1yt1=xs2yt2, 则xs1-s2=yt2-t1∈〈x〉∩〈y〉=1或y2,于是4|(t2-t1)或4|(t2-t1-2). 由引理2中1)可知(a5bj)t2-t1=1, 即(xs1yt1)θ=(xs2yt2)θ, 因此θ为映射, 且θ显然为群同态. 在此情形下群同态θ有pn种选择. 由定理1中1)的情形①,⑤可知, 上述两种情形均成立, 且群同态θ有pn+pn=2pn种选择. 若θ∈Hom(Q4m,G10pn), 则由xy=yx-1可得 ai=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=a-i, 即a2i=1, 由已知条件可知此i不存在, 故此时群同态θ不存在. 若θ∈Hom(Q4m,G10pn), 则由xy=yx-1可知 a5+ibj=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=a5-ibj, 即a2i=1, 由已知条件可知此i不存在, 故此时群同态θ不存在. 由定理1中1)的情形②,⑥可知上述两种情形均成立. 证明: 设θ∈Hom(Q4m,G10pn),yθ的选取方式同定理1. 因为(x2m)θ=(xθ)2m=1, 所以o(xθ)|(2m). 又因为o(xθ)|(10pn), 从而o(xθ)|(10pn,2m). 1) 当p|m时, 令m=pil且(p,l)=1, 再令k=min{n,i}, 则(10pn,2m)=2pk, 因此o(xθ)|(2pk). 若xθ=bj, 则 (xθ)pn=(bj)pn=(bpn)j=1, 于是o(xθ)|pn, 从而o(xθ)|pk. 若xθ=aibj, 则 (xθ)5pn=(aibj)5pn=1, 于是o(xθ)|(5pn), 从而o(xθ)|pk. 又由引理2中1)知, 下面分6种情形证明. 由定理1中1)的情形①~③,⑤~⑦可知上述情形均成立. 综上可知, 当p|m时, |Hom(Q4m,G10pn)|=2pn+pn+k+1. 下面分4种情形证明. 由定理1中1)的情形①,⑤可知上述两种情形均成立. 由定理1中2)的情形①,②可知上述两种情形均成立. 定理3设m是正整数且m≥2,p是大于5的素数. 若m是奇数且5|m, 则: 1) 当p|m时, |Hom(Q4m,G10pn)|=1+pn+k, 这里k是正整数且0 证明: 设θ∈Hom(Q4m,G10pn),yθ的选取方式同定理1. 1) 当p|m时,xθ的选取方式同定理1中1). 下面分8种情形证明. 若θ∈Hom(Q4m,G10pn), 由xm=y2可得 (a5bj)m=(xθ)m=(xm)θ=(y2)θ=(yθ)2=1. 又m是奇数, 所以(a5bj)m≠1. 故此时群同态θ不存在. 若θ∈Hom(Q4m,G10pn), 则由xm=y2可得 (a5bi)m=(xθ)m=(xm)θ=(y2)θ=(yθ)2=(a5bj)2=1. 又因为m是奇数, 所以(a5bi)m≠1. 故此时群同态θ不存在. 由定理1中1)的情形②,④可知上述两种情形均成立. 由定理1中1)的情形⑥,⑧可知上述两种情形均成立. 必要性. 若θ∈Hom(Q4m,G10pn), 则由xy=yx-1可得 bj=xθyθ=(xy)θ=(yx-1)θ=yθ(xθ)-1=b-j, 即b2j=1, 因此j=0; 其次由xm=y2及已知条件可知j=0成立, 因此当θ为群同态时j=0. 充分性. 当j=0时,θ显然为平凡同态. 在此情形下群同态θ有1种选择. 任取xsyt∈Q4m, 其中0≤s<2m, 0≤t<2, 令(xsyt)θ=(bh)s(a5bj)t. 设xs1yt1,xs2yt2∈Q4m, 若xs1yt1=xs2yt2, 则xs1-s2=yt2-t1∈〈x〉∩〈y〉=1或y2=xm, 于是2m|(s1-s2)且4|(t2-t1)或2m|(s1-s2-m)且4|(t2-t1-2). 由引理2中1)可知(a5bj)t2-t1=1, 于是(a5bj)t1=(a5bj)t2. 又由已知条件可知(bh)s1=(bh)s2, 从而 (bh)s1(a5bj)t1=(bh)s2(a5bj)t2, 综上可知, 当p|m时, |Hom(Q4m,G10pn)|=1+pn+k. 下面分8种情形证明. 由定理1中2)的情形①,②,⑤,⑥可知上述4种情形均成立. 由定理1中1)的情形②,⑥可知上述两种情形均成立. 由定理3中1)的情形①,②可知上述两种情形均成立. 证明: 设θ∈Hom(Q4m,G10pn),yθ的选取方式同定理1. 1) 当p|m时,xθ的选取方式同定理2中1). 下面分6种情形证明. 由定理1中1)的情形②,⑥可知上述两种情形均成立. 由定理3中1)的情形①,②,⑦,⑧可知, 上述4种情形均成立. 综上可知, 当p|m时, |Hom(Q4m,G10pn)|=1+pn+k. 下面分4种情形证明. 由定理1中2)的情形①,②可知上述两种情形均成立. 由定理3中1)的情形①,②可知上述两种情形均成立. Asai和Yoshida猜想[3]: 设A,G是两个有限群,A′是A的换位子群, 则 |Hom(A,G)|≡0(mod(|A/A′|,|G|)) 成立. 下面验证群Q4m到群G10pn的同态个数满足Asai和Yoshida猜想. 推论1设m是正整数且m≥2,p是大于5的素数, 则 (3) 根据定理1~定理4易得式(3)成立, 即群Q4m到群G10pn的同态个数满足Asai和Yoshida猜想.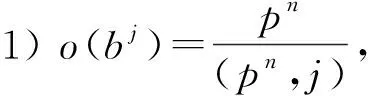
2 主要结果

































































3 应 用