初中数学思维可视化教学课例设计

石长虹

摘 要：可视化技术是一种计算与处理方法，能将抽象的数据和符号关系变成具体的、直观化的关系。在数学中引入可视化技术，将原本不可见的思维用图示的方式清晰地呈现出来，让学生能亲眼所见模拟和计算的过程，实现对信息的可视化、数据的可视化、计算的可视化和隐性思维的显性化，加快了学生对知识的获取和吸收，提高了课堂的教学效率。

关键词：数学思维;可视化;初中课堂;教学策略

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2020）06C-0067-02

恩格斯说：“一个民族想要站在科学的最高峰，就一刻也不能没有理论思维。”与知识学习相比，思维能力的发展并不是一个自然的过程，而是要经过专门的培养和训练，因此，素质教育背景下的教学改革强烈呼唤“思维教育”。数学是一门思维性和逻辑性极强的学科，数学教育的目的不仅是让学生掌握数学知识，更为重要的是发展学生的数学思维，让学生运用数学思维来分析问题和解决问题，为学生提供一种学习数学的新方法。

一、抽象思维可视化

数学抽象思维是以数学概念为思维材料，通过数学判断、推理的形成来反映数学本质，揭示数学知识之间的内在联系。抽象思维是对已获得的数学事实进行加工处理，从中抽离出数学本质特征的过程。抽象思维可视化，是利用图示的方式将数学概念、数学规律、概念与规律之间的因果关系、思维的逻辑及顺序表达出来。如果说数学概念是“点”，数学思维过程是“线”，那么，诸多的“点”与“线”结合起来，就形成了一个整体，从而表现出数学的本质。在抽象思维可视化的过程中，学生可根据自己的想法对其进行灵活改变，达到与自己思维相匹配的状态。

数学概念反映的是现实对象的数量关系和空间形式的本质特征，是学生进行数学推理和证明之本，扎实掌握数学概念，能提高运算技能和问题解决能力。实现思维可视化，有助于学生记忆并灵活运用。

以菱形概念教学为例。菱形是学生在学习平行四边形之后，要掌握的一种特殊的平行四边形。本节课教学重难点是菱形的性质及判定方法理解。由于菱形和矩形都属于特殊的平行四边形，所以它们都具有平行四边形的性质。在研究菱形时，教师可引导学生从平行四边形入手，对菱形和矩形所具有的特征进行判定，实现对原有知识的同化，强化对菱形知识的理解。为此，我们根据平行四边形与矩形、菱形的从属关系，采用可视化技术，利用表格将矩形的知识点研究策略和菱形进行对比，如下表所示。

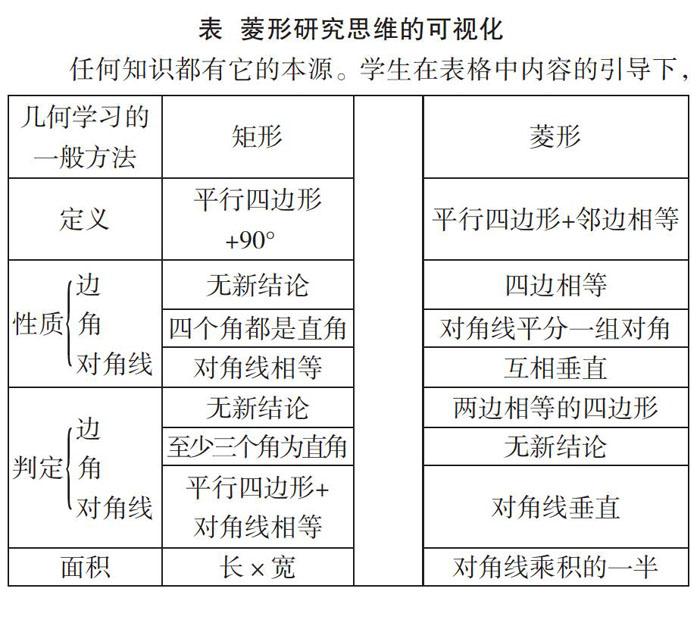
表  菱形研究思维的可视化

任何知识都有它的本源。学生在表格中内容的引导下，以小组为单位，进行自主探究，有利于培养学生的自主性。这样将菱形的性质及判定方法（三个方面：边、角和线）进行总结和类比，清晰直观、简单完整，不仅将菱形概念中最核心的内容简明扼要地表达出来了，而且通过上、下位知识的联系，能让知识体系更具有连贯性。此外，通过对比，可帮助学生将矩形的判断方法迁移到菱形的判定中，实现知识的迁移和运用。

二、形象思维可视化

数学形象思维是以数学表象为思维材料，以观察、猜想、比较、类比、联想的形式，对形象材料的意识加工而得到领悟的一种思维方式。通过教学实践发现，学生在学习过程中数学表象储备少，知识零散，且缺乏联想意识。造成这种现象的原因是学生形象思维能力的欠缺，及部分教师在教学中忽视了直观演示的作用，学生无法对知识点形成相对透彻的理解，难以构成一张清晰的数学知识网络。

形象思维可视化是将以语言描述的数学情景或以符号表达的数学公式，形象地转化为数学图形进行的思索。由于相比于抽象思维，想象思维更具有动态性和直观性，有利于学生理解和深化知识。

以二次函数y=ax2+bx+c（a≠0）性质教学为例。教师用几何画板演示，学生观察，当改变a的大小时，抛物线开口大小随之变化，当a的符号改变时，抛物线的开口方向随之改变。当a=0时，图象变为一条直线，不再是抛物线，所以二次函数a≠0。那么当b=0或c=0时，函数图象又有什么变化呢？一位学生在讲台上用几何画板进行演示，其余学生在观察的同时，验证自己的猜想。结果发现当b=0，抛物线关于y轴对称;当c=0时，抛物线经过原点;当b=0且c=0，抛物线经过原点且关于y轴对称。这样通过该阶段的动态演示，学生了解了二次函数的二次项系数不能为零，以及各个参数变化时抛物线大小、开口的变化情况。那么，y=ax2、y=a（x+m）2与y=a（x+m）2+k有什么区别和联系呢？

首先分析y=ax2和y=a（x+m）2，取m=2时，利用几何画板分别画出二次函数y1=ax2和y2=a（x+2）2的圖象，发现：两条抛物线开口相同、形状相同，只是位置不同。在y1=ax2上取一点P，再在y2=a（x+2）2上找到P点对应的Q，计算P和Q两点的坐标，接着让P点在y1上进行运动，带动Q点同时运动，学生通过观察发现，两点坐标无论如何变化，其横坐标差都是2，纵坐标相同。也就是y2=a（x+2）2图象可看作是y1=ax2向左平移2个单位得到的。类似的当取m=-2时， y2=a（x-2）2图象可看作是y1=ax2向右平移2个单位得到。

通过刚才的演示，学生已经掌握了图象性质的分析方法，于是让学生以小组为单位，自主的探究y=a（x+m）2和y=a（x+m）2+k、 y=ax2和y=a（x+m）2+k的区别和联系。利用几何画板，让学生直观观察到二次函数图象的动态变化过程，获得生动的数学形象，简洁明了、一目了然，学生的数学形象思维能力得到了有效的训练。

三、直觉思维可视化

伟大数学家彭加勒曾说：“逻辑用于证明，直觉用于发明。”数学直觉思维是以数学概念和数学表面结合而成，以丰富的经验和知识的结构为依据，对思维对象从整体上进行考查，不借助于数学逻辑推理而仅凭感知、想象去作出猜想和判断，它是一种思路简单化的思维方式，以高度简练的方式洞察事物的本质，省去了一步一步分析推理的中间环节。将直觉思维可视化，是在脑海中经过抽象思维后有了数学模型，又经过形象思维形成数学模型的过程。学生在看到另一个数学题目后，能迅速地联想到这个数学模型并灵活运用进行解题，从而实现知识的有效迁移。

以平面内n条直线最多能把平面分成几个部分教学为例。

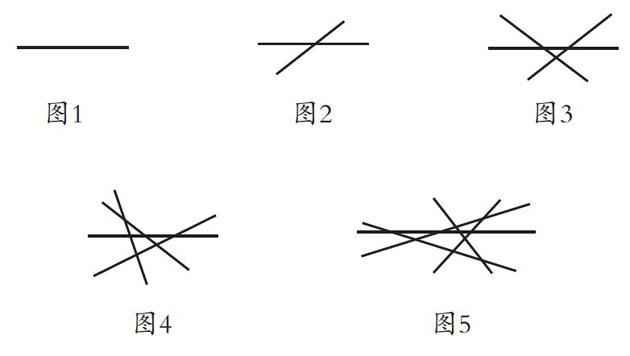
分析：这道题目乍一看非常抽象，大部分学生感觉没有头绪。但仔细分析题目后，就会发现与我们曾经学习过的问题比较像。从1条直线开始，如图1所示，平面被分成2个部分;图2中，2条直线，相交于1个交点，将平面分为4个部分;图3中，3条直线，相交于3个交点，平面分为7个部分;图4中，4条直线，相交于6个交点，将平面分为11个部分;图5中，5条直线，相交于10个交点，将平面分为16个部分。这样问题就变得很显性化了。

我们结合图形开始寻找规律，从图1到图2，发现直线的交点多1个，平面就会被多分成2个部分，即交点数从1→2，平面被分成2→2+2部分;从图2到图3，交点数从2→3，平面被分成（2+2）→（2+2）+3部分。以此类推，结果发现，平面中直线相交每增加k个交点，平面就会被多分成（k+1）个部分。所以，平面内n条直线最多可以将平面分为： 2+2+3+4+5+…+n=2+2+3+4+5+…n=1n（n+1）/2+个部分。

可见，在数学习题训练时，教师的责任并不仅向学生讲解题的步骤和答案，更为重要的是将数学题目中的基本模型给学生讲清楚，使其能深深根植于学生的脑海中，这样，当学生再次遇到类似的题目就能迅速地想到对应的数学模型，当学生所积累的数学模型越来越多，在进行数学解题时，就越容易作出直觉判断。所以，从某种意义上来说，直觉思维的可视化是抽象思维和形象思维可视化融合后产生的飞跃。

四、結束语

总之，初中数学知识点繁多且灵活性较强，借助思维导图、表格、流程图等技术实现思维可视化，可以让学生更加轻松直观记忆，理解各知识点间的内在联系，不仅有利于锻炼学生的迁移能力和思维拓展能力，也为学生将来解决问题提供了有效的解决方法，促使学生的逻辑思维发展更为完善。

参考文献：

[1]陈玲.初中数学教学中如何培养学生的数学思维能力分析[J].数学学习与研究（教研版），2019，（15）.

[2]堵薇薇.基于思维品质培养的几何概念课的教学设计与实践——以“锐角三角比的意义”一课为例[J].上海中学数学， 2019，（4）.

[3]陈梅.数学思维能力在初中数学教学中的培养策略分析[J].数学学习与研究（教研版），2019，（9）.

[4]潘朝夕.“思维可视化”在初中数学教学上的应用[J].兴义民族师范学院学报，2015，（2）.

[5]马万山.思维导图在初中数学课堂教学中的研究[J].教育观察，2019，（42）.