超声辅助磨削杯形砂轮变幅器设计与试验*

牛金荣 秦慧斌 冯 毅 周瑞峰 吕 明

(1 中北大学先进制造技术山西省重点实验室 太原 030051)

(2 太原理工大学精密加工山西省重点实验室 太原 030024)

0 引言

当前，硬质合金、陶瓷、光学玻璃、金属基碳化硅复合材料等硬脆材料已广泛应用于航空航天、医疗器械、汽车制造等诸多领域[1]。此类材料具有优异的机械、物理和化学性能，如密度低、比模量大、硬度高、化学稳定性高、耐磨损、耐高温、耐腐蚀等，应用前景非常广阔[2]。但硬脆材料具有高脆性、低断裂韧性的特点，弹性极限与强度非常接近，加工过程中，当材料所受的载荷超过弹性极限时，就会产生断裂破坏，在加工表面上出现裂纹及凹坑，表面质量和性能受到严重的影响[3]。在使用传统方法加工的过程中，存在着刀具磨损严重、切削力大、加工效率低、加工表面质量差、容易造成材料损伤等诸多问题，不利于硬脆材料的推广使用。

超声磨削具有降低磨削力和磨削热、减小加工损伤、提高加工效率和精度、延长刀具寿命等优点，是一种对复合材料、硬脆性材料等难加工材料有效的精加工工艺[4]。超声磨削系统是实现超声磨削的核心执行装置，在国内外现阶段研究中，从运动方式上可将其分为工件旋转型和刀具旋转型；从供电方式上可分为接触供电式和非接触供电式；从装置结构上可分为主轴附件式和平台式。其中主轴附件式的磨削装置应用前景较为广泛。该装置能够方便地安装在传统机床上使用，利用普通机床实现超声磨削加工，对机床的改动很小，不影响机床原有的使用，具有良好的市场应用价值。

在超声磨削系统中，激励砂轮产生超声频率振动的关键部件是由变幅杆与砂轮组成的变幅器。砂轮规格种类繁多，结构形状多样，如何正确设计变幅器，便成为了超声磨削系统设计的首要环节。杯形砂轮在磨削加工中应用广泛，常用来端磨平面及刃磨刀具。在关于杯形砂轮磨削加工的研究中，Wu等[5]通过分析杯形砂轮对陶瓷涂层进行平面磨削的过程，建立了杯形砂轮的磨削力理论模型并进行了实验验证。王少雷等[6]则研究了杯形砂轮磨削过程中磨削深度和磨削速度对加工质量的影响。将杯形砂轮与超声振动相结合，以杯形砂轮为磨削工具头的超声磨削系统可利用杯形砂轮实现对平面的超声磨削加工。图1为以杯形砂轮为加工工具的超声辅助磨削主轴附件式工具系统结构简图。该装置通过外套筒上的标准刀柄与机床主轴连接，通过导电滑环完成超声波发生器与换能器间的电能传输。杯形砂轮在主轴带动下做旋转运动的同时，在换能器的激励下产生超声振动，完成对工件的超声辅助磨削。在该超声磨削系统中，杯形砂轮变幅器的正确设计具有重要意义。

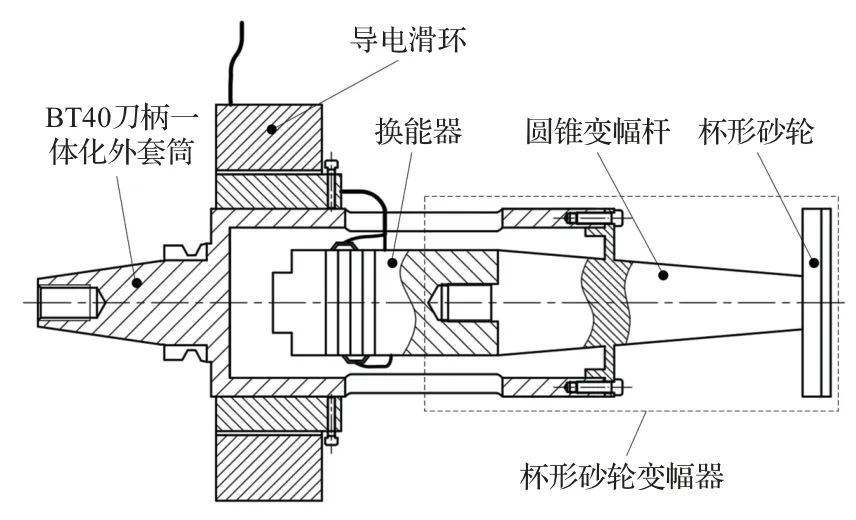
图1 杯形砂轮超声辅助磨削主轴附件式工具系统Fig.1 Spindle accessory UAG device with a cup wheel

在具有杯形结构的变幅器研究中，一种设计方法是完全通过有限元软件进行设计，其中Brecher等[7]基于有限元软件和Matlab 提出了一种应用于超声辅助磨削的杯形砂轮变幅器的快速设计方法。同样基于有限元软件，唐岳[8]设计了用于瓷砖磨削加工的杯形砂轮变幅器。与以上两者不同，另一种方法是通过理论对变幅器进行设计，并结合有限元进行修正。Xu[9]基于等效电路法和有限元分析，研制了具有锥形深孔的杯形工具变幅器。陈汇资等[10]基于一维纵振理论、薄板弯曲振动理论和耦合振动理论，结合有限元分析对一种用于硬脆材料高精度曲面加工的杯形工具变幅器进行了全谐振设计，并通过有限元软件对杯结构的不同尺寸对变幅器整体谐振频率的影响进行了研究。赵金坠[11]则基于复合变幅杆振动理论、薄盘弯曲振动理论、耦合振动理论，设计了一种忽略杯形砂轮磨料层的杯形工具变幅器。马付建等[12]基于细长杆纵振理论和薄圆盘振动理论，结合有限元分析，对杯形工具变幅器进行了非谐振一体化设计。在上述基于振动理论对变幅器进行设计的研究中，均采用薄盘弯曲振动理论来建立杯形工具变幅器中圆盘段的理论模型，该理论假设条件中要求圆盘厚度与直径的比值非常小，而杯形砂轮金属基体的圆盘部分厚度与直径的比值较大，更加适合用中厚盘理论来进行计算。

针对上述问题，本文对超声辅助磨削主轴附件式工具系统中杯形砂轮变幅器进行了研究，将杯形砂轮变幅器划分为圆锥杆、圆盘、圆管和磨料层4部分，通过Mindlin 中厚盘理论得出了圆盘的横向位移、径向转角、径向弯矩和径向剪力的函数表达式，并分别建立了圆锥杆、圆管和磨料层的位移和应变函数表达式。通过变幅器各组成部分之间的边界条件和耦合条件，推导了杯形砂轮变幅器的频率方程。在理论基础上，通过Matlab开发了杯形砂轮变幅器设计软件。利用该设计软件对变幅器进行了设计，并通过有限元软件进行分析及修正，最终确定了杯形砂轮变幅器的尺寸并制作了实物。将研制的杯形砂轮变幅器与BT40 一体化外套筒、导电滑环装配在一起，组成了杯形砂轮超声辅助磨削主轴附件式工具系统并进行了试验分析。

1 杯形砂轮变幅器设计理论

1.1 变幅器理论模型

杯形砂轮变幅器由杯形砂轮、圆锥杆和紧固螺母组成，杯形砂轮通过螺纹连接固定在圆锥杆小端。杯形砂轮包括金属基体和磨料层两部分，为便于分析，将金属基体假想为由圆盘、圆管组成的结构。图2为杯形砂轮变幅器的结构示意图，其中I为圆锥杆，II为砂轮金属基体圆盘，III为砂轮金属基体圆管，IV为砂轮磨料层，V为六角螺母。由于螺母体积较小，因此在理论分析中将其忽略。圆锥杆左端半径为R1，右端半径为R2，长度为L；砂轮金属基体圆盘的中心孔半径为R3，盘厚为t1；砂轮金属基体圆管的内圆半径为R4，外圆半径为R5，管长为t2；砂轮磨料层的厚度为t3。变幅器各部分的密度、弹性模量和泊松比分别用ρi、Ei、μi(i=1,2,3)来表示，i=1,2,3 分别对应圆锥杆、杯形砂轮金属基体、杯形砂轮磨料层。

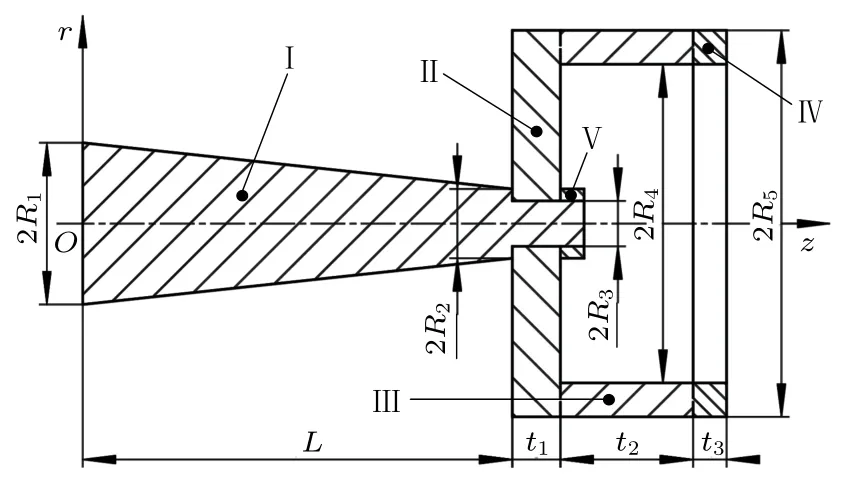
图2 杯形砂轮变幅器结构Fig.2 Structure of cup wheel transformer

杯形砂轮变幅器中，圆锥杆左端连接压电换能器，换能器激励圆锥变幅杆作纵向振动，变幅杆激励圆盘做横向弯曲振动，在圆盘外侧的圆管和磨料层则在圆盘边缘的带动下做纵向振动，在磨料层的右端，振动以纵向振动的形式输出。

(1)圆锥杆

变幅器工作时，圆锥杆在换能器激励下产生纵向振动，其纵振位移ξ1和应变ε1的函数表达式为[13]

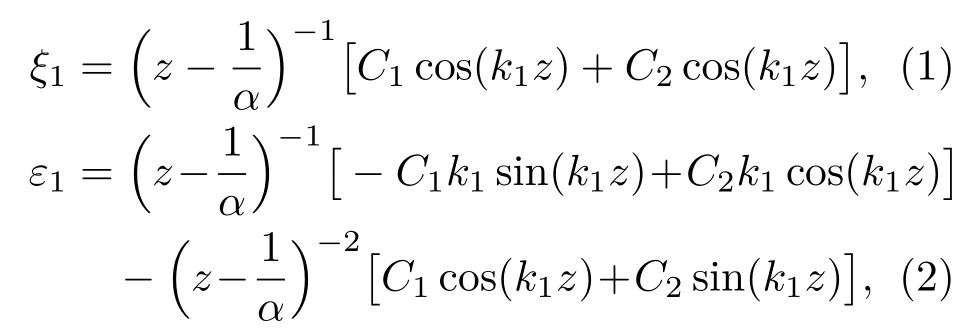
(2)圆盘

圆盘在锥形变幅杆纵向振动的激励下做横向弯曲振动。依据Mindlin中厚盘求解理论，圆盘的横向位移w和径向转角βr的函数表达式为[14]

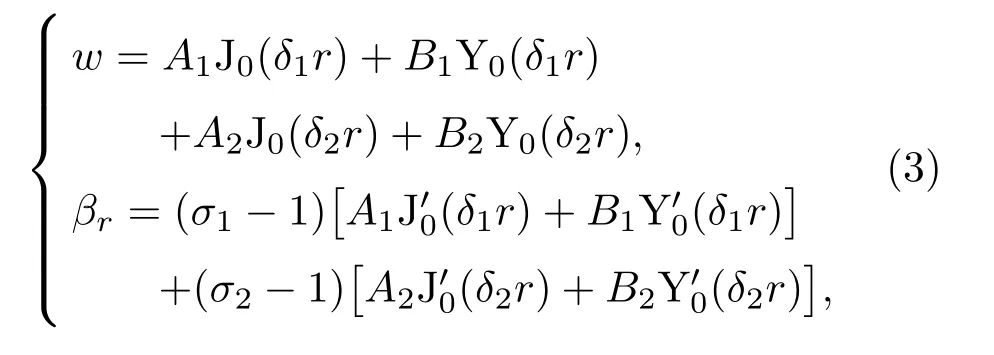
其中，

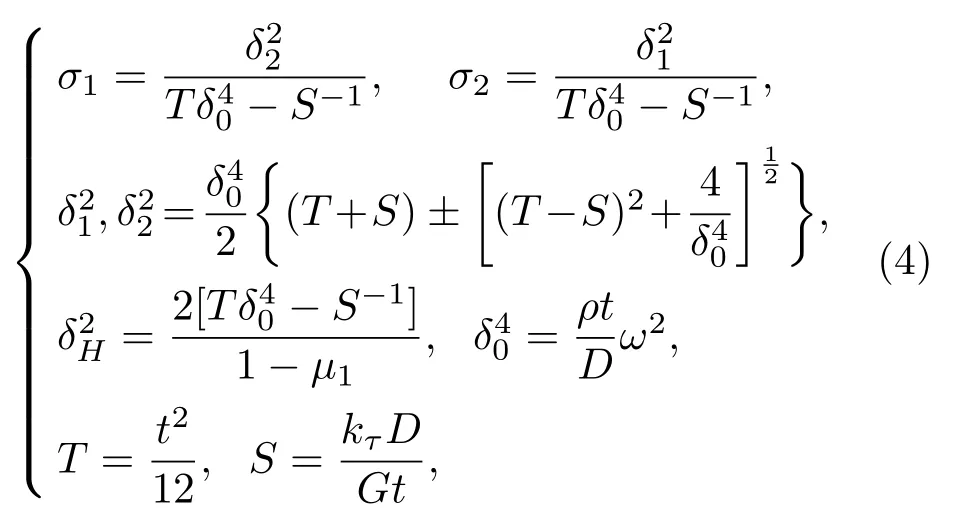
其中，Aj、Bj(j=1,2)为待定常数，由圆盘边界条件确定；J0(·)、Y0(·)分别为圆盘横向弯曲振动时的节径数为零的第一类和第二类贝塞尔函数。

此外，根据Mindlin 理论，圆盘径向弯矩Mr和径向剪力Qr为

式(5)中，弯曲刚度D、剪切弹性模量G、剪切影响因子kτ的计算方式为

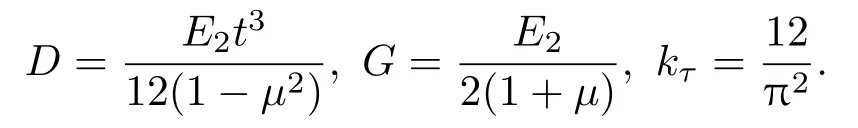
(3)圆管

当杯形砂轮变幅器圆管部分的直径超过四分之一波长时，其实际振动表现为纵向、径向耦合振动，求解该振型的理论非常复杂，难以得到解析解。为了简化分析，忽略了其径向振动，采用了一维纵振理论来建立圆管部分的理论模型[15]。在这种情况下，圆管纵振位移ξ3和应变ε3的函数表达式为

其中，A3、B3为由圆管边界条件确定的待定常数。圆波数k3、圆频率ω、纵波波速c3的计算方式为。

(4)磨料层

磨料层形状近似圆管状，因此也用忽略径向振动的一维纵振理论进行简化计算。磨料层纵振位移ξ4和其应变ε4的函数表达式为

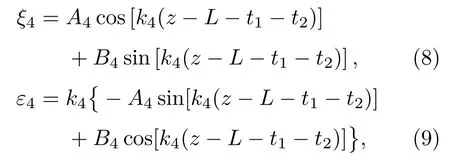
其中，A4、B4为由磨料层边界条件确定的待定常数。圆波数k4、圆频率ω、纵波波速c4的计算方式为。

1.2 频率方程

圆锥杆的大端面和换能器的输出面通过螺纹紧固连接，但换能器处于悬空状态，圆锥大端无限制其位移的固定约束，为自由端，因此大端面上应力为零，即E1ε1|z=0=0，将式(2)代入得

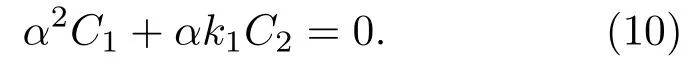
圆锥杆z=L、r=R2处与圆盘r=R3处通过螺母紧固连接，该接触面上满足受力相等和位移相等的连续条件，即

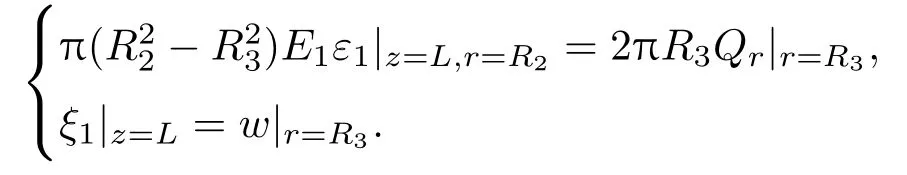
将式(1)～(5)代入得

杯形砂轮通过螺母紧固在圆锥杆小端后，其连接可近似视为刚性连接，圆盘无径向转动，故其在r=R3处的径向转角βr为零，即βr|r=R3=0，将式(3)代入得

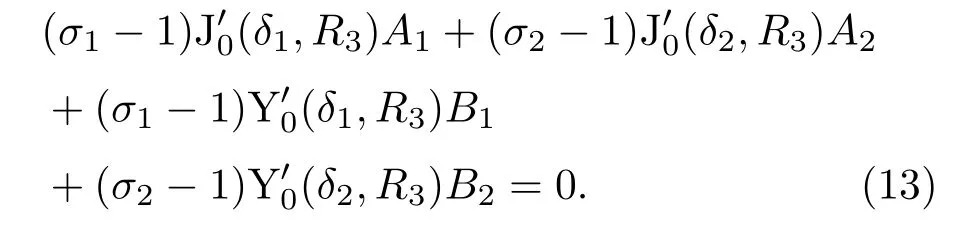
当杯形砂轮变幅器工作时，圆盘在圆锥杆纵向振动激励下做横向弯曲振动，无径向转动，故其r=R5处的径向转角βr为零，即βr|r=R5=0，将式(3)代入得

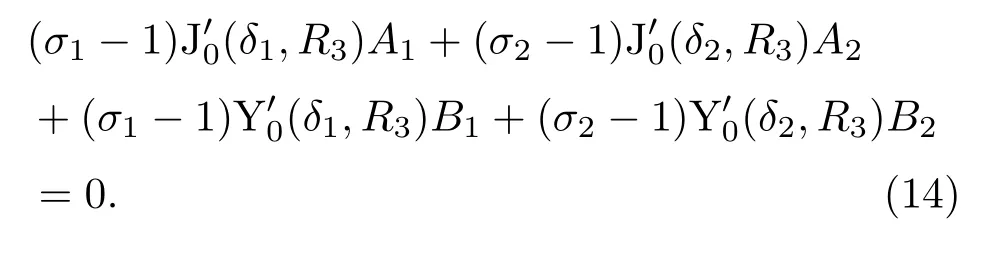
圆盘和圆管同属杯形砂轮的金属基体，故在两者间假想的接合面处满足受力相等和位移相等的连续条件，即

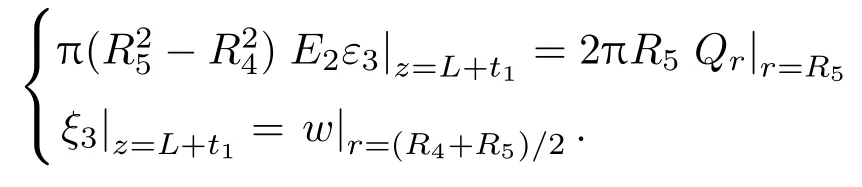
将式(3)～(7)代入得

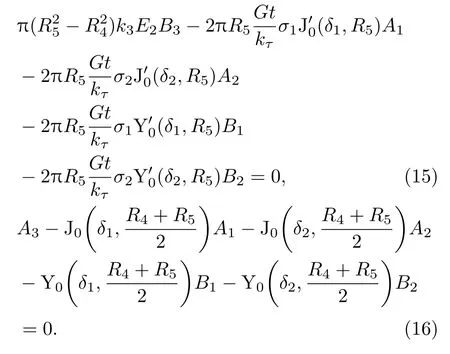
杯形砂轮中，磨料通过结合剂固结在金属基体上，因此圆管和磨料层的在连接面处满足受力相等和位移相等的连续条件，即

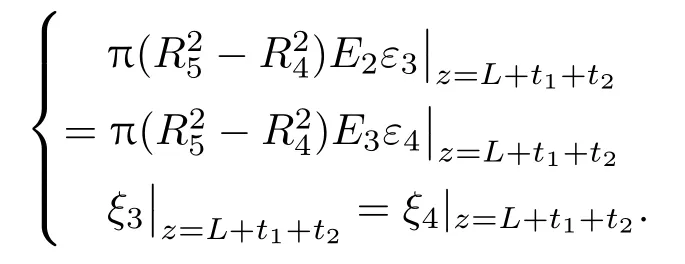
将式(6)～(9)代入得

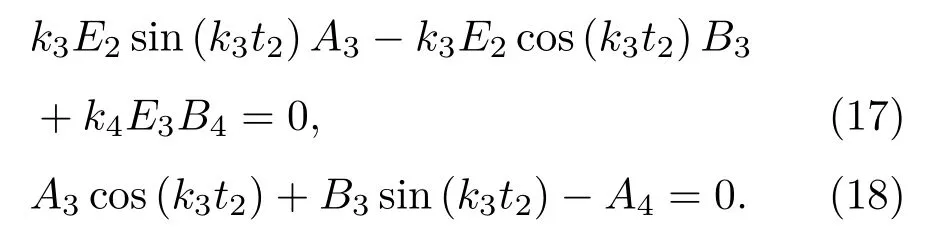
磨削加工中，杯形砂轮磨料层表面与工件相接触并受到磨削力的作用。然而，加工过程中的磨削力是动态变化的，现阶段难以对其进行建模及计算。为方便计算，将磨料层的右端简化为自由端，受力为零，即E3ε4|z=L+t1+t2=0，将式(9)代入得

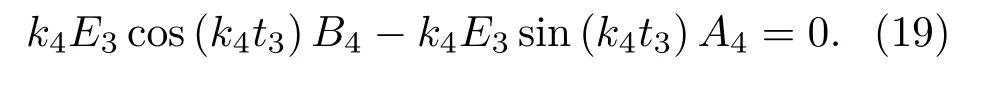
联立式(10)～(19)，经过整理可以得到一个齐次方程组：

其中，

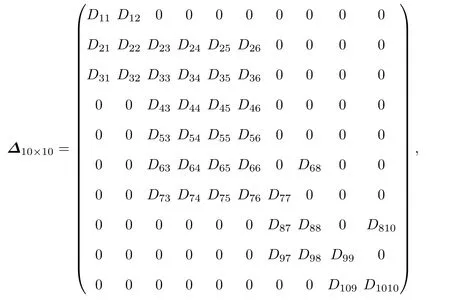
ζ10×1=[C1C2A1A2B1B2A3B3A4B4]T.

Dpq(p,q=1,2,···,10)为式(10)～(19)中的待定常数Ai、Bi、Cj(i=1,2,3,4；j=1,2)的系数，可由变幅器各部分几何尺寸、材料性能参数和工作频率求得。列向量ζ10×1中的元素全部为零时，变幅器处于静止不振动的状态，与实际情况不符。因此，列向量ζ10×1应取非零解，其充要条件为

式(21)即为杯形砂轮变幅器的频率方程。若变幅器有一个尺寸未知，则根据变幅器的已知几何尺寸、材料性能参数和设计频率，可由频率方程求得该未知尺寸，完成变幅器的设计。

2 杯形砂轮变幅器设计

2.1 变幅器设计软件

为简化设计流程，基于上述理论利用Matlab开发了杯形砂轮变幅器设计软件，如图3所示。

软件流程图如图4所示。首先在界面中输入杯形砂轮变幅器的材料性能参数、尺寸参数、谐振频率，并选择默认求解区间或自定义求解区间。然后单击“计算”键，程序将输入参数代入至求解函数中进行计算。若有解，则将结果显示在“变幅杆长度求解结果”一栏中，同时给出对应的求解曲线图；若无解，则提示求解无效，需调整参数重新计算。

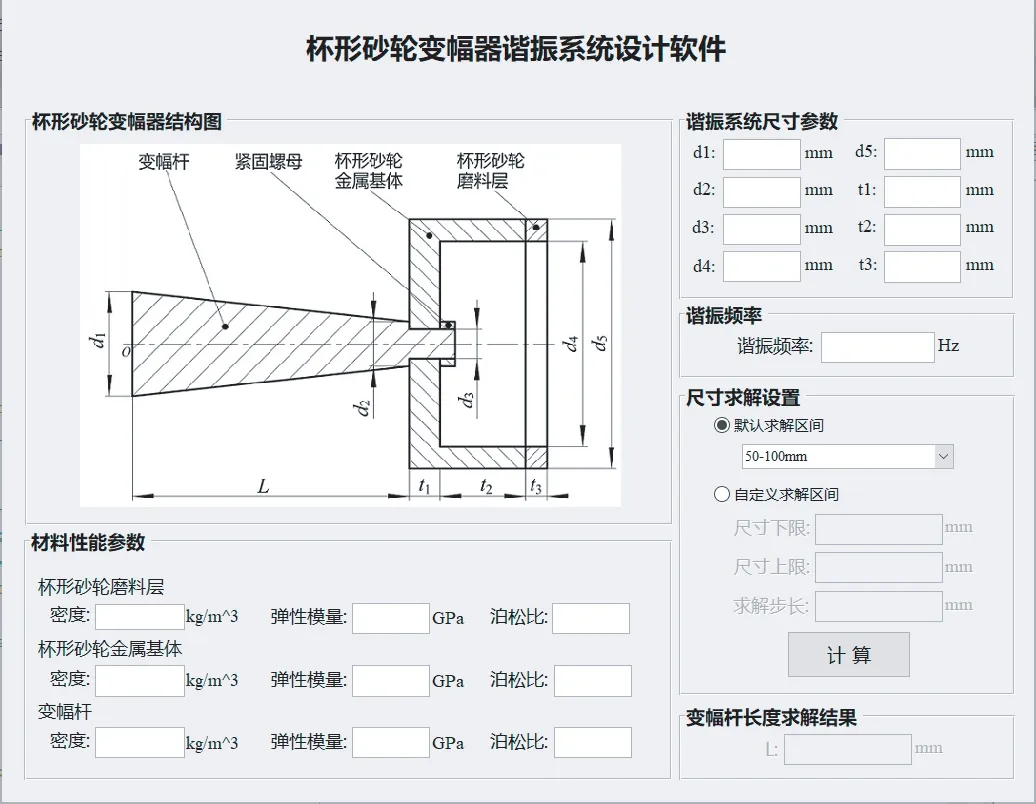
图3 软件人机交互界面Fig.3 Human-computer interface of the software

图4 软件流程图Fig.4 Folwchart of the software

2.2 变幅器设计

利用上述软件对杯形砂轮变幅器进行设计，频率为20 kHz，圆锥变幅杆材料为45#钢，杯形砂轮金属基体材料为铝，磨料层材料为金刚石。各材料的性能参数如表1所示。将圆锥变幅杆杆长L作为待求尺寸，圆锥杆其余尺寸及砂轮尺寸等已知尺寸如表2所示。将上述参数输入至变幅器设计软件中求解，得圆锥变幅杆杆长L为137.1 mm。

表1 材料性能参数Table 1 Mechanical properties of materials

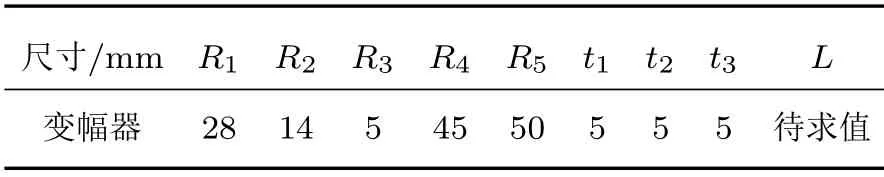
表2 杯形砂轮变幅器尺寸Table 2 Parameters of cup wheel transformer

3 变幅器有限元分析及修正

根据理论设计所得的变幅器尺寸，建立了变幅器的三维模型并对其进行了模态分析。其结果如图5(a)所示，此时变幅器的谐振频率为18.824 kHz，比预期的设计频率20 kHz 小1176 Hz，误差为5.56%，需对变幅器进行进一步修正。造成理论计算与有限元模态分析之间存在误差的原因有：(1)当杯形砂轮变幅器圆管部分的直径超过四分之一波长时，其实际振动表现为纵向、径向耦合振动，求解该振型的理论非常复杂，难以得到解析解。为了简化分析，忽略了其径向振动，采用了一维纵振理论来建立圆管部分的理论模型，因而会导致一定的误差。(2)频率方程是基于理想状态下的圆锥杆纵向振动、圆盘横向弯曲振动、圆管一维纵向振动的理论公式推导而得，与仿真过程中模拟实际所设置的条件并不完全一致，因而会造成一定的误差。(3)由于小端螺纹、紧固螺母等部分体积较小，在建立变幅器理论模型时将其忽略不计，而在ANSYS模态分析中为了更加接近实际情况，添加了这些结构，因而会导致一定的误差。

修正时，将圆锥变幅杆杆长缩短至128 mm，其余尺寸均保持不变。建立修正后的三维模型并导入ANSYS 中进行模态分析，其结果如图5(b)所示。此时变幅器的谐振频率为19.942 kHz，与设计频率20 kHz 相差58 Hz，误差为0.29%，满足设计要求。至此，变幅器主要尺寸已设计完成。

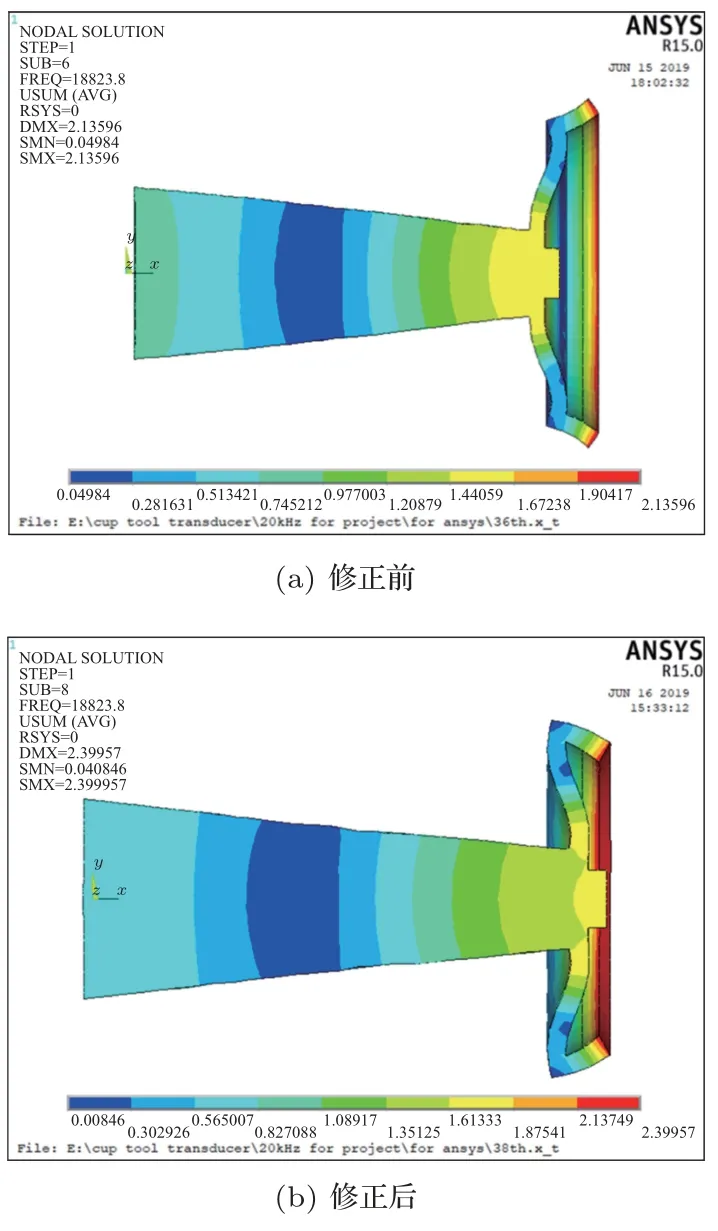
图5 变幅器模态分析结果Fig.5 Modal analysis results of the transformer

变幅器主要尺寸设计完成后，需在圆锥杆上添加法兰盘，用以连接超声辅助磨削装置的BT40 刀柄一体化外套筒。为避免将超声振动传递到套筒上引起能量耗散，降低系统稳定性，法兰盘的位置应设在圆锥杆的节点上，使其保持静止不振动的状态。但是，变幅杆轴线上的节点和外表面的节点存在位置偏差，针对法兰盘设置在哪个节点上更为准确这一问题，许多学者进行了研究。赵明利等[16]借助有限元软件对变幅杆节点进行分析研究，结果表明带工具头变幅杆外廓线与轴线上节点位置不重合，按轴线节点位置安装的法兰存在较大的振动位移。陈俊波[17]研究了圆柱形阶梯变幅杆的法兰最佳位置，发现应在变幅杆外圆面位移为零的节点添加法兰，而非轴线上位移为零的节点。赵波等[18]发现轴线上位移为零的节点位置所对应的外廓线处位移并不为零，通过Matlab 得出轴线到外轮廓之间所有零节点的位置并不在同一个平面上，而是形成一个曲面。以上研究表明，在变幅杆上设置法兰盘时，其位置应选择在变幅杆外表面的节点上，而非轴线的节点上。将所设计的变幅器的三维模型导入ANSYS 中进行谐响应分析，在圆锥杆大端端面施加6 μm 的轴向位移载荷，频率设置为19.942 kHz，定义路径设置在圆锥杆外表面的母线上，通过谐响应分析得到圆锥杆母线上的纵振振幅分布如图6所示。

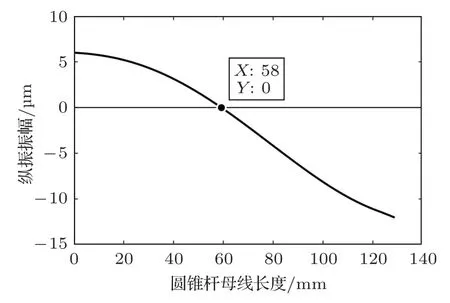
图6 圆锥杆母线方向振幅分布Fig.6 Displacement distribution of the conical horn along the generatrix

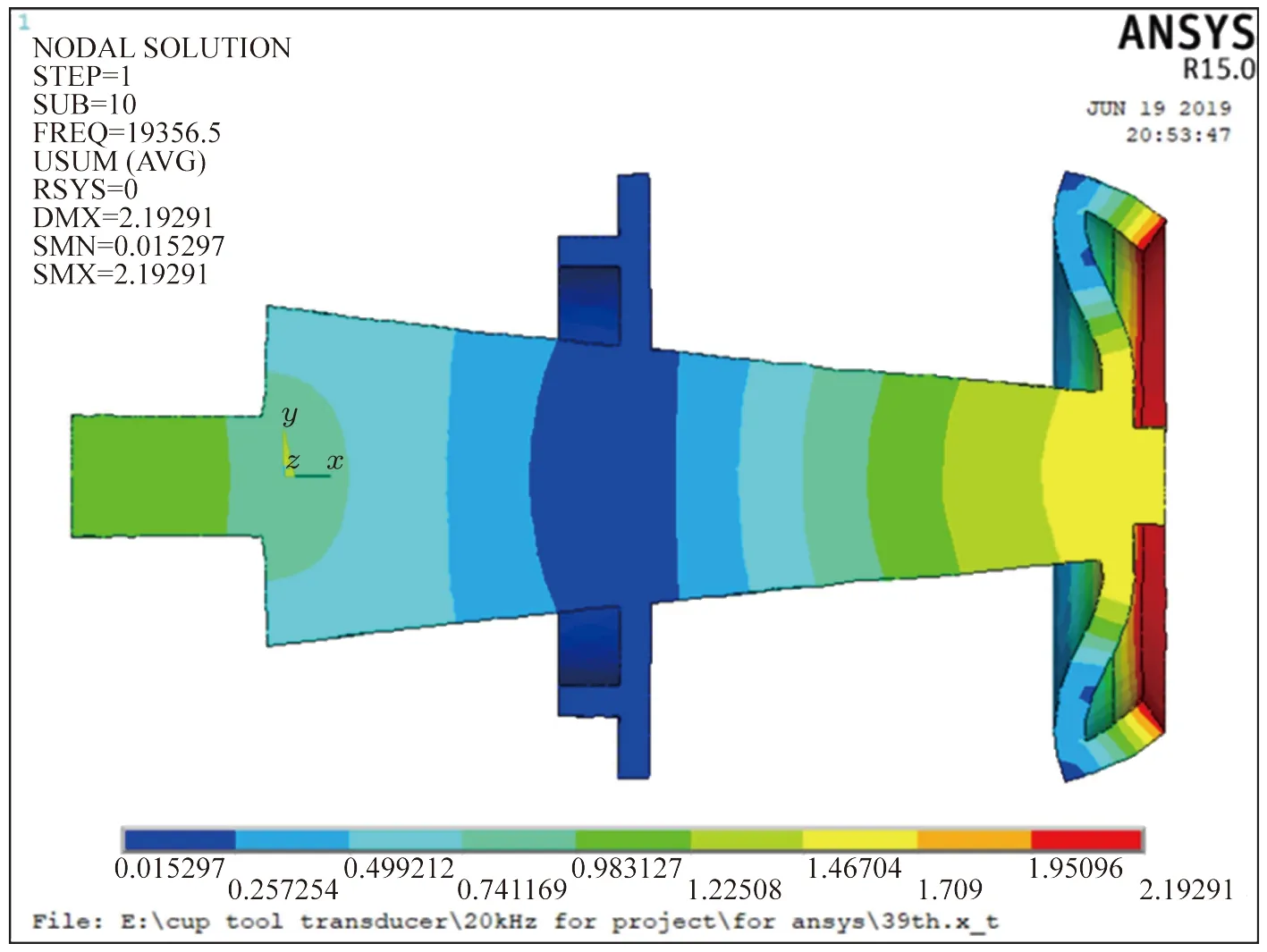
图7 杯形砂轮变幅器模态分析结果Fig.7 Modal analysis result of the cup wheel transformer

圆锥杆的节点位于沿母线方向距大端58 mm处，应在此处添加法兰盘。在Solidworks中建立添加了法兰盘及连接螺栓的三维模型并导入到ANSYS中进行模态分析，其结果如图7所示。所添加的法兰完全处在节点位置，不发生振动。变幅器在添加了法兰及圆锥杆大端的连接螺栓后，模态分析所得的谐振频率有所降低，由19.942 kHz 变为19.357 kHz，与设计频率20 kHz相差643 Hz，误差为3.2%，在所允许的误差范围内。在模态分析得到的全部模态结果中，所需频率19.357 kHz 的上下相邻两阶频率分别为18.797 kHz 和20.333 kHz，分别相差560 Hz和976 Hz，不会对该频率造成干扰。

4 试验分析

依据上述尺寸设计结果加工了变幅杆，并购置了20 kHz 换能器及金刚石杯形砂轮。将三者与BT40 刀柄一体化外套筒和导电滑环装配在一起(在换能器、变幅杆、杯形砂轮的连接面处涂一层凡士林，减少能量损失)，组成如图8所示的杯形砂轮超声辅助磨削主轴附件式工具系统。该超声振动系统的电能传输由导电滑环完成，所使用的滑环最高转速为3000 r/min，工作寿命为2 亿转。工作时，超声波发生器产生的高频电能通过导线流入滑环转子，继而从滑环定子通过导线流入压电换能器，产生超声振动。

图8 杯形砂轮超声辅助磨削主轴附件式工具系统Fig.8 Spindle accessory UAG device with cup wheel

4.1 阻抗特性试验

为分析该超声振动系统的阻抗特性，使用PV70A型阻抗分析仪进行了阻抗分析试验，测试装置如图9所示，测得结果如图10所示。

图9 阻抗分析试验Fig.9 Impedance analysis test

阻抗分析结果表明，该超声振动系统的导纳曲线(粉色线)为一个完整的单圆，对数坐标图中红色线只有一对极小值和极大值，蓝色线呈现明显的“几”字形，说明该超声振动系统内部结构合理，压电陶瓷换能器和杯形砂轮变幅器阻抗匹配效果较好。在图10的参数栏中，该超声振动系统的谐振频率Fs为20.2344 kHz，与换能器实测频率19.9096 kHz 相比(利用阻抗分析仪对试验所使用的20 kHz 换能器进行测试，实际测得的谐振频率Fs为19.9096 kHz)，两者相差324.8 Hz，误差为1.63%。这说明该超声振动系统的工作频率与换能器本身的工作频率相差很小，当该超声振动系统处于谐振点时，换能器将处在一个较为理想的工作状态。此外，该超声振动系统反谐振频率Fp为20.5021 kHz，频率带宽Δf(Fp-Fs)为267.7 Hz，动态电阻R1为47.3 Ω，机械品质因素Qm为522.652，说明该超声振动系统振动效率较高。

图10 杯形砂轮超声辅助磨削系统阻抗测试结果Fig.10 Result of impedance analysis test

4.2 超声谐振试验

为研究该超声振动系统的谐振特性，进行了超声谐振实验，如图11所示。将超声波发生器与滑环转子间的导线相连接，启动电源，按下声波运行按钮，通过调频螺母调节超声波发生器输出的电信号频率，使超声振动系统处于谐振状态并保持稳定，此时，超声波发生器显示频率为20.151 kHz(通过调节调频螺母，该频率的值可在小范围内变化)。在砂轮表面均匀撒上碳化硅颗粒(砂轮以下部件用白色塑料纸包裹，以免碳化硅颗粒落入其中)，开启超声波发生器后，碳化硅颗粒在砂轮振动的作用下迅速聚集为两个圆环，如图12所示，表明砂轮底部呈现出节圆型弯曲振动，与理论设计中的弯曲振动假设和仿真模态结果相符。超声谐振试验证明所研制的杯形砂轮超声辅助磨削主轴附件式工具系统谐振效果较好，为进行超声加工实验奠定了基础。

图11 超声谐振试验Fig.11 Ultrasonic resonance test

图12 超声谐振试验结果Fig.12 Result of ultrasonic resonance test

5 结论

(1)推导了杯形砂轮变幅器的频率方程，建立了杯形砂轮变幅器设计理论，开发了杯形砂轮变幅器设计软件。利用该软件设计了20 kHz 杯形砂轮变幅器，并对其进行了模态分析，理论与仿真两者间的误差为5.56%。造成该误差的主要原因是，圆管部分的一维纵振理论模型无法完全准确地描述圆管实际的纵径耦合振动模态，因而导致设计结果存在一定误差。但该误差小于10%，仍满足工程应用的要求。

(2)在理论设计的基础上，利用有限元软件对所设计的变幅器进行了分析及修正，确定了杯形砂轮变幅器的最终尺寸。根据该尺寸加工了杯形砂轮变幅器实物，将其与刀柄一体化外套筒、导电滑环一起组装成了杯形砂轮超声辅助磨削主轴附件式工具系统。

(3)对所研制的杯形砂轮超声辅助磨削主轴附件式工具系统进行了阻抗分析试验和超声谐振试验。结果表明：该超声振动系统内部结构合理，压电陶瓷换能器和杯形砂轮变幅器阻抗匹配效果较好，能够实现稳定的超声振动，为进行超声磨削实验奠定了基础，为主轴附件式超声磨削装置的设计提供了理论参考。

(4)所研制的杯形砂轮超声辅助磨削主轴附件式工具系统在经过后续的动平衡调整合格后，即可对杯形砂轮的振幅进行测量，并进行超声磨削加工实验，对该超声磨削装置的性能(振幅、频率、发热、切削力、刀具寿命等)及工件加工质量(粗糙度、加工纹理、表面损伤等)进行研究。