时域有限差分法的混凝土超声波损伤分析*

刘昌明 陈亚琦 王志刚

(1 武汉科技大学 冶金装备及其控制教育部重点实验室 武汉 430081)

(2 武汉科技大学 机械传动与制造工程湖北省重点实验室 武汉 430081)

0 引言

混凝土质量的好坏直接影响到建筑物的安全性，工程中混凝土的质量检测常要求试件在不发生破坏的情况下进行，即无损检测。常用的无损检测方法有地质雷达法[1]、超声波法[2-3]和冲击回波法[4-5]等。地质雷达法采用电磁波检测，但混凝土中的钢筋对电磁场的影响较大，冲击回波法存在效率不高的问题，因此选用检测参数多、设备较为低廉、穿透能力强的超声波法进行缺陷检测是一种较好的选择。

目前在超声缺陷检测研究方面，国内外许多学者做了相关研究工作，取得了良好的效果。李志强等[6]从波幅、主频、波形的角度出发，介绍了混凝土超声波无损检测的原理和方法，检测混凝土的质量。蒋志峰[7]从频域的角度对碳纤维复合材料孔隙率进行分析并进行了缺陷诊断。杨慧敏等[8]提出用超声波能量衰减和频率成分的改变来表征木材缺陷的信息，并在此基础上用频谱分析了超声波信号。聂颖[9]、王凡[10]使用超声信号对工件进行故障诊断，通过时频分析进行缺陷判别。艾春安等[11]对粘接结构的声-超声接收信号，提出采用短时傅里叶变换的方法对缺陷进行识别，文章利用时-频方法对孔洞缺陷进行研究，但无法定量确定缺陷尺寸大小与信号参数之间的关系。孙志国等[12]运用超声波探伤仪对电熔池壁砖缩孔进行了检测，通过分析声时、振幅等检测信息来判断缩孔形状、尺寸和位置。孙志国等[13]还对烧结耐火材料进行超声检测，采用以判断声速为主的综合判断方法对烧结耐火砖的缺陷情况和内部结构特点进行检测。

为了研究混凝土内部缺陷体尺寸大小与接收信号之间的关系，需要对信号特征参量进行更加全面的分析。朱自强等[14]采用超声检测混凝土桥梁预应力管道的注浆质量，对采集到的信号从振幅、频率、相位等方面进行异常特征分析，对缺陷体的位置和形态进行准确的判断，但在缺陷定量解释方面与实际情况存在一定差异。李勇峰[15]运用时域幅值、时域能量、频域能量来研究耐火砖的密实度与缺陷情况，取得了较好的成果。基于超声波信号良好的穿透性与时频可控性，本文采用超声波主动激发作用于混凝土表面的方式，对检测信号的时域、频域展开分析，判断混凝土内部缺陷对超声波信号的影响并建立二者之间的联系。

1 超声波在混凝土内部传播数学模型

混凝土作为一种非均匀黏-弹性介质，其内部存在沙石、开裂缺陷体、水泥等多种声阻物质，需要建立一种声波在混凝土介质内部传播的运动学、动力学声场数学模型，求解出超声波声场与混凝土缺陷介质之间的数值关系。常用的数值模拟方法有有限元法、有限差分法、边界元法、有限积分法。其中有限差分法利用Taylor 展开式来近似代替波动方程中的微分，使微分形式的波动方程变成差分形式，其差分形式包含介质参量，能够高效、快速求解非均匀介质的声场值，因此本文采用此方法求解。弹性介质中二维声场特性的一阶速度-应力方程为[16]

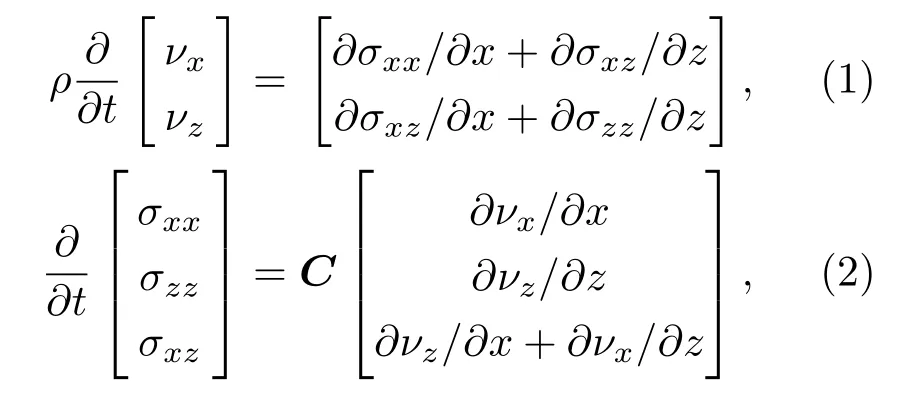
其中，σ表示质点应力；ν为质点的振动速度；ρ为介质密度；C表示介质弹性常数矩阵，

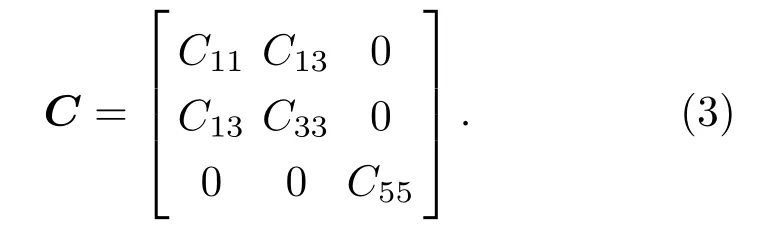
这里选取时间2 阶、空间4 阶差分精度，推导出一阶速度-应力交错网格声波方程格式为

式(4)中：变量下标表示空间位置，上标表示时刻；其中，

边界条件采用Clayton-Engguist-MaJda2 阶吸收边界条件[17]。

时域有限差分法利用近似的差分方程和上一时刻的波场值，计算出下一时刻的波场值，随着时间递推时，便能获得各质点处各时刻的波场值。

2 混凝土试件结构及测试装置布置

为了便于分析超声波在混凝土内部的传播特性，避免缺陷体之间的相互影响，本文以单缺陷体作为嵌入对象进行研究，如图1所示。混凝土尺寸为长40 mm，宽20 mm；混凝土为普通硅酸盐水泥加10%的混合材，砂石粒径不大于2 mm；缺陷体长度为10 mm，宽度分别设定为0.5 mm、1 mm、1.5 mm、2 mm、2.5 mm；混凝土密度为3000 kg/m3，缺陷体密度为1.24 kg/m3；超声波在密实混凝土中的纵波波速为6170.09 m/s，横波速度为3785.33 m/s，在缺陷体中的纵波速度为344.0 m/s，横波速度为0 m/s；超声波激励信号源采用应力加载的1 个周期的1 MHz 的正弦信号，信号源长度为1 mm 的线声源。

图1 混凝土结构模型Fig.1 Concrete structure model

为了保证超声信号能够更好的传播和接收，本文采用横向投射法，在混凝土模型一端垂直于端面设置超声波发射器，在另一端对应位置垂直于端面设置超声波接收器。

3 时域分析与讨论

超声波衰减公式为

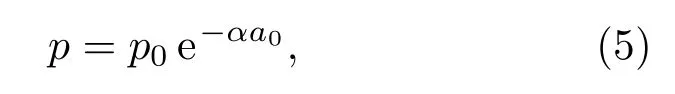
其中，p0为起始声压，p为距声源a0处声压，α为介质衰减系数，a0为超声发射器与接收器之间的尺寸，且a0为超声发射器与接收器之间密实体尺寸a密实体与缺陷体尺寸a缺陷体之和。

介质衰减系数α的尺度大小与材料性质、超声波频率有关。频率一定时，超声波在混凝土内部的密实体介质衰减系数α密实体与缺陷体介质衰减系数α缺陷体是确定值。当混凝土内部存在不密实缺陷体时，由于介质衰减系数α缺陷体的值远大于α混凝土，超声信号衰减主要受介质衰减系数较大的α缺陷体对应缺陷体尺寸a缺陷体的影响。

超声波信号在混凝土中传播时会发生衰减，混凝土的密实度会影响超声波信号的幅值大小，如图2所示。由于接收信号首波的第一个波谷和第一个波峰的幅值绝对值不相等，这里采用式(6)计算首波信号的平均幅值，

其中，amin为首波第一个波谷幅值，amax为首波第一个波峰幅值。

图2 混凝土有无缺陷体接收信号局部对比Fig.2 Local comparison of concrete receiving signals with or without defects

图3为无缺陷、0.5 mm 缺陷、1 mm 缺陷、1.5 mm 缺陷、2 mm 缺陷、2.5 mm 缺陷6 种情况下接收信号的首波波形，首波的平均幅值如表1所示。

从图4 可以看出，当混凝土内部存在开裂缺陷体时，接收信号时域幅值明显变小，信号衰减变大，接收信号幅值与缺陷尺寸大小呈指数衰减关系。

图3 不同缺陷体尺寸对应的超声接收信号Fig.3 Ultrasonic receiving signals corresponding to different defect width

表1 缺陷尺寸大小与平均幅值关系Table 1 Relation between defect size and average amplitude

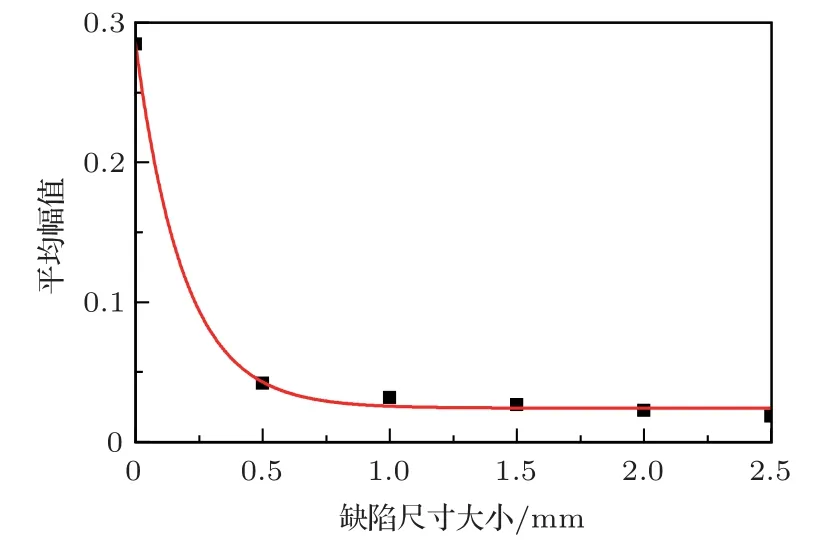
图4 平均幅值与缺陷尺寸大小的拟合曲线Fig.4 Fitting curve of average amplitude and defect width

另外，声波从声密介质到声疏介质、声疏介质到声密介质传播时会发生反射，特别是从声密介质到声疏介质传播时会发生较大的衰减，因此如图4所示，从无缺陷到有缺陷得到的接收信号幅值衰减比有缺陷之间的衰减要大很多。

从图5 可以看出，相对于无缺陷体混凝土试件，当试件存在开裂缺陷时，接收信号首波到达时间明显变长，接收信号传播时间与缺陷宽度呈线性关系。

图5 信号传播时间与缺陷宽度拟合曲线Fig.5 Fitting curve of signal propagation time and defect width

4 频域分析与讨论

为了进一步研究缺陷对频域的影响，需在频域提取出特征量。超声波在不同混凝土试块传播时，信号源采用同一频率的检测信号，该信号初始能量不变。由于初次到达端面的响应信号不受缺陷回波和端面回波的影响，因此，这里截取初次到达相对端面响应信号的时域信号。选取初次到达端面的响应信号的最大峰值对应的时间t峰为参考点，由于信号源周期T为1 μs，设定时窗为t峰-2T ～t峰+4T时，该时窗内频域能量占初次到达信号频域能量的绝大部分，因此选取这一时窗时可行的，如图6所示。对初次到达信号进行高频滤波和快速傅里叶变换，计算不同缺陷尺寸对应的频域能量。将接收信号频域能量进行归一化处理，将无缺陷混凝土试块接收信号频域能量设置为1，得到缺陷尺寸大小与归一化频域能量关系如表2所示。

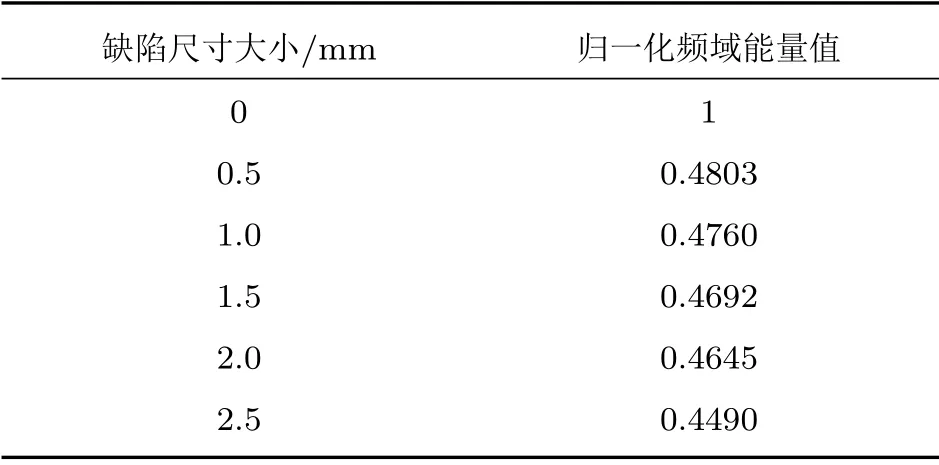
表2 缺陷尺寸大小与归一化频域能量关系Table 2 Relation between defect width and normalized frequency domain energy

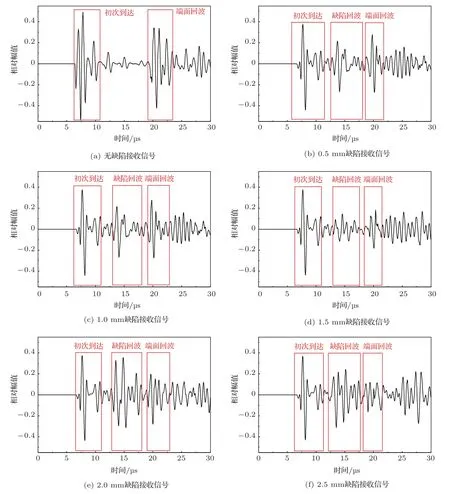
图6 混凝土有无缺陷体接收信号对比Fig.6 Contrast of received signals of defected concrete body with or without defects

图7 归一化频域能量与的缺陷尺寸大小拟合曲线Fig.7 Fitting curve of normalized frequency domain energy and defect width

从图7 可以看出，初次到达信号的频域能量与混凝土内部竖直开裂缺陷尺寸大小呈指数衰减。因此，利用初次到达信号的频域能量来进行混凝土内部裂纹尺寸大小预测是可行的。

5 结论

本文针对混凝土无损检测难以定量分析内部缺陷尺寸的问题，采用了时域有限差分数学模型，分别从时域和频域两个方面对混凝土超声波接收信号进行了研究，得出以下结论：

(1)当混凝土内部存在开裂缺陷时，接收信号时域幅值明显变小，信号衰减变大，接收信号幅值与缺陷尺寸大小呈指数衰减关系，且从无缺陷到有缺陷得到的接收信号幅值衰减比有缺陷之间的衰减要大很多；

(2)当混凝土试件内部存在开裂缺陷时，接收信号首波到达时间要比无缺陷时明显变长，有缺陷情况下信号传播时间与缺陷宽度呈线性关系；

(3)初次到达信号的频域能量与混凝土内部竖直开裂缺陷尺寸大小呈指数衰减，缺陷增大时，衰减变慢。