基于粒子群算法的稀疏阵列超声相控阵全聚焦成像

沈晓炜

(长沙理工大学汽车与机械工程学院 长沙 410114)

0 引言

随着制造业的进一步发展，工业产品零部件结构愈加复杂，复合材料[1]和新型制造技术[2]的使用比重不断上升，普通超声技术愈来愈难以胜任未来制造业的检测需求[3]。基于全聚焦的相控阵超声检测技术[3]自2005 年提出以来广泛应用于各个领域的无损检测与无损评价[4]，用于解决常规超声检测技术难以解决的问题[5]。随着工业领域对检测能力要求的不断提高，基于后处理的超声相控阵检测技术具有高灵敏度、高精度和高灵活性等特点[6]，在近十年来得到了长足的发展，其后处理成像算法越来越受到研究人员的重视，其中最具代表性的算法便是基于全矩阵数据的全聚焦成像算法(Total focusing method,TFM)。但是，基于全矩阵采集的全聚焦成像算法对数据量和计算时间的需求随着阵元数量的增加而呈指数增长，即便是16阵元的全矩阵采集数据量也超过了106个数，其巨大的计算量使得相控阵超声技术目前难以实现快速高精度的后处理成像。

面对日益增多的复杂结构件、复合材料构件以及3D 打印零件，单纯使用普通相控阵的线扫和扇扫已无法满足目前工业发展所需的检测要求。自全聚焦后处理算法出现以来，即便是满阵元的超声相控阵线性扫描或扇形扫描成像也达不到基于全矩阵全聚焦算法成像的效果[7-8]。与此同时，全聚焦算法已经成了检验其他后处理算法的黄金标准，而相控阵超声阵列如何有效进行稀疏优化和进行权值补偿达到全阵元全聚焦成像水准成了目前研究的难题。模拟退火算法[9]、遗传算法[10]、粒子群算法[11-12](Particle swarm optimization,PSO)在阵列优化相关领域中大放异彩，其中粒子群算法[13-14]具有极快的最优解逼近速度，其本质是利用当前位置、个体极值和全局极值参数指导下一步迭代位置，同时其算法简单，效率高，在传统天线优化领域应用极为广泛。但现有的研究集中于相控阵超声阵列普通波束的优化控制[15-16]，而稀疏阵列声场和后处理成像效果方面却鲜有提及[17-18]，如何快速高效地进行阵列稀疏优化和实现有效孔径补偿，是本文的研究目标。

本文提出了一种用于稀疏阵列全聚焦成像的阵列优化及阵元加权校正算法，并通过实际实验对该稀疏阵列的成像效果进行了验证。首先将稀疏阵列性能作为求解目标，在尝试已有文献提出的适应度函数上，利用主瓣宽度(Main-lobe wide,MLW)、旁瓣峰值(Peak side-lobe,PSL)以及主瓣峰值(Peak main-lobe,PML)作为约束条件构造适应度函数，计算得到最优化稀疏阵列分布和阵元权重系数，对实际缺陷试块进行稀疏阵列全聚焦优化成像，验证了算法的有效性，最后分析了目前所存在的不足之处并指出了下一步研究方向。

1 基于粒子群算法的稀疏阵列全聚焦成像算法

1.1 基于标准粒子群算法的线阵优化

对于数量为N的一维直线阵，阵列的远场方向图可表示为

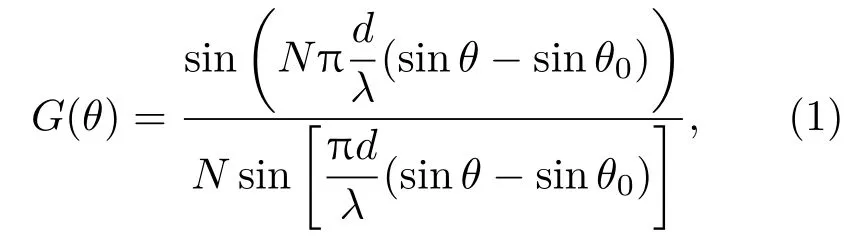
式(1)中：θ0为偏转角，θ为任意方向角，d为阵元间距，λ为波长。

利用标准粒子群算法将全阵元阵列稀疏所导致的栅瓣或高旁瓣权系数补偿问题转换为稀疏阵元权系数补偿优化问题，通过有限阵元的稀疏得到接近满阵元的指向性与全聚焦成像性能是PSO 算法的主要目标。通过将稀疏阵列的主瓣峰值、旁瓣峰值及主瓣宽度三个参数构造适应度函数，其中主瓣峰值和旁瓣峰值可以通过阵列方向图测出。基于粒子群算法对相控超声阵列的最优化过程表示为

(1)根据目标问题的转化，设置初始阵元数量为D(相控阵阵元数目)，阵列发射权重系数为xti(i=1,2,···,N)，阵列接收权重系数为xri(i=1,2,···,N)，学习因子c1=c2，惯性权重w，粒子个数N，最大迭代次数为Mk；

(2)构造适应度函数： fitness={0.8×(PML/PSL)2+0.2×(MLWSULA-MLW)2}作为阵列性能评价指标,式中MLWSULA为稀疏阵列均匀布置条件下的主瓣宽度。

(3)随机初始化粒子位置和速度，计算初始适应度；

(4)依粒子群迭代公式进行计算，不断更新个体最优值和全局最优值；

(5)计算完成后，输出最优化稀疏阵列放置位置及权重系数组合ωti(i=1,2,···,N)、ωri(i=1,2,···,N)，其中ωt为发射权重，ωr为接收权重。

在所述算法过程中，构造合适的适应度函数是保证PSO 算法收敛性和阵列优化效果的关键，在此验证了之前相关研究文章中所设计的适应度函数：

在计算过程中发现fitness1和fitness2所迭代出的稀疏阵列和算法收敛性效果欠佳，难以在迭代完成后得到理想的结果。

1.2 基于线阵权重补偿的全聚焦成像算法

考虑一维线性阵列探头放置于各向同性的均匀介质表面，模拟缺陷点散射体位于介质内部，建立基于全矩阵的全聚焦成像算法模型。基于全矩阵采集数据的全聚焦成像方法可有效实现全范围动态聚焦，具有极高的成像分辨率，然而全阵元收发数据量十分巨大，成像时间与数据量呈指数倍增长，全聚焦成像算法中点(x,z)的幅值可表示为

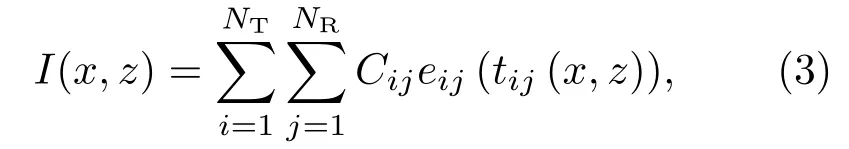
式(3)中，Cij为声波在楔块-试块传播时的总能量衰减校正系数，tij(x,z)为声波从第i个阵元传播至点(x,z)处并返回第j个阵元的时间，在各向同性介质中可表示为

根据文献[10,18]中所述研究结果，要使得稀疏阵列与全阵列性能一致，需要对收发阵元进行权重补偿，使得满足

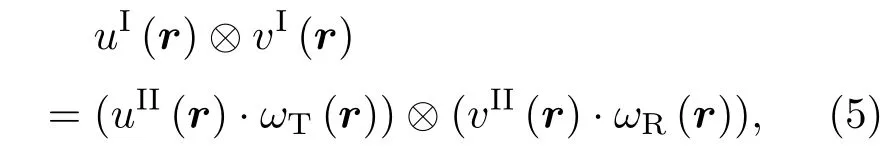
式(5)中，ωT、ωR为发射和接收阵元的权重函数，其中发射、接收阵元所对应的阵元的权重修正系数为ωi、ωj，将修正权值代入式(3)，得到修正后的全聚焦成像幅值：

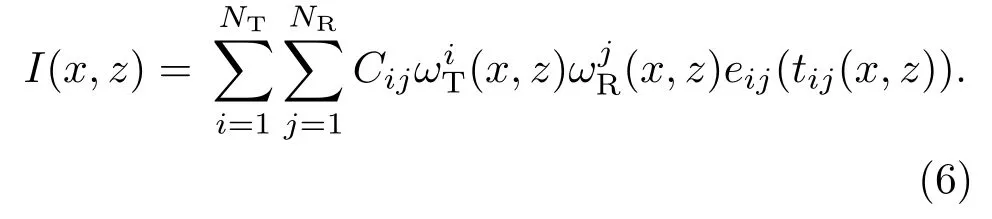
根据上述推导，提出基于稀疏阵列的全聚焦优化成像方法，如图1所示。

图1 稀疏阵列的全聚焦优化成像示意图Fig.1 Total focus imaging for sparse array with optimization

2 实验与全矩阵数据采集

以标准B 型相控阵试块上圆弧形分布且直径为2 mm的孔状缺陷为检测对象，检测区域如图2所示，缺陷大小及分布如图3所示。使用5L32-0.6×10型超声相控阵换能器，阵元数为32，阵元间距为0.6 mm，宽度0.5 mm，中心频率5 MHz，试块为钢材，声速为5900 m/s，通过全阵元逐次激励和接收进行全矩阵数据采集。

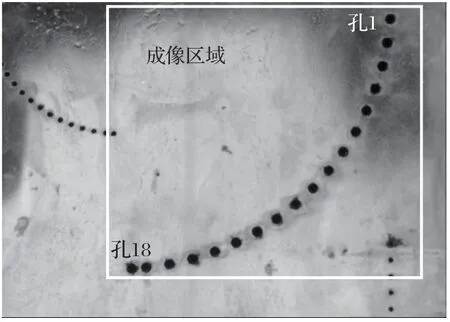
图2 检测缺陷区域示意图Fig.2 Schematic diagram of detection areas

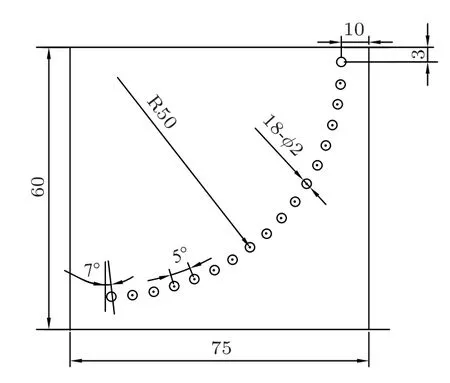
图3 试块缺陷尺寸图Fig.3 Defects size of specimen

3 结果与讨论

本文数据处理及成像计算设备为便携式计算机，单独使用CPU进行处理(GPU不参与运算)，型号为i7-8750h，6 核12 线程。首先针对试块缺陷，进行基于全矩阵采样数据的全聚焦成像，数据量为32×32×5120个，成像效果如图4所示。

通过对32 阵元线性阵列进行稀疏优化和权值修正，分别得到14 阵元和11 阵元的稀疏矩阵放置位置和权重修正系数，并对两个稀疏阵列分别进行稀疏全聚焦优化成像，如图5 和图6所示，成像数据量分别为14×32×5120个、11×32×5120个。如图中结果所示，优化后的稀疏阵列全聚焦成像在保证成像质量的同时，成像数据量分别减少了43.75%、65.62%。相控阵所在位置的近场伪影随着发射阵元数的降低而略微增加，这需要在之后的PSO 迭代函数优化、适应度函数优化、稀疏阵元有效孔径修正等方面进行深入研究。

为了进一步验证算法的有效性，分别使用14阵元、11阵元进行无权重补偿优化的稀疏阵列全聚焦成像(14 发射14接收，11发射11接收)，使用数据量分别为14×14×5120个、11×11×5120个，成像数据量相全阵元数据分别降低了80.86%、88.18%。成像结果如图7、图8所示，虽然主要缺陷仍然够进行识别，但是随着阵元的减少(数据量的降低)，在人工缺陷周围出现了明显的散射噪声和伪影，且近场区域噪声急剧增大，极大地降低了全聚焦算法的成像质量。考虑到阵元数量越少而成像质量越差的情况，选择11 阵元稀疏阵列进行阵元权值修正，优化后的全聚焦成像效果如如图9所示，人工缺陷附近的噪声和伪影得到了显著的抑制，成像质量基本达到了理想效果。但是，探头附近的伪影仅得到了部分消除，该问题难以通过阵元权值修正来解决。从数据压缩和传输角度分析，稀疏阵列全聚焦成像算法的成像数据量大幅降低虽然有利于未来检测数据的高度压缩和快速成像，但现有的成像算法在计算过程中仍然存在大量的冗余计算，使得成像效率偏低。因此，上述两个问题未来需要针对稀疏阵列的相控阵成像算法进行改进。

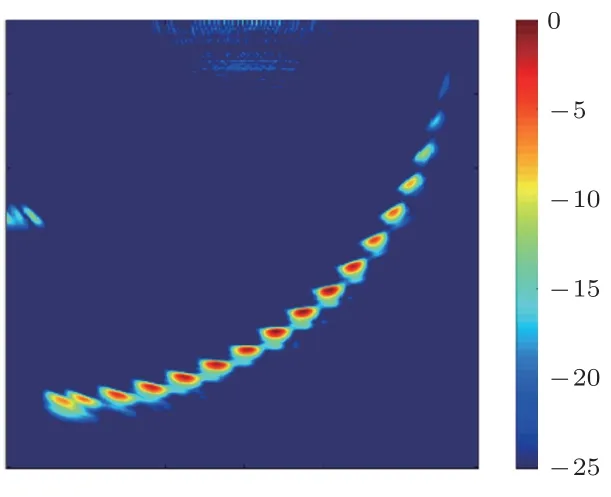
图4 全矩阵数据成像Fig.4 Full-element imaging

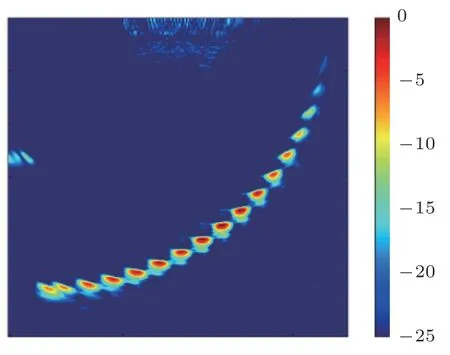
图5 PSO(14/32 阵元)稀疏阵元成像Fig.5 PSO(14/32 element)imaging

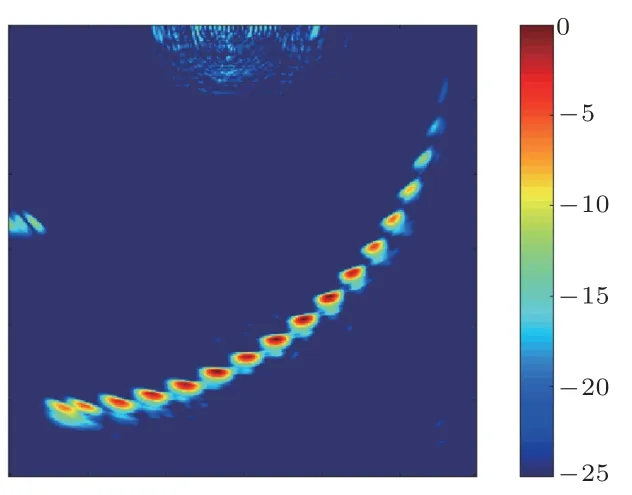
图6 PSO(11/32 阵元)稀疏阵元成像Fig.6 PSO(11/32 element)imaging

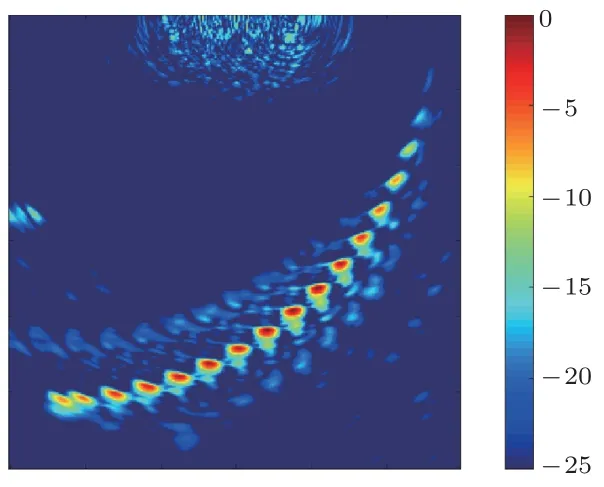
图7 PSO(14/14 阵元)稀疏阵元无优化成像Fig.7 PSO(14/14 element)imaging without optimization

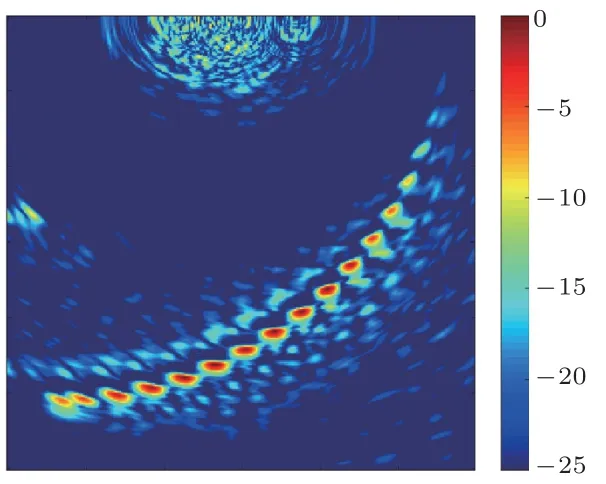
图8 PSO(11/11 阵元)稀疏阵元无优化成像Fig.8 PSO(11/11 element)imaging without optimization

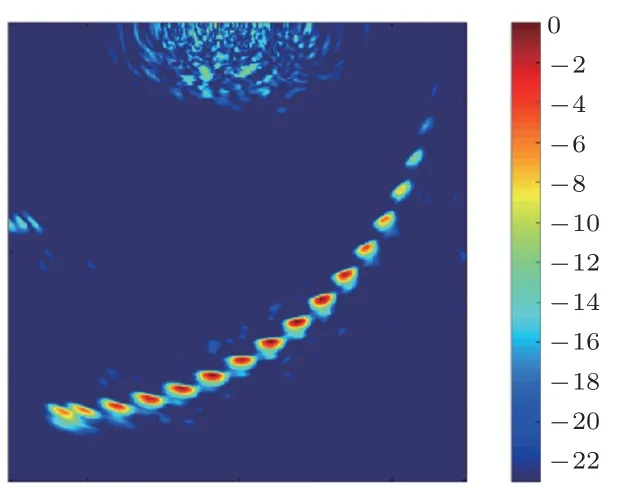
图9 PSO(11/11 阵元)稀疏阵元优化成像Fig.9 PSO(11/11 element)imaging with optimization

此外需要指出的是，当线阵进行稀疏处理后主瓣窄、旁瓣高，当稀疏阵列降低至14 个以及11 个阵元时，如图10、图11 及图12所示，稀疏阵列虽然在全聚焦成像上能够实现所需的检测及成像效果，但能否进行普通相控线扫和扇扫检测需要通过对不同类型缺陷试块进行验证。与此同时，随着移动处理器和5G 技术的高速发展，目前先进的相控阵超声检测产品已能实现实时的B 扫成像，因此普通扫查的速度优化已不是研究重点。因此，快速线扫、扇扫与高效率稀疏阵列相控阵全聚焦成像相结合的复合扫查将是未来的研究方向之一。

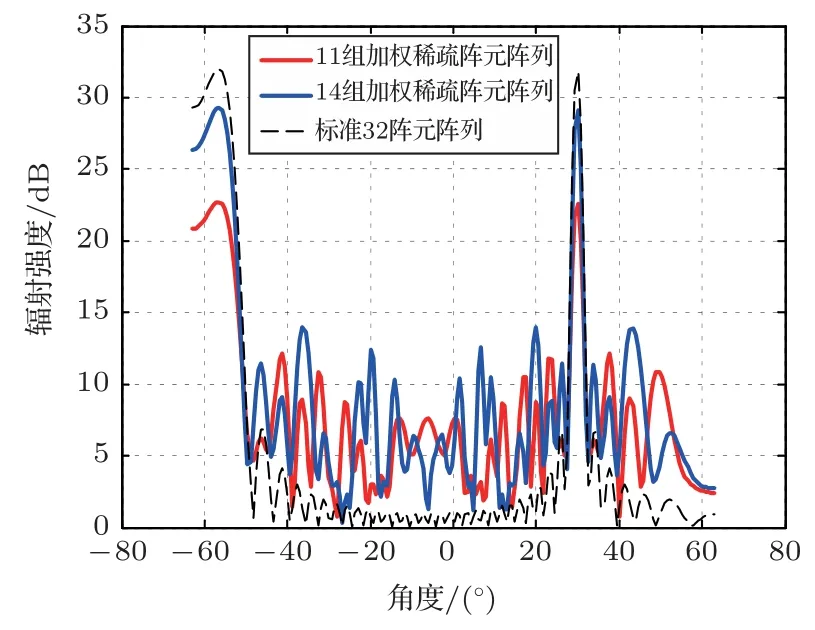
图10 稀疏阵列声束指向图Fig.10 Directivity diagram of sparse arrays

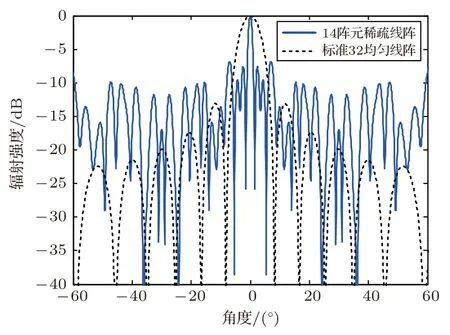
图11 14 元稀疏阵列的静态方向图Fig.11 Sparse array(14 element)static pattern

在阵列稀疏优化计算方面，利用利用PSO算法对阵列进行优化的时间最快仅为45 s(每50次迭代增加10 s)，而通过遗传算法进行计算达到了287 s，运算时间降低了84.86%。这是因为粒子群算法在计算问题上没有类似遗传算法的交叉和变异操作，大幅简化了迭代过程，在一般情况下效率远远超过遗传算法。PSO 算法虽然具有速度快、参数少、实现简单等特点，但是在收敛性方面还略有不足，在多约束条件下求解问题上容易出现局部最优解的问题，可能在最终迭代结束后得不到最优解，这可以通过算法的进一步优化或使用混合优化算法(如粒子群-遗传)来解决。另一方面，虽然目前粒子群算法、模拟退火算法、差分进化算法等优化算法在阵列稀疏和阵元布置方面存在较多的理论成果，但在超声检测领域，特别是在超声相控阵的快速成像、相控阵稀疏阵列的适应度函数设计、非均匀阵列孔径补偿等方面的研究和应用仍然较为薄弱。

此外，在实际应用中，还需要考虑各向异性材料、试块表面质量、近场缺陷和不同种类缺陷识别的问题，这也是稀疏相控阵进行实际检测和后处理成像时需要考虑的因素。

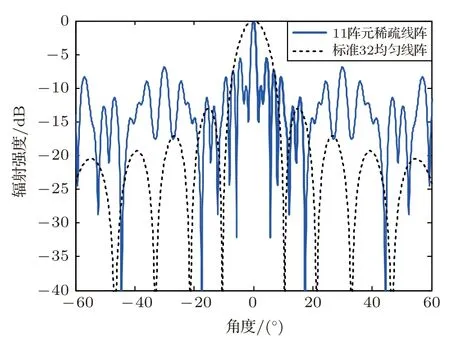
图12 11 元稀疏阵列的静态方向图Fig.12 Sparse array(11 element)static pattern

4 结论

本文使用粒子群算法，将最小化主瓣宽度、旁瓣峰值以及主瓣峰值作为约束条件构造适应度函数，求解得到最佳稀疏阵列和阵元权重修正，并验证了所求阵列在后处理全聚焦算法成像中的成像效果。相比于满阵元全聚焦成像算法，稀疏发射-全阵元接收的阵列组合在保证人工缺陷检测成像效果的同时，降低了阵元使用数量和数据量，而全稀疏阵列(稀疏发射-稀疏接收)阵列组合进一步降低了成像所需的数据量。相比于现有的稀疏阵列优化算法，计算速度得到了极大的提高，且经过算法优化后的全矩阵数据稀疏度可达到85%以上，有利于之后利用压缩传感进一步提高数据传输效率和成像效率。但标准粒子群算法的迭代函数、适应度函数、和稀疏阵元权重修正系数还需要进一步的设计与优化，以确保其具有可靠的收敛性能和更好的成像性能。使用稀疏阵列进行后处理成像时，未参与计算的回波数据被直接忽略而未得到有效利用，可能会影响细小缺陷和闭合裂纹的检测效果。此外本文所述方法有效降低了成像数据的使用量，从理论上提高了数据传输性能和成像效率，但现有的成像算法无法解决稀疏阵列成像的近场成像伪影问题，且在成像过程中存在大量的冗余计算，这需要针对稀疏成像算法进行改进以提高成像效率。