基于近场辐射声压信号的索力识别方法*

余忠儒 邵 帅 周志祥 邓国军 王邵锐 简传熠

(1 重庆交通大学土木工程学院 重庆 400074)

(2 深圳大学土木交通工程学院 深圳 518061)

0 引言

拉索常用于斜拉桥、悬索桥及拱桥等大跨径桥梁工程体系中，随着建筑结构规模的不断扩大，拉索结构也越来越广泛地运用于大跨度空间建筑工程中[1]。拉索作为桥梁结构中关键的受力构件，索力的分布与改变会对桥梁的内力分布以及桥面线形产生较大影响。索力的准确、方便、快速测量成为评价桥梁结构施工质量与运营期间桥梁结构健康状况的关键指标。如何对索力进行快速精准的测量成为一个关键问题[2]。

目前，针对索力的测量已有多种方法，主要包括压力传感器法、压力表法、频率法、磁通量法以及以三点弯矩法为代表的静力测试方法等。传统测试方法或多或少存在些许不足。压力传感器法和压力表法虽然能较为准确地测量出拉索索力，但是其传感器昂贵，仪器笨重且只适用于施工阶段索力的测试；磁通量法性能稳定、精度高，但其标定复杂，且对在役结构需现场绕制传感器，成本较高；静力测试方法简单易用，相关学者也对其进行了深入研究与仪器开发，但静力测试方法只适用于小直径钢索，测试误差随钢索直径增大而增大。频率法因其操作简单、经济实用而广泛运用于工程实际中[3]。传统频率法基于精密拾振器，通过与被测物接触，拾取拉索在环境或者人工激励下的振动信号经由频谱分析得出拉索固有频率以确定拉索索力。由于拾振器粘附在结构物上，其自身重力将会导致结构产生附加质量，从而显著影响结构模态参数识别；此外，在某些特殊位置及环境下，传感器布置困难，通过传感器难以获取结构响应[4]。基于激光拾振仪、微波雷达、高速摄影机和近场声压的非接触测量技术由于其非接触、仪器布置方便以及响应速度快等优点而越来越受到重视。相关学者针对声压测量获取结构振动响应也做了大量研究，Prezelj等[5-6]利用置于振动结构的非常近的场中的单麦克风，对结构近场声压进行测量，并采用离散Rayleigh 积分方法反演实现了对结构表面振动模态的重构。Zhu等[7]通过有限元方法建立声固耦合的动力学方程，成功识别结构模态参数，现有方法测得的固有频率与有限元测得的固有频率之差均小于3%，相关振型的模态保证判据值均大于90%。夏茂龙等[8]利用结构振动近场辐射声压信号，成功对一平面钢板的固有频率和模态阻尼比进行了识别，为工程结构的模态参数识别提供了新的方法。

本文提出利用结构近场固定位置声压信号对拉索进行快速、准确索力测试的方法。根据振声互易定理，结构振动近场声压响应等价于利用传感器获取的结构振动加速度响应，避免了加速度传感器自身重力对结构固有频率测试的影响。以单根拉索为例，通过对结构中心表面处施加一瞬时脉冲力，使拉索受迫振动发声，并对结构近场范围内拉索振动辐射声压进行测量，以获取不同工况下不同位置结构近场声压信号。对原始声压信号添加高斯白噪声，利用希尔伯特-黄变换(Hilbert-Huang transform,HHT)方法分析并结合索力计算实用公式准确识别出结构固有频率和计算出拉索索力值，并探讨了索力识别结果随测试距离变化和测试位置改变的影响。

1 基本原理

1.1 脉冲激励下拉索结构动力响应

对于一个多自由度体系其结构动力学方程可表示为

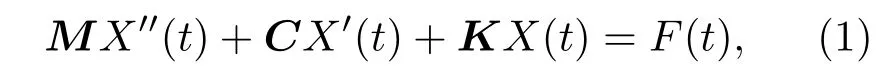
其中：M表示结构质量，C为阻尼，K表示刚度矩阵，X(t)表示结构位移响应，F(t)为脉冲力。假设结构存在正态振型，则结构的位移和加速度响应可表示成各阶模态响应的线性叠加：

其中：Φj表示结构的第j阶模态振型，为正交矩阵，qj(t)表示结构的第j阶模态坐标。假设结构为比例阻尼，将式(2)带入式(1)利用模态坐标表示存在解耦的结构运动方程为

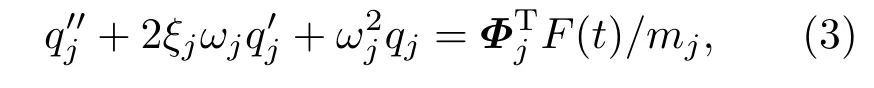
其中：ωj表示结构的第j阶模态频率；ξj表示结构的第j阶模态阻尼比；mj表示结构的第j阶模态质量。作用在结构上某点h的脉冲激励fk(t)=F0δ(t)，其中fj(t)表示F(t)矩阵的第j个元素，则利用模态坐标表示结构响应的第j阶加速度为[9]

其中，

式(6)中，φpj,k表示结构在第j阶模态振型中点p与点h的相位差。

1.2 结构振动近场辐射声压

结构在瞬时力F作用下受迫振动，之后以某一频率ω自由振动，产生的振动波在空气中传播引起空气流体介质中某点压强pd的变化，该过程可以看作结构对空气流体的单向耦合作用。本文针对拉索结构，将拉索沿长度方向划分成有限多个单元，拉索在脉冲力作用下将会发生受迫振动，类似于吉他拨弦振动发声，此时每一个单元可以看作一个点声源。声场中靠近结构某点的声压变化可看作只由该点振动产生的声辐射引起[10]，如图1所示。

由结构某点振动作为声源，结构近场声压变化表示为p(d,t)，对于拉索结构振动的法向速度与法向加速度表示为[5]

其中，ρ0表示空气密度，表示结构振动体积速度振幅，w表示波数。假设结构振动声源的表面积大小为S，表示为

将式(11)带入式(10)，并结合式(8)、式(9)之间的关系，令，则结构近场声压变化表示为

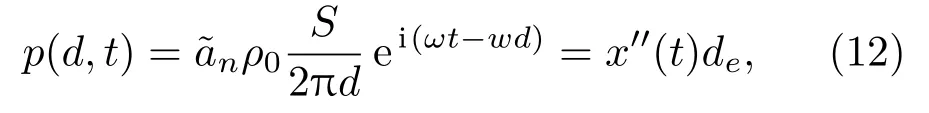
其中，de为常数项，结构近场声压与声源振动的加速度存在线性比例关系，即可以说明利用结构近场声压变化可以反映结构振动响应。

图1 结构原理示意图Fig.1 Schematic diagram of structure principle

2 基于HHT的近场声压信号频域分析

为确定结构固有频率，需对结构振动响应时域信号进行频谱分析。由于结构振动所产生的声压信号在实际测量中具有非线性、非平稳的特点，而传统谱分析方法要求系统具有线性或者数据具有周期、平稳的特点，否则分析结果往往不具有任何物理意义。

Huang 等[11]通过对大量数据进行分析提出基于经验模态分解(Empirical mode decomposition,EMD)的Hilbert 变换方法，用以分析非线性、非平稳数据，并得到原始信号相关振幅、瞬时频率和相位。该方法关键部分在于EMD，即任何复杂数据集都可以分解成有限个且数量很少的固有模态函数(Intrinsic mode functions,IMF)，该分解方法是基于数据在时间尺度上的局部特征，并且是自适应的。这些有限数量的IMF具有良好的Hilbert变换特性，并满足以下两个条件：(1)在整个数据集中，极值点数目和过零点数目相等或最多相差1；(2)由局部极大值确定的包络线和局部极小值确定的包络线的均值均为0。

由上述知结构近场某点测量声压为pd(t)，基于EMD将原始声压信号分解为有限个固有模态函数:

将原始声压信号分解并表示为n个固有模态函数xi(t)求和的形式；rn为残差，表示一个常数或平均趋势。Hilbert变换后的IMF表示如下：

其中，P表示柯西主值，x(t)与y(t)形成复共轭对，其解析信号可表示为

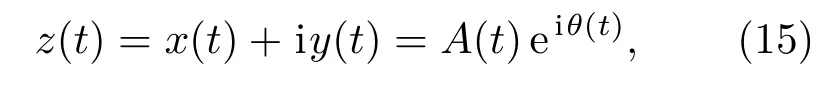
由式(16)可知，瞬态频率表示为瞬态相位角θ(t)随时间变化的斜率。结构近场一点的声压响应pd(t)经过EMD 分解以及Hilbert 变换可以得到其相应的解析信号，且由式(12)可知，结构近场某点声压频率和结构振动频率吻合，以此通过对结构振动近场声压的测量得到结构振动频率是可行的。

此外，当被分解信号中混有异常信号时，尤其是强噪声干扰信号和高频噪声信号，经过EMD 分解后会产生模态混淆，即在某一个IMF 分量中包含不同的特征时间尺度成分。为此，Yang 等[12]提出在进行经验模态分解前，首先对数据进行滤波处理。本文采用切比雪夫I 类带通滤波器对原始声压信号进行滤波处理，通过对原始声压信号进行快速傅里叶变换(Fast Fourier transform,FFT)，大致确定各阶频率带通范围，然后再以滤波后的信号作为EMD信号输入进行后续处理。

3 索力计算

通过对结构近场某点声压进行测量，得到声压变化时程曲线，采用HHT 方法对测量声压信号进行频谱分析，以获取结构振动频率。索力测试依赖于弦振动和梁振动理论，通过建立拉索结构振动频率和两端张力之间关系，从而可以用结构振动频率推算出索力大小。根据《公路桥梁荷载试验规程》[13]，利用频率法对拉索进行索力测试，拉索索力计算实用公式由式(17)给出，该公式不仅适用于长细比较大的情况，在长细比L/D＜70 的情况下依旧能得到较好的测试结果，结果平均误差小于2%。

其中：fn表示拉索的第n阶固有频率，EI 表示抗弯刚度。若不考虑拉索抗弯刚度，式(17)可写成

对于给定拉索结构，其单位长度质量m、索长L以及抗弯刚度EI已知，通过对结构振动信号分析获取索振动频率并结合式(17)即可推算出索力大小。具体流程图如图2所示。

图2 索力识别流程图Fig.2 Cable force identification flow chart

4 数值模拟及分析

4.1 计算模型

本文通过对空气声压场中一根拉索进行有限元模拟，考虑结构对空气的单向耦合作用，有限元相关参数如下：索长L=5.0 m，拉索截面为圆截面，直径d=0.02 m，线密度ρl=2.466 kg/m，杨氏模量E=2.1×1011Pa，泊松比ν=0.3，结构周围空气场直径D=10 m，完美匹配层(Perfectly matched layer,PML)厚度Dp=1.0 m，空气密度为ρa=1.293 kg/m3，空气场温度为15°C，气压为一个标准大气压，相应声速为343 m/s。对拉索两端分别施加20 kN(I)、30 kN(II)和40 kN(III)三种不同工况的拉力，并考虑拉索结构两端支撑形式为固定约束。为方便有限元建模，结构阻尼假设为比例阻尼，阻尼比为0.01，建模相关参数如表1所示。结构有限元模型如图3所示。

表1 有限元模型参数Table 1 Finite element model parameters

图3 有限元模型示意图Fig.3 Schematic diagram of finite element model

4.2 仿真结果与分析

拉索结构在0 时刻无初始加速度，现对拉索结构中心位置表面O(x=2.5 m,y=0 m)处施加一瞬时斜坡荷载，峰值力F=100 N，为得到结构振动响应瞬时信号，对结构近场声压变化进行采集，采样频率为1000 Hz，持续时间为4 s。以拉索承受20 kN拉力为例，选取垂直于点O(x=2.5 m,y=0 m)近场位置中0.1 m、0.2 m、0.3 m处的3点，得到结构点O加速度时程响应以及近场中声压变化瞬时响应信号如图4所示。

图4 加速度及不同位置声压变化时程曲线Fig.4 Time history curve of acceleration and sound pressure change at different positions

由图4 可知在无噪声情况下，结构振动加速度响应与近场辐射声压响应具有相同的趋势，与理论推导相一致。在实际测试过程中，结构振动辐射声压信号往往会受到环境噪声干扰，为模拟信号受到噪声干扰的情况，现在对结构辐射声压信号添加高斯白噪声，并基于FFT 大致确定频率响应范围。对上述0.1 m 处近场处辐射声压信号添加信噪比为0.5 的高斯白噪声，并由FFT 分析得到一阶频率响应范围5 Hz ≤f≤15 Hz，噪声信号及添加噪声后的声压信号如图5、图6所示。采用切比雪夫I 类带通滤波器对声压响应信号滤波处理并进行EMD分解，选取第一阶IMF 分量进行Hilbert 变换，计算得到瞬时相位，以及对应Hilbert 边际谱如图7～10所示。

图5 高斯噪声信号Fig.5 Gaussian noise signal

图6 有噪声干扰声压信号Fig.6 Noise interference sound pressure signal

图7 傅里叶频域谱Fig.7 Fourier frequency spectrum

图8 第一阶IMF 分量Fig.8 First order IMF component

图9 瞬时相位Fig.9 Instantaneous phase

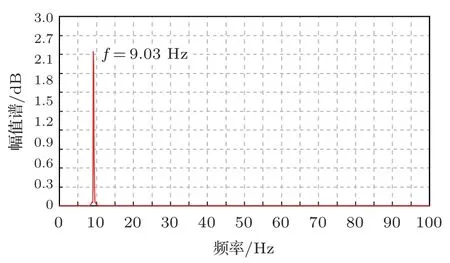
图10 Hilbert 边际谱Fig.10 Hilbert marginal spectrum

根据图9 瞬时相位角并利用式(16)以及Hilbert边际谱可得到结构固有频率为f=9.03 Hz。采用相同方法分别对不同工况下结构近场0.1 m 位置处声压信号进行处理并与有限元法特征频率分析得到的结构固有频率进行对比，结果如表2所示。

表2 不同工况下结构固有频率Table 2 Natural frequency of structure under different working conditions

由表2 知，本文利用HHT方法计算得结构固有频率与理论值接近。按照相同步骤处理距离结构表面0.2 m、0.3 m 距离处声压信号，并利用公式(18)计算出索力值，结果对比如表3所示。

表3 不同位置声压信号所得频率与计算索力Table 3 Frequency and cable force of different position sound pressure signal

对比分析表3，结果表明，利用结构近场辐射声压信号通过HHT 方法能较为准确地识别出结构固有频率，并且在0.3 m距离范围内保持较高精度。利用结构固有频率并结合公式(18)推算出拉索索力值也能达到较高精度，平均误差在1%以内。为验证本文方法的适用性，另外任取两点A(x=2.8 m,y=0 m)和B(x=3.0 m,y=0 m)垂直距离上0.1 m、0.2 m、0.3 m处的结构辐射声压响应，并利用本文所述方法分析得到相应频率值和拉索索力，结果如表4所示。

表4 A、B 点不同位置声压信号所得频率与计算索力Table 4 Frequency and cable force of sound pressure signal at different positions of points A and B

由表4 计算结果可知，利用结构近场辐射声压信号通过HHT 方法在0.3 m 范围能较为准确地识别出结构固有频率，并结合索力计算实用公式能较为准确地计算出拉索索力值。

上述方法通过数值分析证明了其可行性和有效性，并在有高斯白噪声干扰情况下也能得到较好的测试效果。但在实际试验中，噪声信号往往复杂多变，环境中的高频噪声以及高能噪声会对测试结果造成很大的影响，使得声音信号产生混淆，导致对声音信号分析处理后较难得到准确的频率值，进而影响索力测试结果；另一方面，从测试结果可以看出，声压信号能量较低，在实际试验过程中容易被其他噪声信号覆盖淹没。针对以上测试过程可能遇到的问题，课题组开展相关研究，考虑如何对复杂环境噪声剔除、数据与信号深度挖掘以增强有用信号，改进及优化该方法的抗噪性和抗干扰性能，提高测试信号信噪比及稳定性。

5 结论

本文提出利用结构近场固定位置声压信号并结合Hilbert-Huang 变换对拉索进行索力测试的方法。通过理论推导了结构加速度响应与结构近场辐射声压响应的线性关系，结合HHT 推导出声压响应信号与结构频率关系，并利用索力计算实用公式计算出拉索索力。对一根5 m 长拉索进行有限元数值模拟，分别测试了在不同工况和不同测量位置下该方法的有效性，结论如下：

(1)本文利用结构近场辐射声压信号作为分析信号，具有非接触的特点，避免了因加速度传感器自身重力对结构固有频率测试的影响，并在测试过程中能准确、快速、方便地获取拉索振动固有频率和索力值。

(2)结构振动所产生的声压信号在实际测量中具有非线性、非平稳的特点，结合HHT 能有效处理结构辐射声压信号，并准确获取结构固有频率，结合拉索索力计算实用公式能准确计算索力值。在结构近场0.3 m范围内，不同工况、不同位置声压测量信号处理得到的结果都具有较高的准确性。

(3)本文仅通过数值模拟分析并验证了该方法在拉索索力识别的可行性与有效性。在后续试验及实际应用过程中如何提高算法的抗噪性能，有效剔除干扰信号及其适用性尚待进一步研究。