求解非线性分数阶偏微分方程精确解的几种方法

张 慧

(西南科技大学城市学院 通识教育学院，四川 绵阳 621000)

生活中许多问题的数学模型最终都可以归结为整数阶微分方程的定解问题，整数阶微积分无论在理论分析还是数值求解方面的发展都相对比较完善.如：刘倩等[1]研究了一类非线性电路方程的行波解,房春梅[2-3]研究了Backlund变换问题，敖特根[4]构造了非线性发展方程的一种新形式解.然而，整数阶微分方程求解领域的现有方法，无法直接应用到分数阶微分方程求解领域中去，所以目前求解分数阶微分方程的方法相对较少.

随着分数阶微积分理论的发展，力学、工程技术学、物理学、生命科学和应用数学等领域的工作者越来越关注分数阶偏微分方程的解法的研究.近几十年来，陆陆续续提出了许多有效的求解方法，包括格林函数法[5]、Adomian分解法[6]、首次积分法[7]、同伦函数法[8]、李群理论方法[9]、不变子空间方法[10]、分式变分迭代法[11]、分数复变换法[12]、分离变量法[13]、Laplace变换法[14]以及分离变量法与齐次平衡原理相结合的方法[15]等等.

然而，上述方法各自既有优点，又有局限.对于更加复杂的分数阶微分模型，并不存在哪一种方法具有普遍的适用性.本文将采用3种不同的方法分别求解时间分数阶扩散-对流微分方程，通过分析得到的各类精确解的动力学性质，比较3种方法的利弊.

1 分数阶扩散-对流方程的精确解

分别使用不变子空间法、变量分离与齐次平衡相结合的方法以及齐次平衡与积分分支相结合的方法来研究时间分数阶扩散-对流方程[16]的精确解：

(1)

其中f(u)和g(u)分别是扩散和对流项，为了说明方便，将考虑具体形式进行讨论.令f(u)=u,g(u)=k1为常数，可以得到以下时间分数阶偏微分方程：

(2)

1.1 不变子空间法

考虑子空间W3=L{1,x,x2}，于是可得如下形式的精确解：

u(x,t)=C1(t)+C2(t)x+C3(t)x2，

(3)

其中C1(t)、C2(t)、C3(t)为待定函数.将式(3)代入式(2)，让x的同次幂的所有系数都等于零得：

(4)

求解方程组(4)可得：

(5)

于是可得方程(2)的一个精确解为：

(6)

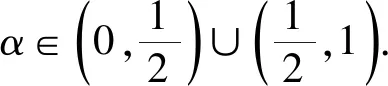
1.2 变量分离与齐次平衡相结合的方法

假设方程(2)有如下形式的解[17]：

(7)

u(x,t)=a0tγ0+a1tγ1x+a2tγ2x2.

(8)

其中γ0、γ1、γ2、a0、a1,a2为待定常数.将式(8)代入方程(2)中得:

(9)

在式(9)中让t的所有幂指数相等，可得:

γ0-α=γ1-α=γ2-α=2γ1=γ0+γ2=γ1+γ2=2γ2.

(10)

求解式(10)可得:

γ0=γ1=γ2=-α.

(11)

在式(9)中，利用齐次平衡原理，让:

(12)

求解式(12)得:

(13)

将式(11)和式(13)代入式(8)，可得方程(2)的一个精确解为:

(14)

其中a1为任意常数.

1.3 齐次平衡与积分分支法相结合的方法

假设方程(2)具有下列分离变量类型的精确解[18]:

u(x,t)=[a0+a1v(x)]tγ.

(15)

将式(15)代入式(2)得:

(16)

根据齐次平衡原理，让式(16)中所有t的幂指数相等可得：

γ-α=2γ.

(17)

解得γ=-α，再将其代入式(16)并消去t-2α可得:

(18)

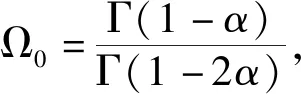
(19)

dx=(a0+a1v)dτ,

(20)

其中τ是一个参数，因此，系统(19)可以简化为一个规则的平面系统:

(21)

显然，系统(21)和(19)有相同的首次积分:

(22)

其中h是一个积分常数.方程(22)可以改写为:

(23)

接下来，利用积分分岔法，将分情况讨论(2)的精确解.

情形1a0≠0,h=0，方程(22)可化简为:

(24)

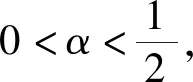
(25)

(26)

其中c1为任意常数，且常数a1≠0.将式(26)与γ=-α代入式(15)可得方程(2)的一个精确解:

(27)

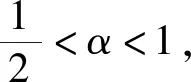
(28)

(29)

其中c2为任意常数，且常数a1≠0.将式(29)与γ=-α代入式(15)可得方程(2)的另一个精确解：

(30)

(31)

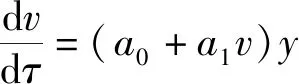
(32)

对式(32)积分并且令积分常数为零可得:

(33)

(34)

其中E(ω1τ,k1)是第二类椭圆积分函数，将式(33)和a0=0代入式(15)，再联立式(34)式可得方程(2)的一个精确解:

(35)

其余情况也类似处理，本文不作讨论.

2 结语

本文利用不变子空间法、变量分离与齐次平衡原理相结合的方法、齐次平衡与积分分支相结合的方法分别求解时间分数阶扩散-对流微分方程的精确解.通过对这些精确解的动力学性质和动力学行为详细分析后发现，当时间t趋于正无穷时，t-α趋近于0，故解u具有随时间t的增加而衰减的特性；从精确解的类型来看，不变子空间法与变量分离与齐次平衡原理相结合的方法所得的精确解类型比较少，计算过程相对比较简便；而齐次平衡与积分分支相结合的方法所得精确解的类型比较丰富，包括参数形式的解、周期形式的解和幂函数形式的解、椭圆积分函数形式的解，更容易分析方程的物理意义，但是其计算相对比较复杂.因此这些方法虽然都能够求解分数阶微分方程的精确解，但是各有利弊，可以根据需求选取相应的求解方法.