基于CEA+Boruta模式的特征选择算法
朱颢东,常志芳
(郑州轻工业大学 计算机与通信工程学院,郑州 450000)
随着大数据时代的到来和存储技术的快速发展,使得各个领域产生和收集数据变得越来越容易,但所获数据中充斥的噪声和冗余也日益增加[1].特征选择也称属性选择,即从原始特征中选择出最有效特征来降低数据集的维度的过程[2].由于特征选择具有良好的去除噪声和冗余能力,是数据预处理的关键步骤,所以成为机器学习与数据挖掘领域中研究的热点问题[3].一个好的特征选择算法不仅能显著降低特征维数,而且能提高计算效率和预测性能[4].李杨等[5]曾提出一种基于改进mRMR和支持向量机的特征选择方法,他通过引入特征相关冗余权重因子改进mRMR能有效细化对特征相关性和冗余性的平衡和度量,大幅度降低原始样本集的维数.王波等[6]针对小样本数据特征选择问题提出了一种MIFS-Boruta算法.李占山等[7]借鉴极端提升算法,通过改进的序列浮动前向搜索策略搜索特征子集,以此获得最优特征集.陈磊等[8]结合二分法与BP神经网络对牛乳体细胞进行识别提高了计数识别率.孙桂煌[9]在机器学习算法下结合模糊度特征提取和三维空间重组方法对细节特征进行识别,改善了人体动作信息检测和辨别能力.还有许多学者在特征选择方向上研究出适用不同情境下的特征选择算法.
特征选择算法通常分为过滤式(filter)、封装式(wrapper)、嵌入式(embedded)三大类[10].过滤式是通过评价每个特征与文本的相关性和发散性程度,设定合适的阈值筛选出最相关的特征集.它不需要借助机器学习算法即可快速排除一部分非重要噪声特征,缩小优化了特征子集搜索范围,但难以发现特征间潜在相关性,不能选择出一个较优且规模较小的特征子集[11].典型的过滤式有方差选择法、相关系数法、卡方检验、信息增益和互信息法.封装式是利用特定模型的学习结果作为衡量特征间重要程度的标准,如遗传算法,递归特征消除法(recursive feature elimination,RFE)、Boruta法.该类方法考虑到了特征间的相互作用,所选的优化特征子集规模相对较小,但计算效率远远不如过滤式方法.由于封装式特征选择方法搜索空间大,通常需要学习算法的介入,时间复杂度较高导致计算量太大[12],泛化能力也比较差.嵌入式是用机器学习中模型适应和训练特征全集,以最优的目标函数判断特征的去留.在sklearn中,使用Select From Model函数将各个特征的权值系数计算出来,根据系数从大到小选择特征.最常用的是使用GBDT、L1正则化和L2正则化来选择特征.不少学者基于这三类方式在不同领域中加以融合和改进,并通过机器学习算法验证数据集的分类准确率[13].陶勇森[14]融合信息增益与和声搜索算法对语音数据集进行特征选择提高了语音情感分类效率.许行等[15]在过滤阶段定义了基于互信息的特征分组标准有效去除不相关和冗余特征,结合Boruta算法为解决小样本问题提供了一种有效的方法,但是该算法不能自动确定合理的候选特征子集.周传华等[16]基于filter和wrapper模式提出了FSIGR算法,为数据降维问题奠定了理论基础,但是较少的考虑特征之间的相关性.
本文将基于封装式的Boruta算法,提出一种新的两阶段特征选择算法.在第一阶段,使用CEA过滤选择方法找到候选特征集;在第二阶段采用改进的Boruta算法从候选特征集中筛选出最优特征集合,解决传统算法时间复杂度较高,较少考虑特征之间相关性等问题,该算法在python中有相应的模块用于特征显著性的挑选,可以在代码中直接调用,十分方便.
1 预备知识
1.1 Boruta特征选择算法
Boruta算法是特征选择方法中一种利用随机森林作为分类器的封装式算法,主要通过平均减少精度值来筛选出与因变量具有相关性的特征集合,boruta_py是sklearn中的扩展包,在python中易于实现.对于特征变量较多甚至超过样本数目的数据集,使用传统回归等方式会导致过拟合问题,因此,本文借鉴Boruta算法思想提出一种新的特征选择方法.传统的Boruta算法思想如下[17].
第1步:创建阴影特征,对每个真实变量R,随机打乱后排列,将所有变量的副本构建成随机组合的阴影特征矩阵S,拼接到真实特征后面,构成新的特征矩阵N=[R,S].
第2步:用新的特征矩阵N作为输入,在监督模式下,随机森林作为分类器训练一个扩展数据集,取阴影特征重要性的最大值smax,真实特征中重要性大于smax的,记录一次命中,并采用平均减少精度以评估的每个特征的重要性,越高则意味着对预测结果的贡献越大[18].
第3步:在每次迭代中,它检查一个真实特征是否比最好的阴影特征具有更高的重要性(即该特征是否比最大的阴影特征得分更高)并且不断删除它视为非常不重要的特征,重复该过程[19].
第4步:直到遍历过的所有特征得到“拒绝”或者“接受”的分配结果,或者达到先前设置的随机森林运行的迭代次数时,算法停止.
1.2 综合评估算法(comprehensive evaluation algorithm,CEA)
第1步:计算数据集中每个特征的信息增益比值GR,当GR等于0,认为该特征与类别不相关,并从数据集中剔除.
第2步:从分类能力和信息相关性两方面通过计算数据集中每个特征的平均准确率降低值(MDA)和信息增益比值(GR),来对每个特征进行重要性度量.
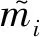

2 CEA+Boruta算法
2.1 CEA+Boruta算法思想及设计
CEA+Boruta特征选择主要分为两个阶段:过滤阶段和封装阶段.在过滤阶段使用综合评估CEA算法,在封装阶段使用Boruta算法.
首先采用CEA算法计算出相应的平均准确率降低值和信息增益率值,通过标准化处理得到每个特征的综合评估值,以此对原始特征进行过滤和综合性评估,从不同的维度增强对特征的度量,删除无关特征,降低特征空间维度,提高了算法的运行效率,选出了最优的候选特征集.其次,采用改进的Boruta算法,根据先前设定好的迭代次数,通过控制阴影特征样本的比例并只对部分样本打乱后随机排列,以此来降低样本的复杂度,进而利用训练的随机森林分类器对每个特征的重要性(置换单个变量,认为导致随机森林的准确性下降幅度较大的变量对于数据分类更为重要)进行打分,计算出候选特征子集中每个特征的重要性从而去除不重要的特征,筛选出所有与因变量具有相关性的最优特征集合,解决了只用传统Boruta算法计算时间长,复杂度较高的问题.
2.2 CEA+Boruta算法
输入:数据集D,特征集合F={fi|i=1,2,…,v}
输出:最优特征子集S.
第1步:在数据集D上计算特征fi的综合评估值ci,对特征进行降序排序,删除无关特征,剩余作为候选特征的特征集Scan.
第2步:从数据集D中取出特征集Scan对应的数据作为新的数据集Dnew;假设数据集Dnew为m行n列,即有m组样本,n个特征,其中m>1,n>1,将数据集Dnew复制得到复制特征样本Dcopy.
第3步:将复制特征样本Dcopy按照比例p(0≤p≤1)提取出(m*p)*n组样本,进行随机行变换后放回得到阴影特征样本Ds.
第4步:将原始样本Dnew与阴影特征样本Ds合并,得到一个m行2n列的扩展特征样本集E,采用评判特征重要性措施(平均减少精度)——即Z值,用来评估每个特征的重要性.在E上运行随机森林分类器并不断收集计算的Z值,Z值越高则意味着该特征对于预测结果贡献越大.
第5步:找出阴影特征中得分最大Z值.在每次迭代中,检查一个真实特征的Z值,将特征得分高于最大阴影特征得分的真实特征视为“重要”,将特征得分显著小于最大阴影特征得分的真实特征视为“不重要”,并不断从特征集合中永久删除不重要的特征.
第6步:重复上述步骤,算法达到规定的迭代次数k时停止.
第7步:返回最优特征子集S.
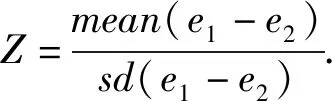
2.3 CEA+Boruta算法时间复杂度分析
本文算法的时间开销主要体现在CEA和Boruta两个阶段.
假设训练数据集的特征维数是m,训练样本个数为n,在CEA阶段,快速排序的平均时间复杂度为O(m(log(m))),随机森林(random forest,RF)学习算法中基分类器的个数为k,则RF算法时间复杂度近似为O(kmn(log(n))2),所以CEA算法的最大渐进时间复杂度为O(3m+kmn(log(n))2).在Boruta阶段,传统的Boruta算法样本复杂度为是O(n!)m,而在改进的Boruta算法中,只有(n*p)*m维的数据对每一列进行了随机行变换,所以该样本集的时间复杂度为O(((n*p)!)m),本算法中p的取值为0.5,两个时间复杂度通过取对数比较可知改进的Boruta算法明显降低了时间复杂度.因此CEA+Boruta算法的最大时间复杂度表示为:
O(m(log(m)))+O(3m+kmn(log(n))2)+O(((n*p)!)m)=O(m*((log(m))+kn(log(n))2+3)+((n*p)!)m).
可以看出,在过滤阶段本文算法时间复杂度与特征维数的平方成正比,这个过程较快的处理了样本数据中冗余的特征,对高维数据具有较好的扩展性,为封装阶段降低了时间开销,提高了随机森林分类器处理重要特征属性的效率和泛化能力.
3 试验及结果分析
3.1 试验数据集
本文试验中,采用的计算机配置为双核,内存16 G,处理器为i7-5820K,选择了3个来自UCI机器学习库公开数据集进行测试(如表1所示),使用python3.7在Jupyter Notebook应用程序上实现算法,分析了本文CEA+Boruta算法相比于Boruta算法和FSIGR算法的优点和不足.
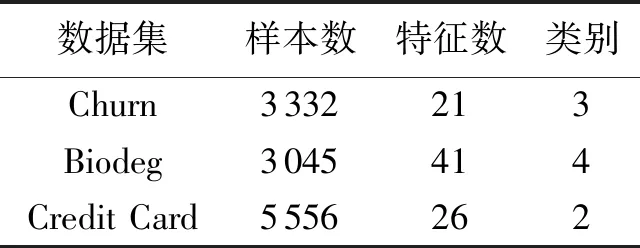
表1 试验数据集Tab.1 Experimental data set
3.2 评价方法和标准
为验证各个算法在随机森林分类器上的效果,实验采用十折交叉验证求取运行效果,以减小误差,每个数据集随机分为10个子集,取其中一个作为测试集,连续运行10次,最后取10次试验结果的平均值作为运行1次所得到的取值[20],改进的Boruta算法阶段取p值取0.5.
本试验使用的评价标准如下:
1) 所选择的特征维数;
2) 各个数据集在不同特征选择算法运行的时间和平均分类错误率;
3) 各个数据集在不同特征选择算法中的精确率P、召回率R与综合评估值F.其计算公式分别为:
其中NTP表示正确分类为正例的数量,NFP表示被错误分类为正例的数量,NTN表示正确分类为反例的数量,NFN表示被错误分类为反例的数量.
3.3 试验结果对比与分析
针对3个数据集,本文通过CEA+Boruta、FSIGR和Boruta 3个模型分别对数据集进行了验证,选取的平均特征维数结果如表2所示.
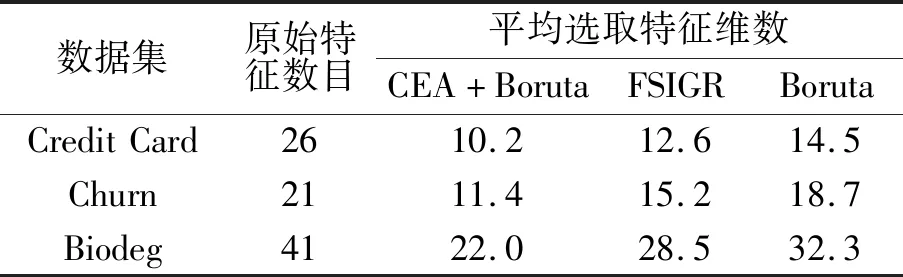
表2 三种方法选取特征维数Tab.2 The feature dimension selected by the three methods
为了验证CEA+Boruta算法的有效性,分别独立使用FSIGR算法和传统的Boruta算法进行对比,从表2可以看出,CEA+Boruta算法同FSIGR算法和Boruta算法相比,3个数据集上均表明CEA+Boruta算法所选出特征子集的数目要少于FSIGR算法和Boruta算法所选的数目.以特征数目较多的数据集Biodeg(特征数目为41)为例,CEA+Boruta算法选出特征数目的平均值为22.0,而FSIGR算法和Boruta算法选出特征数目的平均值分别为28.5和32.3.可以得出,CEA+Boruta算法相比FSIGR算法和Boruta算法,选出特征子集的数目最少,有效降低了特征维数.
传统的特征选择算法通常将特征重要性排序作为结果比较,这样耗时且选择的特征集意义不大,因此本文采取如下方式对几种算法进行了对比,通过CEA+Boruta算法与传统的Boruta算法和FSIGR算法建立模型,在不同的数据集上观察选择出同样维数的特征所需运行的时间、平均分类错误率,如表3所示.
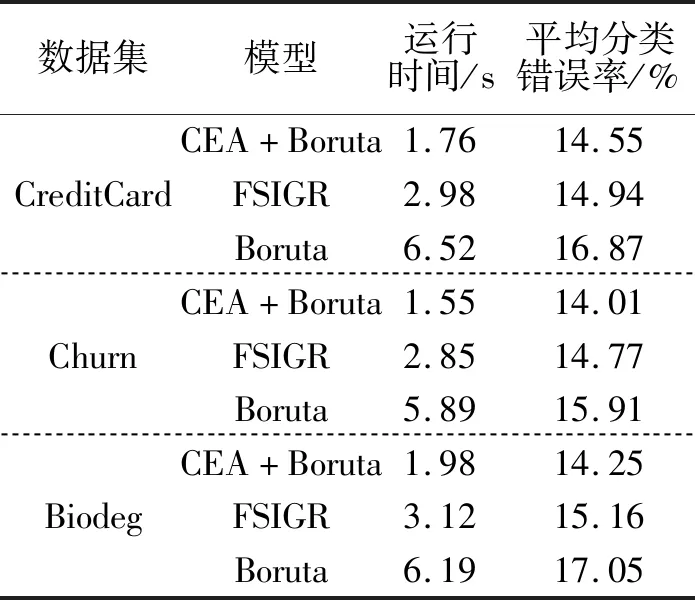
表3 三种方法在不同数据集上运行结果Tab.3 The results of the three methods running on different data sets
从表3可以看出,CEA+Boruta算法和FSIGR算法相比传统的Boruta算法的运行时间和平均分类错误率明显减小.对于特征数目相对较少的CreditCard和Churn数据集来说,CEA+Boruta和FSIGR算法在平均分类错误率差别不大,但是CEA+Boruta算法明显比FSIGR算法运行时间短,可以看出本文提出的算法在特征选择应用上明显缩短了运行时间.而对于特征数目为41的Biodeg数据集,可以看出CEA+Boruta算法在各个方面明显优于其他两种,这说明本文提出的算法降低了计算时间开销,提高了分类准确率.
图1~图3统计了不同数据集中3种算法在平均召回率、平均精确率和平均F值评价指标方面的结果.通过对比可以发现,CEA+Boruta方法比其他两种算法的平均综合评估F值高出至少4%,分类效果明显优于FSIGR和Boruta方法,对于样本最多的CreditCard数据集来说,因类别只有两种,且特征维数不多,所以在随机森林分类器上的平均F值达到最大.数据集Biodeg的原始特征维数是41,几乎是数据集Churn维数的2倍,但和数据集Churn的样本数相差不大,经运行后发现在数据集Biodeg中,3种算法的R、P和F值都比在数据集Churn上高,因此,本文算法在维数较高,类别较少的数据集上分类效果更好.
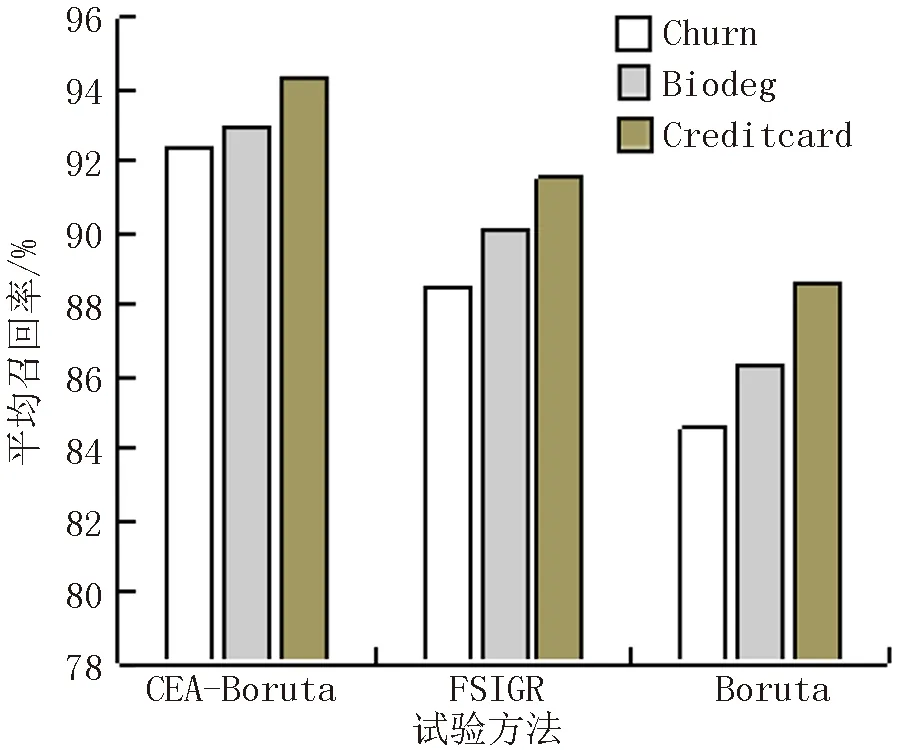
图1 三种方法在不同数据集上平均召回率比较Fig.1 Comparison of the average recall rate of the three methods on different data sets

图2 三种方法在不同数据集上平均精确率比较 图3三种方法在不同数据集上平均F值比较
4 结语
特征选择是预测模型中一个重要步骤,与传统的特征选择算法相比,Boruta算法不必调整太多参数,就能找到候选特征中与类别相关的所有特征,适用于变量较多的数据集,且易于操作和解释.本文介绍了传统的Boruta和CEA算法,并提出了一种新的基于CEA和改进的Boruta特征选择两步法.该算法通过过滤和封装两个阶段以提高算法的性能,同时避免出现过拟合和时间复杂度较高等问题.3个数据集上的实验结果均表明,该算法与FSIGR算法和传统的Boruta算法相比能获得较优的特征集,而且提高运行效率的同时取得了较高的F值.因此,本文提出的特征选择算法相比传统的Boruta算法得到了明显的改进,具有一定的竞争优势,但是本实验中数据集涉及领域不够广泛,如何在不同领域验证Boruta算法阶段最优参数P值是下一步的研究方向.

