G-度量空间中一类满足公共(E.A)性质的新型压缩映象的公共不动点定理

林亚磊，谷 峰

(杭州师范大学理学院，浙江 杭州 311121)

1 引言和预备知识

自2006年Mustafa 和Sime[1]提出G-度量空间的概念以来,G-度量空间中的不动点理论得到了迅猛的发展,人们获得了许多重要的研究成果[2-10].2013年,谷峰和尹云[11]在G-度量空间中引入了映象对满足公共(E.A)性质的概念,并证明了一些新的公共不动点定理.此后,Gu和Shatanawi[12]、郑慧慧,沈云娟和谷峰等[13]、Gu,Shen和Wang[14]、许志鹏和谷峰[15]以及胡品和谷峰[16]等使用公共(E.A)性质和弱相容映象的概念,证明了一些新的公共不动点定理. 本文作为文献[11-16]的一个继续,在G-度量空间的框架下,证明了3对自映象的一个满足新型压缩条件的公共不动点定理. 在文章的最后,还给出了一个支持新结果的实际例子.

由于本文结果中仅要求3对自映象都满足弱相容条件,其中的2对满足公共(E.A)性质,并且对空间的完备性和映象的连续性均不作要求.因而,我们的结果本质地拓广了当前文献中的某些已知结果.

定义1[1]设X是一非空集合,若G:X×X×X→[0,),满足：

(1)G(x,y,z)=0⟺x=y=z；

(2)∀x,y∈X,x≠y,有G(x,y,z)>0；

(3)∀x,y,z∈X,y≠z,有G(x,x,y)≤G(x,y,z)；

(4)G(x,y,z)=G(x,z,y)=G(y,z,x)=G(y,x,z)=G(z,x,y)=G(z,y,x),∀x,y,z∈X；

(5)∀x,y,z,a∈X,有G(x,y,z)≤G(x,a,a)+G(a,y,z).

则称函数G是X上的一个广义度量,简称G是X上的一个G-度量,称(X,G)为广义度量空间或简称为G-度量空间.

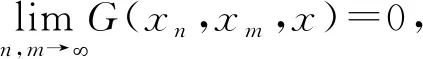
引理1[1]设(X,G)为G-度量空间,则以下叙述相互等价：(1)序列{xn}收敛于x；(2)G(xn,xn,x)→0(n→)；(3)G(xn,x,x)→0(n→)；(4)G(xn,xm,x)→0(n,m→).

定义3[1]设(X,G)为G-度量空间,{xn}⊂X,如果∀ε>0,存在正整数N,使得对于任意的n,m,l≥N,有G(xn,xm,xl)<ε,即G(xn,xm,xl)→0(n,m,l→),则称序列{xn}为Cauchy列.

引理2[1]设(X,G)为G-度量空间,则以下叙述等价：(1)序列{xn}是Cauchy列；(2)∀ε>0,∃N,∀n,m≥N,有G(xn,xm,xm)<ε,或G(xn,xm,xm)→0(n,m,→).

定义4[1]设(X,G)为G-度量空间,如果对于(X,G)上的每个Cauchy列都在X上是收敛的,则称(X,G)为完备的G-度量空间.

定义5[17]设f,g是集合X上的自映象,若w=fx=gx,x∈X,则称x为f,g的一个重合点,并称w为f,g的一个重合像点.

定义6[17]称集合X上的自映象对(f,g)是弱相容的,如果它们在重合点处是可交换的.

定义7[18]设(X,G)为G-度量空间,我们称X上的自映象对(f,g)满足G-(E.A)性质,若∃{xn}⊂X使得{fxn},{gxn}都G收敛于某t(t∈X).

2 主要结果

定理1设(X,G)为G-度量空间,映象f,g,h,R,S,T:X→X满足以下条件：

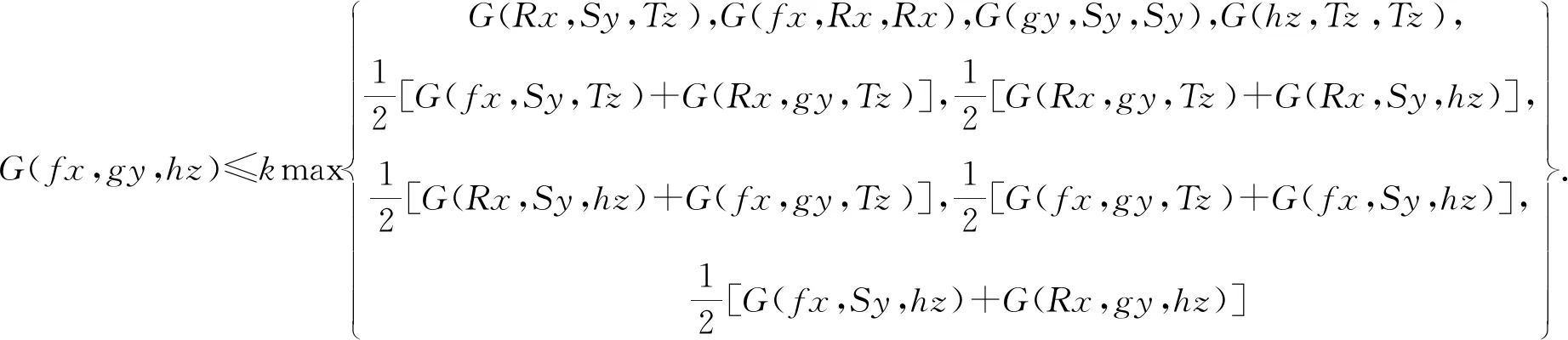
(1)

∀x,y,z∈X.其中常数k∈[0,1).如果满足下列条件之一,则映象对(f,R),(g,S)和(h,T)在X中有公共重合像点.

(i)RX是X中的闭集,fX⊂SX,gX⊂TX,映象对(f,R)和(g,S)满足公共(E.A)性质；

(ii)SX是X中的闭集,gX⊂TX,hX⊂RX,映象对(g,S)和(h,T)满足公共(E.A)性质；

(iii)TX是X中的闭集,fX⊂SX,hX⊂RX,映象对(f,R)和(h,T)满足公共(E.A)性质.

进一步,当3对映象(f,R),(g,S)和(h,T)都弱相容时,f,g,h,R,S和T有唯一公共不动点.

证明假设(i)成立,即RX是X的闭集,fX⊂SX,gX⊂TX,映像对(f，R)和(g，S)满足公共(E.A)性质.由公共(E.A)性质的定义可知,∃{xn},{yn}⊂X和t∈X,使得

(2)

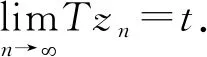
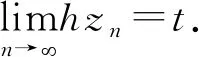
在上式中令n→,使用和式(2)得：

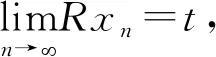
在上式中令n→,得到G(fu,t,t)≤kG(fu,t,t).因为k∈[0,1),所以G(fu,t,t)=0,于是fu=t=Ru,即u是f和R的一个重合点.

因为fX⊂SX,所以∃v∈X,使得fu=Sv=t.再由式(1),可得

在上式中令n→,得到G(t,gv,t)≤kG(t,gv,t).因为k∈[0,1),所以G(t,gv,t)=0,于是gv=t=Sv,即v是g和S的一个重合点.

因为gX⊂TX,所以∃w∈X,使得Tw=gv=t. 利用式(1),得到

注意到fu=Sv=t和Tw=gv=t,则上式变为G(t,t,hw)≤kG(t,t,hw).因为k∈[0,1),所以G(t,t,hw)=0,于是hw=t=Tw,即w是h和T的一个重合点.

综上,我们证明了当条件(i)成立时,有fu=Ru=gv=Sv=hw=Tw=t.即t是映象对(f,R),(g,S)和(h,T)在X中的一个公共重合像点.

同理,如果满足条件(ii)或(iii),证明过程与上述步骤类似,可得到同样的结论.

进一步,如果映象对(f,R),(g,S)和(h,T)都是弱相容的,则由

ft=fRu=Rfu=Rt,gt=gSv=Sgv=St,ht=hTw=Thw=Tt.

(3)

在式(1)中取x=t,y=v,z=w,并利用式(3)得到

G(ft,t,t)=G(ft,gv,hw)≤

kG(ft,t,t).

因为k∈[0,1),所以G(ft,t,t)=0,故ft=t,进而有ft=t=Rt.

同理可证得,gt=St=t,ht=Tt=t.所以t是f,g,h,R,S和T的一个公共不动点.

下证公共不动点t是唯一的.事实上,假设p∈X是f,g,h,R,S和T的另一个公共不动点,在式(1)中取x=p,y=z=t,则得到

G(p,t,t)=G(fp,gt,ht)≤

kG(p,t,t).

因为k∈[0,1),所以G(p,t,t)=0,即t=p.于是公共不动点t是唯一的.

下面的例子表明定理1是有效的.

例1设X=[0,1],定义为G(x,y,z)=|x-y|+|y-z|+|z-x|, 则(X,G)是一个G-度量空间. 定义X上的自映象f,g,h,R,S和T分别为

则显然f,g,h,R,S和T都是不连续映象,且RX是X中的闭集,fX⊂SX,gX⊂TX,hX⊂RX,映象对(f,R),(g,S)和(h,T)都是弱相容的.

我们分8种情况予以证明.

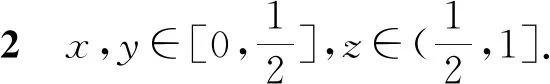
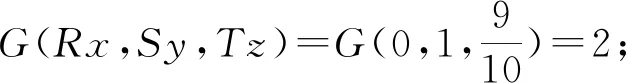
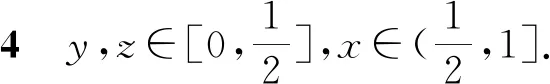
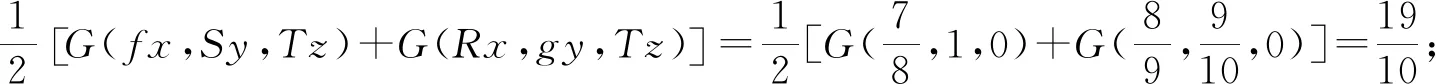
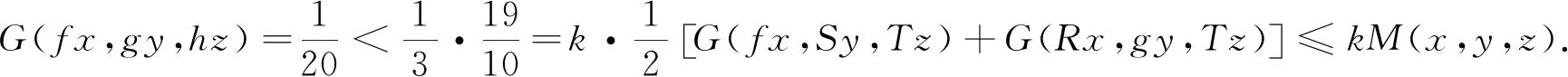
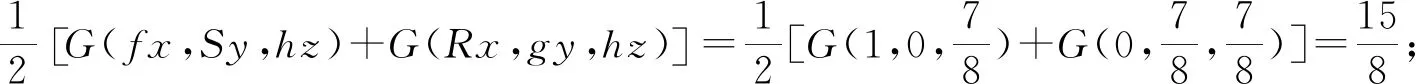
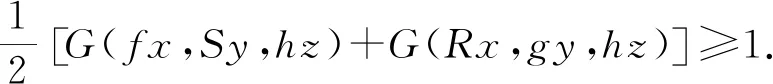
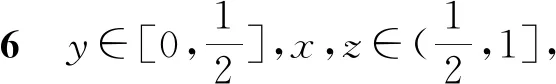
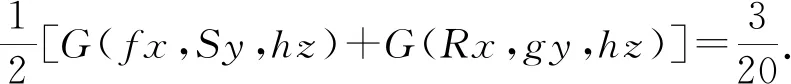
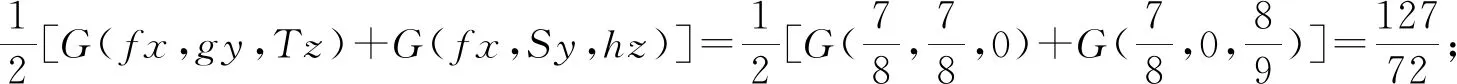
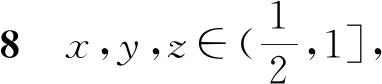
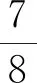
推论1设(X,G)为G-度量空间,映象f,g,h,R,S,T:X→X满足以下条件：

G(fx,gy,hz)≤a1G(Rx,Sy,Tz)+a2G(fx,Rx,Rx)+a3G(gy,Sy,Sy)+a4G(hz,Tz,Tz)+

a5[G(fx,Sy,Tz)+G(Rx,gy,Tz)]+a6[G(Rx,gy,Tz)+G(Rx,Sy,hz)]+

a7[G(Rx,Sy,hz)+G(fx,gy,Tz)]+a8[G(fx,gy,Tz)+G(fx,Sy,hz)]+

a9[G(fx,Sy,hz)+G(Rx,gy,hz)]

∀x,y,z∈X.其中常数ai≥0(i=1,2,3,4,5,6,7,8,9),满足

a1+a2+a3+a4+2(a5+a6+a7+a8+a9)<1.

如果下列条件之一被满足,则映象对(f,R),(g,S)和(h,T)在X中有公共重合像点.

(i)RX是X中的闭集,fX⊂SX,gX⊂TX,映象对(f,R)和(g,S)满足公共(E.A)性质；

(ii)SX是X中的闭集,gX⊂TX,hX⊂RX,映象对(g,S)和(h,T)满足公共(E.A)性质；

(iii)TX是X中的闭集,fX⊂SX,hX⊂RX,映象对(f,R)和(h,T)满足公共(E.A)性质.

进一步,当3对映象(f,R),(g,S)和(h,T)都弱相容时,f,g,h,R,S和T有唯一公共不动点.

则

G(fx,gy,hz)≤a1G(Rx,Sy,Tz)+a2G(fx,Rx,Rx)+a3G(gy,Sy,Sy)+a4G(hz,Tz,Tz)+

a5[G(fx,Sy,Tz)+G(Rx,gy,Tz)]+a6[G(Rx,gy,Tz)+G(Rx,Sy,hz)]+

a7[G(Rx,Sy,hz)+G(fx,gy,Tz)]+a8[G(fx,gy,Tz)+G(fx,Sy,hz)]+

a9[G(fx,Sy,hz)+G(Rx,gy,hz)]≤[a1+a2+a3+a4+2(a5+a6+a7+a8+a9)]M(x,y,z).

令k=a1+a2+a3+a4+2(a5+a6+a7+a8+a9),则由已知条件知k∈[0,1).由定理1即得推论1成立.

注1 推论1中,在a1,a2,a3,a4,a5,a6,a7,a8,a9这9个数中取其中 1个、2个、…、8个数为0,则可得出一系列推论,限于篇幅省略.

注2 本文所得结果都是新的,与当前已有结果不同.