基于图嵌入法的时序网络链路预测研究

吴晨程，周银座

(杭州师范大学阿里巴巴商学院，浙江 杭州 311121)

0 引言

当下，复杂网络这一新兴的交叉学科被越来越多的人作为分析手段来对现实世界进行数据挖掘[1-2].在复杂网络理论中，链路预测[3]的方法对于还原网络中缺失的信息以及挖掘网络中潜在的结构显示出巨大的威力.

链路预测的传统方法是基于机器学习[4]，这种解决思路是将链路预测看作机器学习中的分类问题，根据每一对节点之间的特征，将节点对分为正例和反例，即有连边和无连边.这种分类问题过度依赖网络中的节点属性，而节点的属性值既难以获取且无法保证其可靠性.由于以上弊端，基于节点相似性的链路预测算法得以发展，即两个节点的相似性越大，它们之间存在边的可能性就越大.基于节点相似性的链路预测算法主要有3类：基于局部信息的相似性指标[2,5-7]、基于路径的相似性指标[7-9]、基于随机游走的相似性指标[10-13].基于局部信息的相似性指标是指通过节点的局部信息(节点的度、共同邻居数量等)计算得到的相似性指标，其计算复杂度较低，但代价是预测效果的相对降低.基于路径的相似性指标是指利用要预测的两个节点之间的路径信息(节点之间的路径数量、路径中间节点的信息等)计算得到的相似度指标，该类指标在计算多阶路径信息的贡献时，计算复杂度较高.基于随机游走的相似性指标是基于随机游走过程定义的，即假设一个粒子从某个初始节点出发，以一定的概率随机游走到它的邻居节点，然后继续扩散，直到该粒子处在所有节点上的概率达到稳定.这类指标很好地考虑到了网络的全局信息，在推荐系统和社团发现中也有很好的应用.

研究发现在链路预测算法中，粒子随机游走的转移概率仅仅取决于当前节点的度信息，而不关心其邻居节点的网络拓扑结构特征，从而粒子下一时刻从当前节点转移到任意邻居节点的概率是相同的，具有较强的随机性.然而真实的网络结构复杂多样，粒子在随机游走的过程中不一定是按照等概率的方式转移，而应该是一种有偏向的转移，即粒子会倾向于从当前节点转移到与当前节点更相似的邻居节点上.基于节点拓扑结构相似性的有偏向随机游走，理论上应该比具有强随机性的随机游走有更高的效率，对算法有更好的提升.

在链路预测的具体计算过程中，通常将网络表示成邻接矩阵进行存储.这对于大型的网络是一个不小的负担.为了使这个方法能够更有效地应用到大型网络中，研究使用了图嵌入方法[14](Graph Embedding Method，GEM).该方法是将图数据或者高维稠密的矩阵映射为低维稠密向量的方法，同时使原网络中属性接近或拓扑结构相似的节点在向量空间上的位置也接近.这样，通过降维的方法大大降低了计算的复杂度.例如，Mikolov等[15]在文献中提出的Word2Vec神经网络语言模型在词表示上取得了良好效果，Perozzi[16]在此基础上提出DeepWalk算法，引入了深度学习，利用随机游走采样得到的节点序列类比于“句子”，将节点类比于“词”，使用Word2Vec模型获得节点表示向量，在网络分析任务中获得了较大的性能提升.随着图嵌入的广泛应用，后来相继出现了基于简单神经网络的LINE[17]，基于DeepWalk改进的Node2Vec[18]，基于空间相似性的Struc2Vec[19]等算法.

链路预测研究的真实网络大多都会随时间而变化，然而为了方便研究有时会将这种动态变化忽略，让算法基于网络的静态特征去预测链路.然而，对于一些网络而言，他们具有复杂的动态结构和非线性的拓扑特征，这意味着有些链路会在下一时刻突然消失或出现[20].这种特性被称为“时序性”.对于这类网络，不仅要观察网络的拓扑特征，还要将时序性考虑进去.在较早的研究中，已经有研究者对基于时序网络的链路预测做了研究和总结.Sarkar P[21]等人基于节点特征及节点周围领域特征提出了一种非参数化的时序网络链路预测方法.Butun E[22]等人提出基于邻居和图模式的拓扑指标方法，并应用于有向、加权、时序的复杂网络场景，有较好的性能表现.Hyoungshick Kim[23]等人使用了度中心性来预测未来网络中重要的节点.Catherine A. Bliss[24]等人整合网络节点属性信息和网络拓扑结构特征并提出了一种进化算法来提高链路预测的精确度.

基于上述问题和研究现状，研究认为在现实网络尤其是时序网络中，使用随机游走方式进行链路预测时，粒子转移会受到网络结构和时间推移的影响从而进行有偏向的转移，这种转移方式具有较高的准确性，可以更好地考虑全局信息.本文基于以上分析，提出了一种基于图嵌入法的时序网络重启随机游走算法，通过实验验证此算法在时序网络环境下有优秀的预测精度，较传统基准方法有较大的性能提升.

1 相关工作

本部分将介绍链路预测中经典的基准指标、常见的图嵌入算法以及链路预测的评价指标.

1.1 链路预测经典指标

1)共同邻居(Common Neighbors，CN)[5]

对于网络中的节点x，定义其邻居集合为Γ(x)，则两个节点x和y的相似性定义为它们共同的邻居数，即：

Sxy=|Γ(x)∩Γ(y)|.

其中wxz表示节点x和y的边权，显然若所有边权都等于1，该指标就等同于无权的CN指标.

2)Adamic-Adar指标(AA)[6]

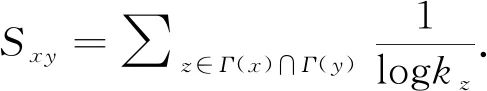
其中sz为节点的强度，强度定义为节点与其邻居节点之间的连边权重和.

3)资源分配(Resource Allocation，RA)[7]

RA指标认为没有直接相连的两个节点x和y，可以通过共同邻居作为传递媒介从而传递资源.假设每个媒介都有一个单位的资源并且将平均分配传给它的邻居，则节点y接收的资源数即节点x和y的相似度，即：

4)偏好连接指标(Preferential Attachment，PA)[2]

在无标度网络结构中，一条新边连接到节点x的概率正比于该节点的度，定义两个节点间的偏好连接相似性为：

Sxy=kxky.

对于加权环境，定义含权的PA指标为：Sxy=∑i∈Γ(x)wix×∑j∈Γ(y)wjy=sxsy.

5)有重启的随机游走指标(Random Walk with Restart, RWR)[13]

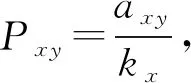
πx(t+1)=α·PTπx(t)+(1-α)ex，

其中ex表示初始状态，上式可以计算出稳态解，公式如下：

πx=(1-α)(I-αPT)-1ex，

其中元素πx表示从节点x出发的粒子走到节点y的最终概率，并由此定义相似性：

1.2 图嵌入方法

1)Word2vec

Word2vec是Google公司在2013年开放的一款用于训练词向量的软件工具，主要包括CBOW模型和Skip-Gram模型.前者通过训练上下文节点来预测中间词，后者则相反，输入中间词从而得到上下文节点.模型是一个包含输入层、投影层、输出层的3层神经网络，如图1所示.

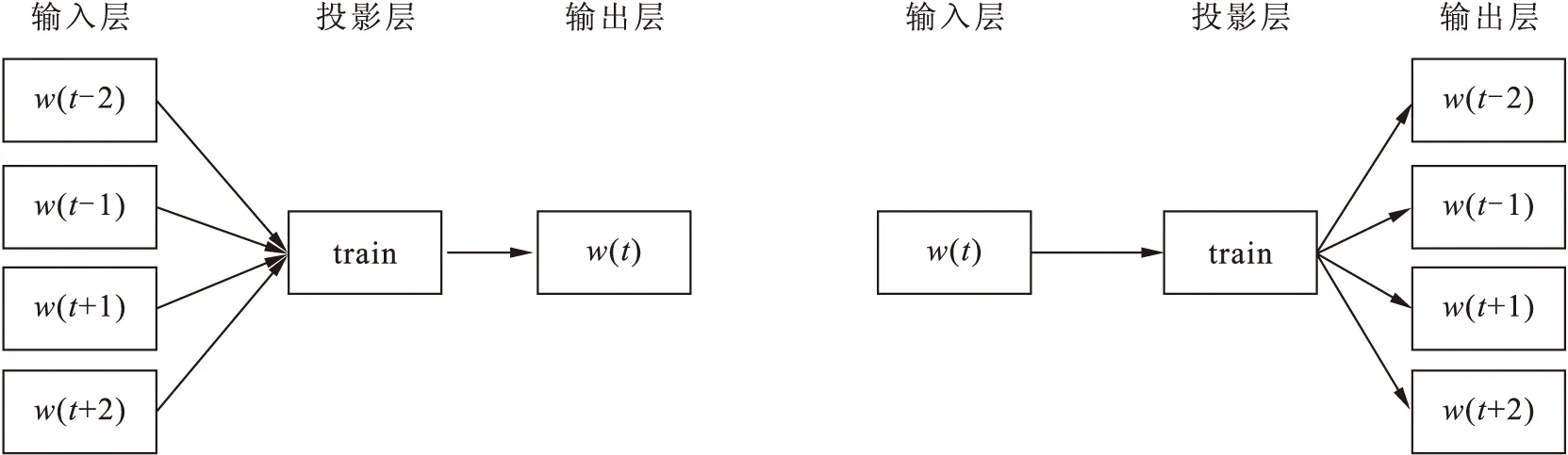
图1 CBOW模型(左)和Skip-Gram模型(右)Fig.1 CBOW model (the left) and Skip-Gram model (the left)

图嵌入方法正是通过采集网络的节点构成节点序列，将节点序列类比成“句子”，使用Word2vec模型生成得到节点向量(相当于“词”).通过这种方式得到的节点向量.因为考虑了节点的上下文信息，因此对于网络分析任务有较大的性能提升.

2)Node2vec

Node2vec是一种经典的图嵌入方法，它通过随机游走方式采集节点序列，并结合了深度优先遍历(DFS)和广度优先遍历(BFS)，可以更好地获取网络的全局信息.Node2vec的随机游走策略为，给定当前顶点v，访问下一个顶点x的概率为：

其中πvx是顶点v和顶点x之间未归一化的转移概率，Z为归一化常数.

Node2vec引入两个超参数p，q来控制随机游走策略.假设当前随机游走经过边(t,v)到达节点v时，设πvx=αpq(t,x)·wuv,其中wuv是顶点v和x之间的权值：

其中dtx为顶点t和顶点x之间的最短距离.参数p是控制重复访问刚刚访问过的顶点概率，dtx=0表示顶点t就是刚刚访问过的顶点x，若p值较高，则重复访问的概率将会降低.参数q是控制游走向内还是向外的概率，若q>1，随机游走偏向于访问跟节点t相近的节点(BFS)，若q<1，随机游走偏向于访问远离节点t的节点(DFS).

1.3 评价指标

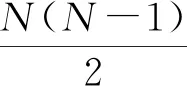
AUC(area under the receiver operating characteristic curve)[25]是衡量链路预测算法精确度最常用的指标.它是指在测试集中随机选择一条边的分数值比随机选择的一条不存在的边分数值高的概率.实验时，每次随机从测试集中选取一条边，再从不存在的边中随机选择一条，如果测试集中的边分数值大于不存在的边的分数值，那么就加1分，如果两个分数值相等就加0.5分.这样独立比较n次，如果有n′次测试集中的边分数值大于不存在的边分数，有n″次两分数值相等，那么AUC指标的定义为：

一般的，AUC越接近1，算法的精确度越高.

在时序网络的链路预测计算中，移动窗口切片方法是选取训练集和测试集的一种方式.首先将时序网络按照等量的时间间隔划分为若干个时间切片.假定设置时间窗口大小为T，选取前T个时间切片作为训练集，第T+1时刻的时间切片作为测试集，计算得到一次AUC.接着将时间窗口移动一个单位，再计算得到AUC.当时间窗口到达最后一个切片为止，我们就得到了基于此时间窗口大小的每一次独立的实验的AUC，取平均值作为对应时间窗口大小T的AUC.

2 基于图嵌入法的时序网络链路预测算法

本部分将介绍一种基于图嵌入法的时序链路预测算法.该方法针对RWR指标中随机游走的强随机性问题做了改进，并引入了基于节点间拓扑结构相似性的有偏向的转移概率.下文将详细叙述如何使用图嵌入法计算得到这种转移概率并如何改进原有的链路预测算法.

2.1 基于图嵌入法的重启随机游走

图嵌入法的核心思想是训练节点序列，生成低维的节点向量.节点序列的采集受不同图嵌入算法的定义而有所不同，可以根据具体的网络信息选择合适的图嵌入算法.而节点向量的训练过程综合考虑了节点的“上下文信息”，即通过深度学习不断训练节点的网络结构特征从而获得最优的向量表示，因此节点在向量空间上的相似性可以很好地表征节点在网络结构上的相似性.

本文以Node2vce为例，采集节点序列生成得到节点向量.定义任意节点x的向量表示为Φ(x)=[x1,x2,…,xd]，任意节点y的向量表示为Φ(y)=[y1,y2,…,yd]，考虑节点间的边权后使用通用的余弦相似度指标可以量化两个节点向量在向量空间上的相似程度，同时也可以表示节点在网络结构上的拓扑结构相似性，给出定义1.

定义1网络中任一节点x和节点y的潜在拓扑结构相似性为：

其中余弦值越接近1，就表明夹角越接近0度，也就是两个向量越相似，在网络结构上两个节点越相似.wxy为节点x和节点y之间的边权，在无权网络环境下表示的是两节点是否相连，相连为1，反之为0.

因为RWR指标的随机游走转移概率仅考虑节点的度信息而不关心节点的潜在拓扑结构特征，所以本文将定义1中计算得到的节点拓扑结构相似性加入随机游走过程中，给出定义2的基于图嵌入法模型的有偏向的随机游走转移概率.

定义2任意节点x与其任意邻居节点y的转移概率为：

其中A∈(0,1)，表示动力系数，即控制粒子随机游走的动力，决定当前时刻是否进行随机游走,从结果上看也决定了粒子随机游走的范围.当A=1时，粒子一直保持随机游走动力，每次游走都将选择当前节点的一个邻居节点作为下一个游走目标，会尽可能地考虑全局信息；随着A的值不断缩小，粒子会更倾向于保持原地，进行相对局部的游走；当A=0时，粒子将永久停留在原地，这种情况是不符合常理的，这里仅作为参数的边界.N(x)为节点x的邻居节点集合，∑z∈N(x)CosSim(x,z)是归一化因子.

2.2 时序网络下的转移概率

定义1和定义2都是基于静态网络环境下的定义，而现实网络有很多是动态变化的.如果这种动态变化的规律可以被算法识别，那么就可以有效提高预测结果的精确度.

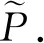
定义3给定时间窗口大小T的全局时序网络随机游走概率为：

其中，γ∈(0,1)表示阻尼因子，Pt表示当前时刻下的粒子有偏向转移概率.

2.3 算法流程

本文提出的算法主要改进的是RWR指标的转移概率，算法的主要原理同RWR，即通过引入重启因子α进行随机游走从而捕捉网络的全局信息，进而预测网络的链路.因为使用了图嵌入方法计算有偏向转移概率并基于时序网络应用，因此该算法被命名为基于图嵌入法的时序网络重启随机游走算法(Graph Embedding Temporal Random Walk with Restart，GETRWR)，其主要流程如下：

输入：时序网络G(V,Et,At)(t=t0,t0+1,…,t0+T-1)，重启因子α∈(0,1)，动力系数A∈(0,1)，阻尼因子γ∈(0,1).

输出：时序网络相似性矩阵S.

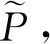
②根据定义2计算每一时刻下的节点间转移概率并更新Pt;

④Fori=1 tondo；

⑤WhileS不收敛 do；

⑥πx=(1-α)(I-αPT)-1ex;

⑦End While;

⑧End For;

⑨ReturnS.

3 实验结果与分析

在本部分将使用真实网络数据集对以上算法进行实验验证，并使用经典的基准指标做性能对比.

3.1 实验数据

Email：一家中型制造业企业员工间的邮件交流(2010.1.3—2010.10.1)；

FB：Facebook用户间的论坛交互(2004.5.15—2004.10.26).

实验数据是典型的时序网络，其中节点与连边随时间变化而变化，网络信息见表1.

表1 网络的基本信息Tab.1 Basic information about the network

3.2 实验结果与分析

根据实验数据的时间跨度，按周为单位将数据集划分为合适数量的时间切片，其中Email的时间切片数量为38个，FB的时间切片数量为22个.

3.2.1 预测结果

设置时间窗口T=10，动力系数A=0.1，阻尼因子γ=0.5，选择经典的链路预测指标CN、AA、RA、PA、RWR作为基准指标，选择AUC作为评价指标.其中对于基准指标使用时序网络的计算方法，即将历史信息作为训练集，当前时刻的网络作为测试集.实验结果如表2所示.

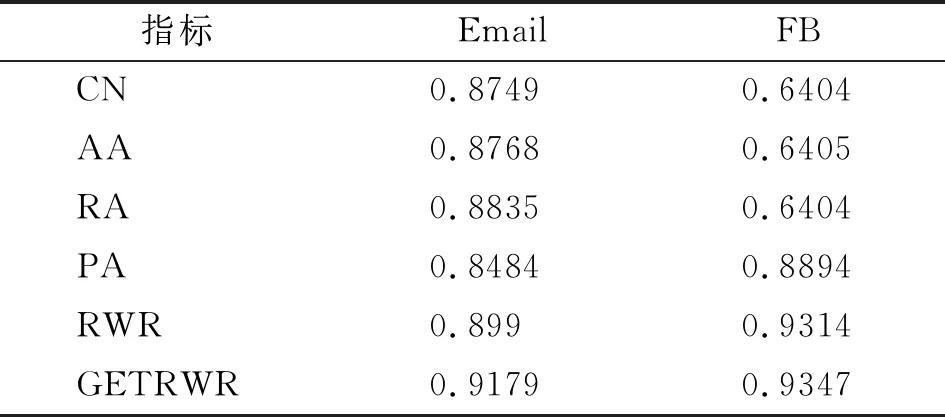
表2 GETRWR与其他指标的预测效果(AUC)Tab.2 The predictive effect of GETRWR and other indicators

从整体上看，GETRWR表现符合预期，具有最优的性能表现，预测准确率最高.其中对于RWR指标有明显提升，尤其在Email数据集上预测效果提升了1.89%，说明有偏向的转移在时序网络中起到了积极作用.此外，在时序网络中时间窗口的大小是非常重要的一个参数，其次动力系数和阻尼因子这两个算法中的参数也对实验结果有影响，因此分别对这3个参数控制变量进行实验，观察实验结果.

3.2.2 时间窗口的影响

设置时间窗口大小T为变量，固定动力系数A=0.1，阻尼因子γ=0.5，实验的AUC值随时间窗口大小变化的趋势如图2所示.

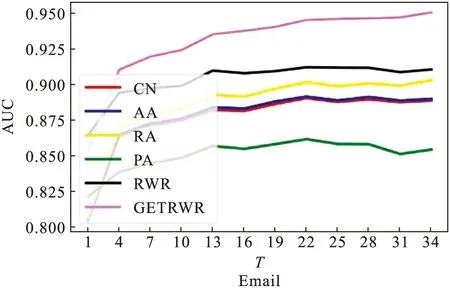
当时间窗口T=1时，相当于预测模型仅使用前一时刻的网络信息进行训练，因为包含的历史信息过少从而预测效果最差.随着时间窗口T的不断增加，预测结果也随之增长，这是因为时序网络的节点信息变化较快，必须参考一定数量的历史信息才能训练好时序模型，而获取了一定数量的历史信息后，预测结果会呈现一种稳定的状态，不会因为急需增加历史信息而明显变化.由图可见，当T>10时，算法的预测效果趋于平稳.值得注意的是，GETRWR较RWR指标，除了T较小的情况外，预测效果均占优势，同样说明了粒子在随机游走中的有偏向转移的重要性.此外，实验发现CN、AA、RA在实验数据集上的表现接近，说明了在这一类数据中，基于共同邻居和惩罚大度节点的效果接近.

3.2.3 动力系数的影响

设置动力系数A为变量，固定时间窗口T=10，阻尼因子γ=0.5，实验结果AUC随动力系数变化的趋势如图3所示.

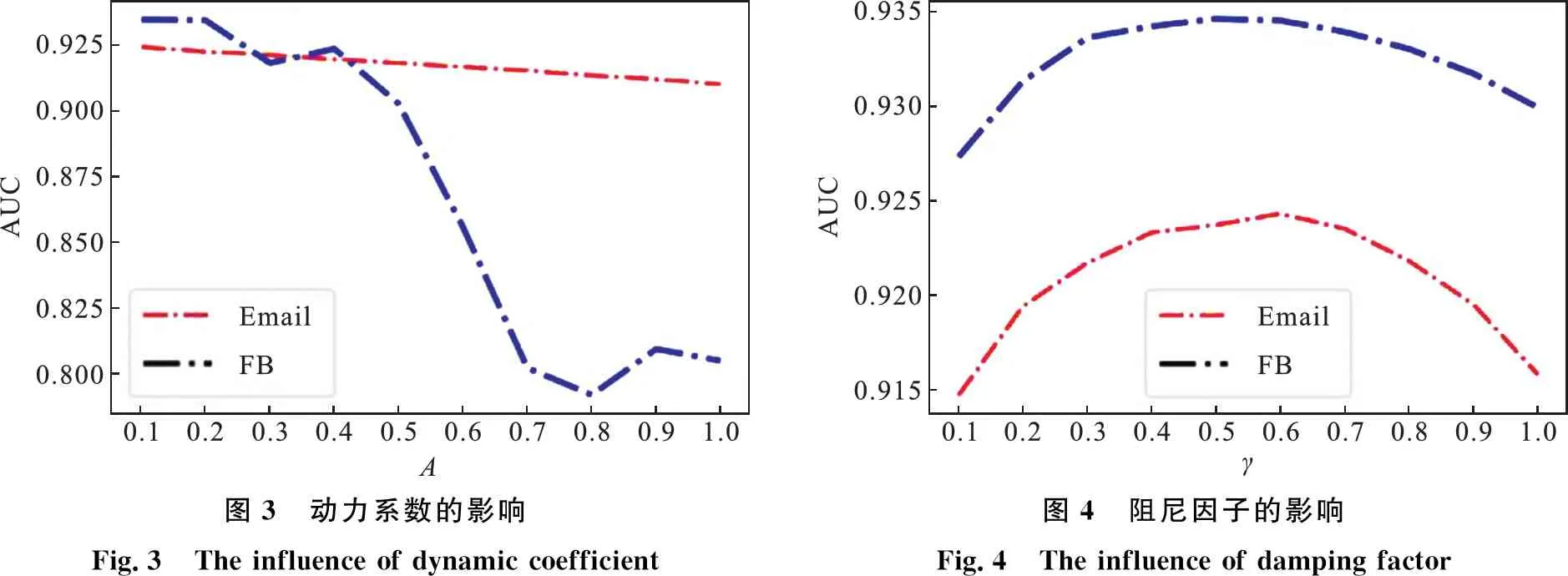
图3 动力系数的影响Fig.3 The influence of dynamic coefficient图4 阻尼因子的影响Fig.4 The influence of damping factor

对于不同的数据集，动力系数的最优值也有所不同，对于本文选取的两个网络，动力系数的最优值出现在0.1～0.3之间，这和具体的网络结构有关，说明对于这类特征的网络，粒子进行局部随机游走的效果会更好.GETRWR算法中动力系数的大小对预测精度有较大的影响，因此可以通过实验调参获取最佳的动力系数.

3.2.4 阻尼因子的影响

设置阻尼因子γ为变量，固定时间窗口T=10，动力系数A=0.1，实验结果AUC随阻尼因子变化的趋势如图4所示.

根据上文定义3的公式可知，当γ=1时，GETRWR在计算转移概率时平等看待了所有的历史时间切片，即最远和最近的时间切片有相同的权重，这样导致过于久远的历史信息对预测产生了干扰影响.而当γ过小时，历史信息所占权重很低，从而导致预测效果不佳.图4的结果也证明了当γ处于0.4～0.6之间时，算法的性能最高，说明了较为久远的历史信息虽然可能对预测结果带来“误导”，但也不可完全忽视.GETRWR算法中阻尼因子的大小对预测精度有较大的影响，因此对于实验结果可以通过调参找到最佳的阻尼因子.

4 结论

时序网络是链路预测研究中的一个重点，因为其特有的“时序性”，导致了常用的基于静态网络的方法不再高效适用.本文提出了一种新的时序网络链路预测算法(GETRWR)，其中改进了链路预测中粒子随机游走的传统转移方式，即定义了考虑节点拓扑结构相似性后的有偏向转移.研究使用图嵌入法训练节点序列生成节点向量，可以从低维的向量空间上比较节点的拓扑结构特征，基于此计算粒子在随机游走过程中的有偏向转移，并替换RWR中的转移概率.此外，针对时序网络的时序性特点，考虑历史信息的影响，对于不同时刻的时间切片赋予不同的权重，将不同时刻下的粒子转移概率融合成全局的转移概率，基于这种转移概率应用的时序网络链路预测算法有较高的性能表现，较基准指标有较大的提升.在下一步的研究中，会考虑有向网络的情况，并比对更多的时序网络数据集和现有的时序网络链路预测方法.