一道含参模考题求解的多角度思考

马进才 王 建 李 萌

河北省邯郸市第一中学 (056002)

题目已知函数f(x)=(x+1)[ln(x+1)+m]+n，曲线y=f(x)在点(0,f(0))处的切线方程为y=2x+1.

(1)求m,n的值和f(x)的单调区间；

(2)若对任意的x∈[0,+∞),f(x)>kx恒成立，求整数k的最大值.

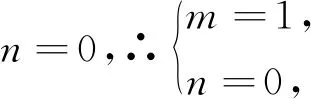
(2)法一：(分类讨论)由(1)可知f(x)=(x+1)[ln(x+1)+1]，对∀x∈[0,+∞),f(x)>kx恒成立，即f(x)-kx>0恒成立.令g(x)=f(x)-kx=(x+1)[ln(x+1)+1]-kx，只需g(x)min>0，则g′(x)=ln(x+1)+2-k≥2-k.

①当k≤2时g′(x)≥0恒成立(当且仅当x=0,k=2时取等号)，此时g(x)在[0,+∞)单调递增，g(x)≥g(0)=1满足.

②当k>2时，令g′(x)=0,得x=ek-2-1，当x∈(0,ek-2-1),g′(x)<0,g(x)单调递减；当x∈(ek-2-1,+∞),g′(x)>0,g(x)单调递增，故g(x)min=g(ek-2-1)=ek-2(k-1)-k(ek-2-1)=-ek-2+k，易知-ek-2+k为减函数，当k=3时,

-ek-2+k>0；当k=4时-ek-2+k<0，故当k=3时满足条件.

综上，整数k的最大值值为3.

法二：(参变分离+隐零点虚设根)由题当x=0时满足条件.

法三：(必要性探路)∵f(x)=(x+1)[ln(x+1)+1]≥kx对∀x∈[0,+∞)恒成立，令x=1,即2(ln2+1)≥k,∵ln2≈0.69,k∈Z,∴k≤3.当k=3时，构造g(x)=(x+1)[ln(x+1)+1]-3x，只需证明g(x)min≥0即可，此时k是最大符合要求的整数.g′(x)=[ln(x+1)+1]+1-3=ln(x+1)-1，令g′(x)=0,∴x=e-1,∴g(x)在(0,e-1)单调递减,(e-1,+∞)单调递增,∴g(x)min=g(e-1)=3-e>0,∴kmax=3.