例析多角三角函数极值的求解
2020-09-23 02:00刘凯峰
中学数学研究(江西) 2020年9期
顾 敏 刘凯峰
南通大学理学院 (226007) 南通大学数学师范172班 (226007)
多角三角函数极值问题是高中数学中的一个热点问题.学生求解此类问题时,常常出现想消元消不了,想变形功力又不够,陷入一筹莫展的境地.针对式子的结构特征,我们有时可以尝试利用主元思想,把某个角度当做主变量,其他角度暂时当做常系数.假若式子中既有该角的正弦又有该角的余弦,且是和的形式,那么辅助角法往往能够奏效.并且某些问题通过利用辅助角法可以达到放缩和消元一箭双雕的效果,求解过程往往也用不到多少三角恒等变形技巧,何乐而不为呢!
本文精选几个实例,每例均给出两种不同的解法,旨在说明辅助角法的解题功效.

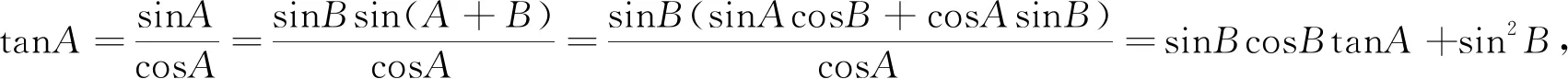


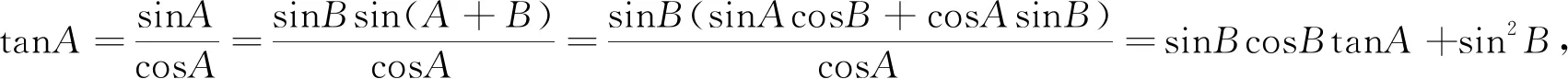
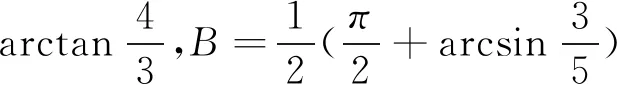

例2 (2018年河南预赛题)已知cos(α+β)=cosα+cosβ,试求cosα的最大值.
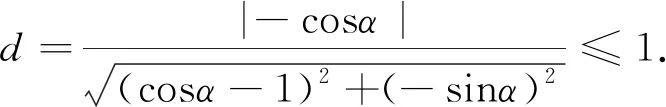
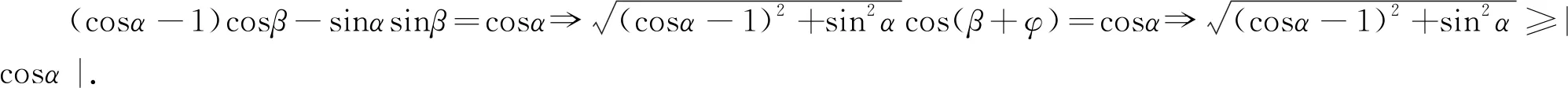
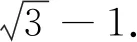
点评:利用解析1设法赋予相关式子几何意义,需要比较强的联想能力.解析2辅助角法比较直接有力.




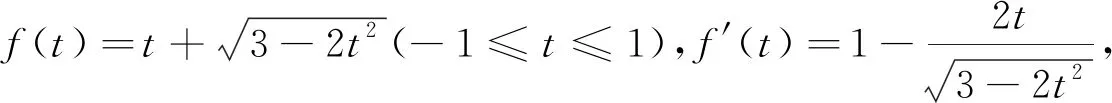
点评:证明1中利用和差化积与积化和差公式,再利用余弦函数有界性进行放缩,进而求极值.证明2则绕过三角恒等变换,比较快速地得到可换元的一元函数,再利用导数求最值.
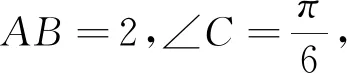
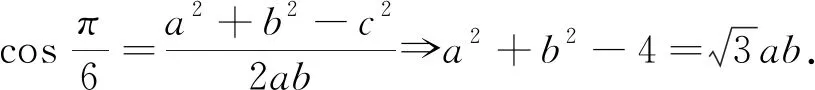


点评:解析1通过余弦定理得到一个2次等式作为条件,所求目标是个1次式,令该1次式为t,现在把t作为常数,设法将2次等式中一个变量消去,利用判别式法求解.解析2通过正弦定理化边为角后,出现了2个角.要是目标式子中只出现1个角,并且既有该角的正弦,又有该角的余弦,进一步还是一个和式,辅助角法当仁不让.
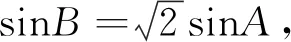
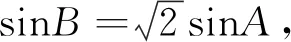
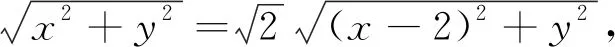

点评:解析1中建系的前提是已知条件蕴含了阿波罗尼斯圆;解析2是主动设元,巧妙地将cosB由已知条件消去,此处辅助角法派上用场.
猜你喜欢
数学小灵通(1-2年级)(2022年10期)2022-10-27
微特电机(2022年1期)2022-02-11
中学生数理化·七年级数学人教版(2020年5期)2020-08-10
小学生学习指导(低年级)(2019年5期)2019-04-29
中学数学杂志(高中版)(2016年6期)2017-03-01
福建中学数学(2016年7期)2016-12-03
中学生数理化·七年级数学人教版(2016年4期)2016-11-19
中学生数理化·七年级数学人教版(2016年4期)2016-11-19
北京信息科技大学学报(自然科学版)(2016年5期)2016-02-27
读写算·小学低年级(2015年9期)2015-09-18

